Waiting lines of people often form at banks and ticket booths, and lines of cars form at freeway exits. Waiting lines occur, in fact, whenever and wherever the number of demands on a resource in some time span exceed the capacity of that resource. A cashier serves only one customer at a time, and the number of lanes in an exit ramp limits the number of cars that can pass a given point at the same time. The pattern of entrance to and exit from a waiting line is that entities (such as people or cars) are served in the order in which they arrive. A waiting line with this pattern of entry and exit from it is said to be a queue, a FIFO list. FIFO, (First-In-First-Out) is in contrast to a LIFO, (Last-In-First-Out) list, a stack.
The effect of a waiting line at a resource is to smooth out an arrival sequence, the times of arrival of entities. Items remain in the queue until the server (the resource) can process them. Items arrive at the rear and leave at the front, rather than arriving and leaving at the top as they do in a stack.
Suppose that jobs tagged by letters W-A-I-T-S arrive at a milling machine from other stations in a machine shop at irregular intervals, but the milling process takes three minutes for each job. If the times of arrival from start-up are 5, 6, 8, 9, and 13, then a queue would form. Figure 5.1 shows snapshots of the queue contents at arrivals and departures.
Arrival times of 5, 8, 11, 12, and 14 produce output at the same times, but the arrival sequence 5, 8, 12, 13, and 14 does not do so because the server is idle part of the time.
Now suppose that the service times are 2, 1, 5, 5, and 2. Figure 5.2 shows the new snapshots. The distribution of arrival times and the distribution of service times both affect the queue length and the amount of time that an entity spends in a queue. This is queueing behavior, a basic model from which the idea of a queue is derived. Such behavior is central to simulations and other applications, and is treated in more detail in section 5.1. Waiting lines will occur, and some feel for where and when they do is an aid in the design of programs.
A queue can be stored and managed as a data structure QUEUE. Like ARRAY and STACK, QUEUE is not concerned with the complexities of the flow of a sequence of items through it, but only with access to cells. Queueing behavior is to be distinguished from the data structure QUEUE, which is simpler to deal with than the behavior it models.
In a program, items seldom wait for a specific time to arrive, but they do wait for some process to complete (as do drivers at a traffic-light controlled by pedestrians). An input routine waits for a user to hit one or more keys, perhaps saving a string of keyed characters until they form a recognized token before allowing some other process to be initiated. On the other hand, processing of one input token may take longer than the entry of the next one. Systems that queue inputs and those that sometimes treat the keyboard as a nonentity have differing psychological impacts on the user.
Examples of queueing abound in the operating systems and in the hardware of computing systems. For instance, in a time-sharing system some jobs wait for service from a disk drive or a printer while another job is being processed by the CPU (Central Processing System). The common use, however, is simply to store items, in order, for later processing.
Queueing is fundamental to some of the applications of stacks in Chapter 4. The conversion of an infix expression to a postfix expression in section 4.2.2, for example, creates a queue called PostX--the postfix expression itself. The token stream PostX is a queue because tokens are both inserted to it and removed from it in the order in which they are encountered during execution of a program or during translation in a compiler.
From the viewpoint of processing tokens, stacks and queues are used in conjunction in a stack machine only to save a token and temporarily delay the processing of operands encountered in sequence in the token stream. In FORTH, the programmer creates the token queue. In Pascal, a compiler that translates to p-code creates the queue. In both these languages, the preparation of a queue is crucial to the successful operation of a stack. The stack eliminates the necessity to look ahead an arbitrary (and varying) number of predetermined tokens to decide when to insert the current token into the processing queue. Use of a stack allows the rest of the processing applied to the token stream to be done sequentially.
Queueing behavior is common in machine shops (and other manufacturing facilities), where jobs tend to back up somewhere: at a lathe, at a milling machine, at any work station where job requests arrive at a rate faster than the throughput determined by the mean service time of the work station for such jobs. Queueing behavior also occurs in the flow of goods from manufacturers to customers.
Machine shops, marketing systems, and computing systems are examples of networks where jobs (or other entities) flow from one server to another and where jobs may spend more time waiting than being served. Service is distributed in such systems, as it is in service networks of all kinds. Where service occurs in a network through which requests for service flow, so does queueing behavior. Analysis of queueing networks, done both analytically and operationally, is based on the behavior of an isolated queue, and that behavior is the pattern for the data structure QUEUE.
A data structure that models queueing behavior must do so through general data structure operations tailored to that behavior:
Queues need to be created with access (by pointer or index) to both a head (front) and a tail (rear), because insertions take place at the rear and deletions at the front. The formal operation which gives birth to a queue is CREATE.
A queue becomes empty at any time when there have been as many departures as arrivals. The formal (Boolean) operation that checks the viability of a queue is EMPTY.
A queue grows iff a single item is inserted into its rear position. No way of assigning values directly to queue items is available in a pure queue. The formal operation that inserts a value into a queue is INSERT.
The only retrievable value of a queue is the value of its front item. The formal operation that returns the value of the front item is FRONT.
The front item must be removed from a queue if the values of the other items are to be retrieved. The formal operation that removes the front item from a queue is DELETE.
The behavior of a queue (as a data structure) is entirely described, however it may be implemented, by CREATE, EMPTY, INSERT, DELETE, and FRONT.
A queue changes size with insertions and deletions and so is dynamic. It is created without knowledge of its future size and so is blind. It is sparse because the collection of potential entries is generally much larger than its actual entries at any given time. All of these thkngs make the pointer-linked list of records a natural support structure for the queue.
A queue provides direct access, although only at the front and rear, and that access should be efficient. Hence, if the maximum size of a queue is predictable, an array is a natural structure for queue support.
A formal structure QUEUE defines a data management policy, independent of implementation. Implementation, however, affects program writing. To contrast the two natural implementations, suppose that two queues are to be managed by a program: Q1, implemented with a linked list, LinearQ, and Q2, implemented with an array, aQueue. Figure 5.3 depicts the two queues.
The scheme depicted in Figure 5.3 for the implementation of a queue in an array has a peculiarity: the index Front is one less than the actual index of the front value. The neatness of this scheme becomes apparent when queue operations are developed as procedures.
As two items are deleted from LinearQ and a node of value 2 is inserted, snapshots of Q1 would look like those in Figures 5.4 and 5.5. (The terms Head and Tail have been replaced by Front and Rear as a reminder of the waiting-line model of queueing behavior.) A queue is a list structure for which insertion is always done with InsertTail and deletion with DeleteHead. In contrast, when the list of Figure 5.3 is treated as a stack, insertions are made with InsertHead. For this example, the difference would be the placement of the value-2 node at the front of the list, rather than at the rear. This difference is significant; queueing behavior is quite distinct from stack behavior.
Exercise E5.1 is appropriate at this point.
When this same set of operations is applied to Q2, a quirk of the array implementation of a queue becomes apparent: deletions and insertions move a queue along in its substrate array: they have an inchworm effect. The effect on Q2 of DELETE, DELETE, INSERT 2 is shown in Figure 5.6. No new insertions can be made to Q2 (in this implementation, with the value of Max as shown) without shifting the entire queue Q2 within the substrate array aQueue. The array index Rear has reached its limit Max, but the array aQueue is not filled by Q2. It is convenient to develop a procedure, ShiftQ, to deal with the shift.
5.2.1 Queue Management Algorithms
A comparison between the management routines for Q1 and Q2 can now be made. (An assumption is made that with LinearQ do . . . is in effect where it is convenient for Q1. The identifiers InsertRear and DeleteFront replace InsertTail and DeleteHead to emphasize the specific application to queues.) For comparison, the list form of InsertRear in Table 5.1 accepts values instead of nodes.
Values rather than nodes are inserted into LinearQ to emphasize similarities with routines applied to aQueue. Sentinel lists, convenient for some applications, require little change in the procedures.
Exercises E5.2 and E5.3, problem P5.1, and programs PG5.1 and PG5.2 are appropriate at this point.
A sequence of I (insert) and D (delete) commands that manage an input file as a queue are processed in essentially the same way as they were for a stack at the end of section 4.1.1.
Note: A realization in Pascal of the command loop as a "queue machine" is to be found in Part II, section I.
A queue can be displayed as a list by a simple variation of LT in section 3.3.2; but, as a queue, there is no access to internal nodes. One way to list a queue is to display the front node, delete it, and insert it back into the queue:
Queues are sometimes chosen to model a pervasive natural system, the waiting line. In many systems waiting lines are unavoidable. The effects of waiting on a time sequence of entities passed through a queue can be complex, but the data structure QUEUE is relatively simple. It does, however, take more care than does STACK. In pointer-linked record form, access to the tail node (the rear node) must be provided to make INSERT an O(1) operation. When supported by an array, not only is the maximum number of entries limited, but the inchworm effect can also occasionally force an O(n) shift operation of the queue within its array. (This problem can be alleviated with the use of circular lists as a support structure, as described in section 5.3.) The queue is more complex to manage, as a data structure, than is the stack.
The queue is a dynamic, immediate structure, and it can make efficient use of time and space. Above all, a queue is a retainer--it retains the order in which items enter it and produces them as needed.
Note that the word "queue" is commonly used to refer to structures more general than QUEUE. Generalizations of QUEUE are outlined in section 5.4, introduced in section 8.5.2, and applied in Chapter 10. One use of QUEUE is to provide a basis for its own generalizations.
Nodes linked into a cycle, like the list in Figure 5.7, were introduced in section 3.7:
A circular list may be maintained as a queue by the proper choice of INSERT and DELETE operations: InsertAfter and DeleteBack, both discussed in section 3.7. The result is a queue supported by a circular list, but it is commonly called a circular queue. A queue is said to be a linear structure, but it is actually a point structure, because only two points of a queue exist for the outside world, whatever its implementation. (If the queue is a two-point structure, then the stack is a one-point structure.)
In a queue maintained in an array, circularity can be transferred to index-management in the substrate array. An awkwardness inherent in the implementation of a queue with an array is that the queue array may not be full even though the cell of maximum index is in use--hence, the procedure ShiftQ in section 5.2. This inefficiency can be resolved in an array dimensioned a[0 . . Max - 1] with the help of modular arithmetic. In that case
calculates a remainder upon division by Max, and so has the same effect as:
The effect is to bend the array itself into a (virtual) ring, shown in Figure 5.8.
The assignment (1) is a clockwise index shift, no matter what the value of k, 0
Now Front and Rear can both be moved clockwise when a deletion or addition is made, as shown in Figure 5.9.
If no more than Max - 1 items are allowed into the queue, then (Front = Rear) signals that the queue is empty; and, after (Rear
The queue operations become:
Problem P5.2 is appropriate at this point.
Queueing behavior is exhibited in structures that are not queues in the strict sense. One of these is called DEQUE (double-ended-queue). This structure allows both entry and exit at either end, but nowhere else. Why it is not called a double stack is a mystery, since that is at least as accurate a description. If two nodes are inserted at one end and removed from the other, they will exit in queue order. If they are both removed from the entry end, then they exit in stack order. If they are removed from opposite ends, then their exit order is whimsical.
A queueing generalization of much greater utility than the deque is the priority queue. A priority queue is a structure in which nodes have a priority. This may be the key or other value, and it may even be possible to update the priority of a node. Retrieval from a priority queue is of the node with highest priority and no other. In that sense, there is one "front" node. At retrieval time, the entry order per se is of no significance.
Note: It is not uncommon for the term "queue" to refer to a structure that proves to be a priority queue on close examination. This meaning may even be more common in the general literature than that of pure queue.
A priority queue may be supported in many ways. One such is simply a sorted list, and the highest priority item in the queue is the head node. Another priority queue is an instance of QUEUE in which priority is the negative of the entry order (or the inverse of it). Another priority queue is an instance of STACK in which priority is given to the most-recently entered item (the entry order itself is the priority measure). There are many other ways to support priority queues.
One application of priority queues is as a retainer for events that have been scheduled to happen. Discrete-event simulations are those that move from action to action, and in such a simulation, this holding structure is called an event queue. An example of an event-queue application is the doctors'-waiting-room model treated in section 5.7.
Note: A Pascal program that simulates an airport customs process is to be found in Part II, section K. The heart of the simulation is the management of an event queue.
A common way to support a priority queue so that insertion and retrieval are efficient when entry order does not determine the priority is a heap, discussed in Chapter 8. A major application of priority queues is made in the treatment of graphs in Chapter 10.
In some sense, this book is a bridge between the array of introductory programming and variations of priority queues used in practice.
A buffer containing data to be written on a printer or a disk is usually generated at a different rate than it is serviced. As a consequence, either these jobs are retained in a queue, or some process must become idle until another is complete. Such queues may be managed by either software or hardware, since both can perform the same essential logical operations.
Some queueing within computing systems is normally the domain of hardware, rather than software. Instructions in a machine are fetched, then executed, in an endless cycle. Both the execution phase and the fetch phase can exhibit overlap in which two or more instructions are being processed in some way at the same time. Specifically, these two overlap modes are pipelining and the use of cache memory. They are both associated with queueing behavior.
Note: Discussions of pipelining and cache memories are to be found in Part II, section J.
Many physical processes are expensive or impractical to observe directly, and certainly they can only be observed in operation during conditions that actually exist. Almost any industrial process, almost any natural biological, physical, or social environment, and almost any large computing system is quite complex. For example, building a large chemical plant based on a newly discovered sequence of reactions without knowing that it will work on a large scale much as it does in the laboratory would not be wise. In such a case it is worthwhile to model such processes and to study the model extensively, with the assumption that the behavior of the model is a valid surrogate for the behavior of the process itself.
If suitable approximations to a process behavior can be constructed mathematically, it is often cost-effective to use mathematical software to study that behavior. An alternative, sometimes the only one, is the development of a simulation of the process. A simulation is a program that imitates the behavior of a process, in contrast to an analytical model, which describes it.
When simulating a system involving queues it is not necessary to use queues as a data structure in the simulation program. It is natural, however, and may be efficient in several ways. Queueing behavior may also be effected with structures that are not strictly of type QUEUE, such as a generalized (priority) queue. On the other hand, queues are often involved in simulations that do not themselves emulate queues, as a scheduling structure, the event queue. In practice, the "event queue" is usually a priority queue.
The conjunction of these ideas can be illustrated with a model of a doctors' office that does not explicitly involve a queue, but does use queueing ideas, and that is programmed with an event queue. Some familiarity with statistical ideas is helpful (see Part II, section A).
The office is serviced by five doctors and several support staff. Patients arrive in some distribution during an eight-hour day, are treated after a while, and leave. The treatment-with-wait generates a mean-service-time, mst, as a whole, shown schematically in Figure 5.10.
At random intervals one of the doctors is called away and returns after a random length of time. The number of services can vary from 0 to 5. One question that can be asked is: how many chairs are needed in the waiting room?
Four distributions are involved in this model:
ia, the interarrival time, or time between patient arrivals. (This would generally be modeled as an exponential distribution: ia
fixup, the mean service time for one doctor to treat one patient (possibly exponential again)
out, the time between doctor exits (possibly uniform, Rand)
back, the length of time a doctor will be gone when called away (perhaps a normal distribution)
These distributions can be generated either as needed or as four sequential files, to be stored and retrieved as needed. They are, in effect, queues. At any given moment, the next event might be a patient arrival, a patient exit, a doctor exit, or a doctor arrival. Each event can be described by a procedure that is simple or elaborate, depending upon how much detail is defined by the model and how much information is to be gathered for statistical analysis.
The event procedures need to be scheduled. One reasonable approach is to take care of the next (in time) event next.
Simulation programs often deal with event scheduling by having each event-procedure determine when the next event of its type is to occur, by generating it or reading it from a file and then generating a record to be added to the event queue. This record is called an event. The event-record contains the time at which it is to take place and other attributes of interest. Above all, it can produce the next event--the one scheduled to happen soonest--considered to be the event with the highest priority. In terms of the structures studied so far, the event queue can be maintained as an ordered list. Event-procedures process event-records, selected for processing by their position on the event list and their attributes.
It is necessary to resolve collisions, times occupied by more than one event, as well as other aspects of the program that affect the validity of the model. (The validity of a model is how well its behavior conforms to that of the system being modeled.) For example, is it valid to allow a doctor to leave while treating a patient, or must the service be completed? (Are there any emergencies?) Should patient arrivals be handled before doctor arrivals in collision with them? (This affects the number waiting and hence the statistics generated by the program.) Since collisions can occur, the priority used to sort events to determine their order of processing cannot be simply their scheduled event time.
Suppose that in a program Infuse, which simulates the doctors' office, the event list is named eList and contains records of the form:
Types of events would reasonably include but not necessarily be confined to, SadSack (a patient arrival), CoolOff (a patient moves to an examination room), Aok (a patient departure), StatOut (a doctor departure now), AgainSam (a doctor arrival). The time might represent minutes from the start of the day. An integer Avail might be used to keep track of the number of doctors currently available, and Waiter the number being served.
Suppose that the current event list is of the form shown in Figure 5.11. When the next record of eList is retrieved, it is found to be at (simulation) time 106. When it is removed for examination the result is the list of Figure 5.12:
When the retrieved record is examined, it is found to be a patient arrival (SadSack). As part of the execution of the procedure that handles patient arrivals, at least one new record will be scheduled:
The next SadSack record is scheduled at the time determined by the next ia value.
If patient arrivals have precedence over patient departures, but not doctor departures, then various values of ia that produce collisions would instead yield the snapshots shown in Figure 5.13.
The patient who arrived at time 106 does not disappear -- even though the arrival event disappears. The arrival procedure increments a counter representing the "queue" of patients in the waiting room. If individual patients are to be tracked through the process, then the waiting room may become a true queue structure, and a record is added to the rear of that queue when SadSack events are processed. Patient attributes such as illness type might be chosen at that point, if they are to affect the simulation. If so, service times must be split into categories.
A simulation program having a reasonable degree of validity involves many decisions, some hidden deep in the coding. Writing a simulation program is time-consuming and hence expensive; worse, it is very difficult to establish validity. Nevertheless, simulations are sometimes the most cost-effective approach to exploring a problem, but mathematical analysis should be tried first. For this reason, a great deal of effort is expended on approximate solutions to problems that are unsolved (or intractable). An alternate approach, available at major installations, is the use of simulation languages--languages written especially for this purpose. A discussion of the pros and cons of their use lies outside the bounds of this book.
Project PJ5.1 is appropriate at this point.
Note: A realization in Pascal of a simulation of the customs system at an airport is to be found in Part II, section K. It is based on the use of a priority queue.
Simulation begins to be accessible with a knowledge of queues, but the crux of a simulation is the thoughtful analysis of the results. That requires a background in statistics. The simulation language SIMULA is perhaps the easiest for the user of languages related to pseudocode to learn. There are introductory texts for SIMULA, but compilers are not common.
Queueing behavior is that of a FIFO (First-In-First-Out) collection. It is to be found wherever there are waiting lines, and waiting lines occur wherever an arrival sequence and a servicing process are not synchronized, a common pattern. The time-sequencing effects of queueing can be complex, but the data structure used to model it is relatively simple. A queue has the effect of storing items until they are needed. It is a retainer.
Formally, QUEUE is a structure in which only the oldest (earliest-entry) item in the collection is accessible for viewing by FRONT or for removal by DELETE. An interior node can be accessed only by deleting the items in front of it. Like lists and stacks and unlike arrays, queues are dynamic, growing with insertions and shrinking with deletions, but they are point-like objects that hide their internal dynamism from the user.
Queues can be supported as lists to which insertion is applied at the rear (tail) and deletion at the front (head). A queue can also be supported in a direct way in a single array, using two indices Front and Rear.
The array-supported queue can reach the last cell in its array in two senses--by position and by total number of entries. The shifting required to resolve the position problem causes insertion to be O(n) in the worst case, although it is typically an O(1) operation like deletion.
The position problem for an array-supported queue can be eliminated by using circular queues, but then an extra flag is required to resolve empty and full conditions.
The queue has generalizations, one of which is the priority queue, to be explored in later chapters. Many applications of programmed queues involve the generalized forms, but pure queues have uses such as the pipelining of instructions and simulations of waiting lines.
A realization in Pascal of a "queue machine" is to be found in Part II, section I, and a Pascal program that simulates an airport customs system is to be found in Part II, section K.
Exercises immediate applications of the text material
E5.1 What would the final list be if the sequence: 4 0 - 5 10 were treated as a stack with operations DELETE, DELETE, INSERT 2?
E5.2 Trace the behavior of the queue: 4 0 - 5 10, implemented with pointer variables, with the operations: DELETE, INSERT 2, DELETE, DELETE, INSERT 3, DELETE.
E5.3. Trace the behavior of the queue: 4 0 - 5 10, implemented as an array, with the operations: DELETE, INSERT 2, DELETE, DELETE, INSERT 3, DELETE. Assume that the value 10 is initially in aQueue [Max - 1].
Problems not immediate, but requiring no major extensions of the text material
P5.1 Redesign the procedures for an array implementation of queues in section 5.2, using Front as the index of the front value itself.
P5.2 Modify the queue operations of section 5.3 so that up to (Max - 1) items may be kept in a circular queue implemented as an array, and Some is not required.
Programs for trying it yourself
PG5.1 At the beginning of this chapter, an input stream of characters was associated with both an entry time into a waiting line and a service time. Together these times determined the contents of a queue.
Write a program that accepts a sequence of triplets--for example, (W,5,2), (A,6, 1), (I,8,5), (T,9,5), and (S,13,2) --and produces a snapshot of the queue each time there is a change in it. The triples are to be (identifier, arrival time, service time) and the time at which a change in the queue occurs should be displayed with its contents.
It is not a bad idea to produce two versions of this program, one using pointer-linked records, and the other using array support for the queue. Obviously, only a few procedures should change from one version to the other.
PG5.2 A buffer B holds N blocks of data to be displayed by output device P. Programs generate blocks of output at random intervals with a mean of 11 seconds, and they are queued in B. P removes a block from B at regular intervals, every 10 seconds when there is one to remove.
Suppose that, because of overhead and storage limitations, each increment of N above 1 costs an average of $1 for each storage of a block into B. Each time a program finds the buffer full, it must be rerun, at a cost of $100. Clearly, if there is no variation in the production of blocks, N = 1 is optimal. If there is variation, blocks are sometimes generated close together, and N = 1 will exact a cost of $100.
The problem here is to write a program that experimentally determines the optimum value of N for clearly stated conditions of spread (dispersion) in the generation of blocks. A simple variation is to use a pseudorandom number generator to generate times between blocks that vary uniformly in the interval [i . . j] (for example, in [7 . . 15]). The material in Part II, section A, will allow a much more sophisticated experiment to be designed with little additional programming.
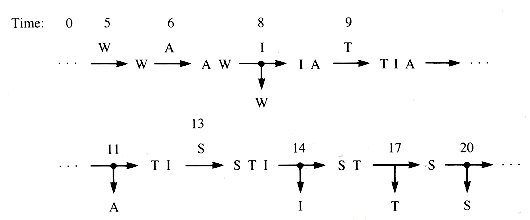
Figure 5.1
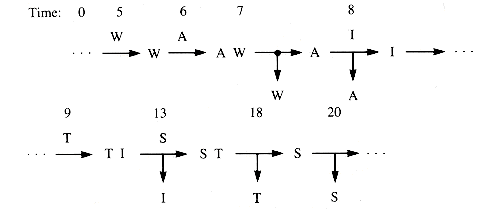
Figure 5.2
5.1 Queueing Behavior
5.1.1 The Queue Structure
5.2 Queue Implementation and Management
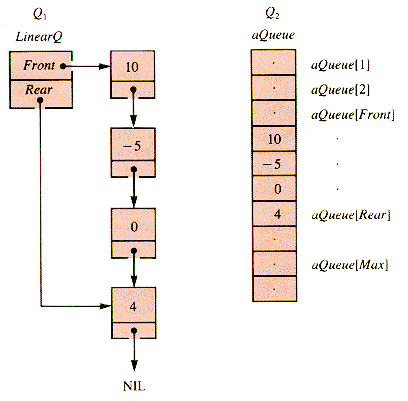
Figure 5.3
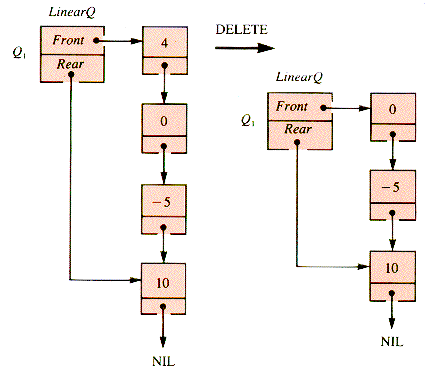
Figure 5.4
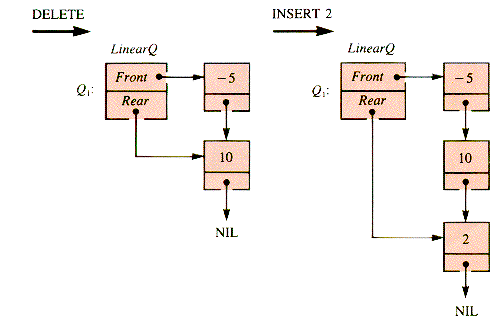
Figure 5.5
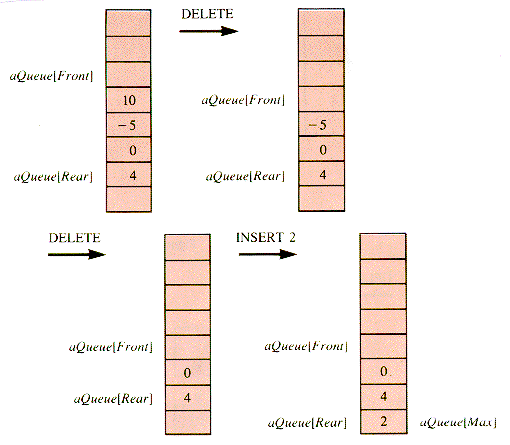
Figure 5.6
5.2.1 Queue Management Algorithms
Table 5.1
Q1 Q2
----------------------------------------------------------------------------------------------
CREATE
declarations {O(l) declarations {O(l)LinearQ.Front
NIL Front0 Rear
0----------------------------------------------------------------------------------------------
EMPTY
function Empty(LinearQ) {O(l) function Empty(aQueue) {O(l) if Front = NIL if Rear = 0
then return TRUE then return TRUE
else return FALSE else return FALSE
endif endif
end {Empty end {Empty----------------------------------------------------------------------------------------------
INSERT
procedure InsertRear(aQueue, i) {O(O(ShiftQ)) if Rear = Max
then ShiftQ(aQueue)
endif
if Rear = Max {stillprocedure InsertRear(LinearQ,i) {O(l) then {deal with a full-array error NEW(iNode) else Rear
Rear + 1 iNode
.Value i aQueue[Rearl i iNode
.Link NIL endif if Empty(LinearQ) end {InsertRear then Front
iNode else Rear
.Link iNode endif procedure ShiftQ(aQueue) {O(Max) Rear
iNode if Front > 0 end {InsertRear then for k = 1 to Rear-Front do aQueue[k]
aQueue[Front + k] next k
Rear
Rear - Front Front
0 endif
end {ShiftQ-----------------------------------------------------------------------------------------
DELETE
procedure DeleteFront(LinearQ) {O(l) procedure DeleteFront(aQueue) {O(l) if Empty(LinearQ) if Empty(aQueue)
then {deal with this error then {deal with this error else p
Front else Front Front + 1 Front
Front .Link if Front = Rear endif then Front
0 DISPOSE(p) Rear
0 end {DeleteFront endif endif
end {DeleteFront-----------------------------------------------------------------------------------------
FRONT
function FrontView(LinearQ) {O(l) function FrontView(aQueue) {O(l) if Empty(LinearQ) if Empty(aQueue)
then {deal with this error then {deal with this error else return Front
. Value else return aQueue[Front + 1] endif endif
end {FrontView end {FrontViewprocedure ListQ(q) {O(n) if Empty(q) then return endif
Start
q repeat
DISPLAY(Front(q))
Node
q Delete(q) {Delete should not include DISPOSE Insert(Node)
until Node = Start
end {ListQ5.2.2 On the Use of Queues
5.3 Circular-Track Queues
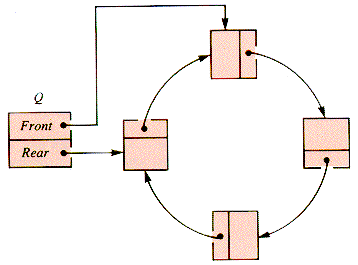
Figure 5.7
(1) k
(k + 1) MOD Maxif k = Max 1
then k
0else k
k + 1endif
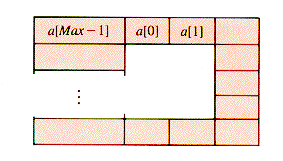
Figure 5.8
k Max - 1. This scheme forms a circular array without regard to the structure it supports, but it is normally used in support of a queue.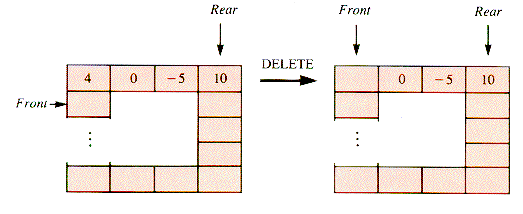
Figure 5.9
(Rear + 1) MOD Max), (Front = Rear) also signals that the array is full. If Max items are allowed into the queue, an additional flag needs to be carried in order to distinguish between the empty and full conditions. One approach (of several) is to use the flag Some, reset TRUE during insertion, and set FALSE when deletion produces an empty queue.function Empty {O(1)if (NOT Some) AND (Front = Rear)
then return TRUE
else return FALSE
endif
end {Emptyprocedure InsertCQ(x) {O(1)if (Front = Rear) AND Some
then {report full arrayelse Rear
(Rear + 1) MOD Maxa[Rear]
xSome
TRUEendif
end {InsertCQprocedure DeleteCQ {O(1)if Empty
then {deal with this errorelse Front
(Front + 1) MOD Maxif Front = Rear
then Some
FALSEendif
endif
end {DeleteCQ5.4 Generalized Queues
5.5 Queues in Hardware (optional)
5.6 On the Simulation of a Doctors' Waiting Room (optional)
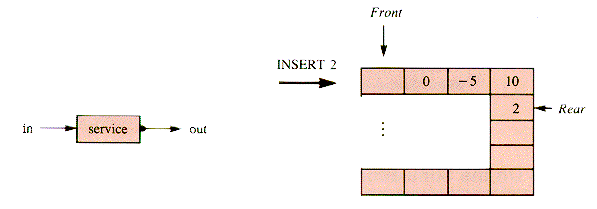
Figure 5.10
- (1/
) 
1n (Rand).eListype = RECORD
Time : INTEGER
Tag : INTEGER {patient IDType : ARRAY[1 .. 8] OF CHAR
Info : {a record of attribute informationLink :
ListypeEND {eListype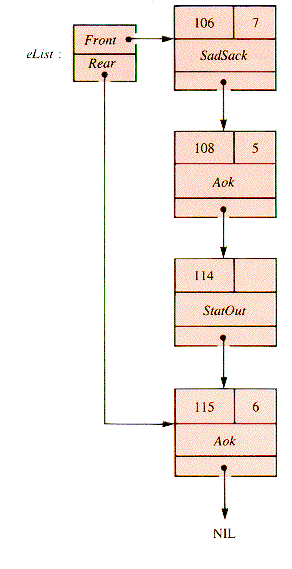
Figure 5.11
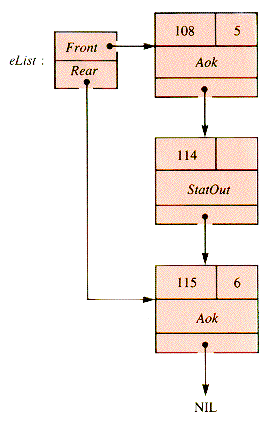
Figure 5.12
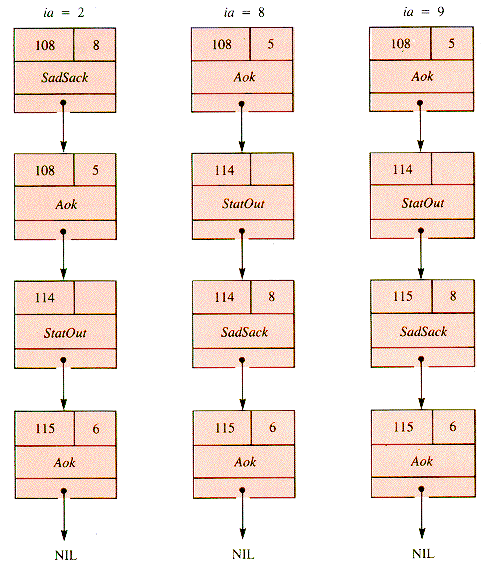
Figure 5.13
Summary
Exercises
Problems
Programs