Stacks can be implemented in arrays without the use of link indices, but linked lists are also a natural way to discuss stacks. Consider the linked list in Figure 4.1.

Figure 4.1.
If two deletions are made from the top (the head) of this list, and the value 2 is added at the top, the effect is to carry out the operations:
DELETE
DELETE
INSERT 2
The resulting snapshots of the list are shown in Figure 4.2.
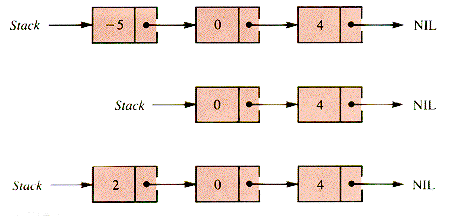
Figure 4.2
In terms of the list-processing routines of Chapter 3, a linked-list structure is a stack iff insertion is restricted to InsertHead and deletion is restricted to DeleteHead.
4.1 The Stack Structure
Stacks need to be created, like any other structure, but insertion and deletion both occur at the top (the head), so no tail pointer or index is required. The formal operation that gives birth to a stack is CREATE.
Activation of a stack is usually accompanied by initializing the top pointer to NIL (or u). A stack may grow and then decrease until it is again empty, as though freshly activated. The formal (Boolean) operation that checks the viability of a stack is EMPTY.
A stack grows iff a single node is inserted into its top position. No way of assigning values directly to stack nodes is available in a pure stack. The formal operation that inserts a node into a stack is PUSH.
The only value of a stack accessible to its environment is the value of its top node.
The only retrievable value of a stack is that of its top node. The formal operation that returns the value of the top node is TOP.
The top node must be removed from a stack before the values of other nodes can be retrieved. The formal operation that removes the top node from a stack is DELETE.
The behavior of a stack is entirely described, however it may be implemented, by CREATE, EMPTY, INSERT, DELETE, and TOP, and their interactions. TOP followed by DELETE, implemented as one operation, is called POP.
However a stack is stored, it can be used to alter a sequence of values. For example, the input stream of characters S-T-A-C-K can be arranged in reverse order by stacking them and then unstacking them, as depicted in Figure 4.3.
The output produced by the pops is: K-C-A-T-S.
Figure 4.4 shows that the consonants can be moved after the vowel A by stacking them as encountered. The output produced by the pops is: A-K-C-T-S.
This process is easily generalized into the separation of two classes of items in a stream into leading and trailing segments in O(n) time.
Railroad cars are separated on siding tracks in just this way, although more than one siding (stack) may be needed for more than one category of car.
With the aid of more than one stack, shuffling can become more sophisticated. Suppose the letters l-N-P-U-T-S-T-R-E-A-M are placed in stack S1 in nondecreasing order, and the others shunted to stack S2 as in Figure 4.5.
Unstacking of S1 followed by unstacking of S2 forms a new stream: U-P-N-I-M-A- E-R-T-S-T. Now this stream may be reversed (by stacking it, for example) to form: T-S-T-R-E-A-M-I-N-P-U. Apply the process in Figure 4.5 to the new stream, depicted in Figure 4.6.
If S1 and S2 are unloaded with the help of a third stack as before, the resulting stream is: S-R-E-A-M-I-N-P-T-T-U.
Surprising as it may seem, six more repetitions of this process will produce the sorted stream: A-E-I-M-N-P-R-S-T-T-U. Try it!
Devising a sorting routine from this process is project PJ4.1.
Project PJ4.1 is appropriate at this point.
Two natural implementations are a list structure, which uses pointer variables, and an array-management scheme. If the list is called liStack and the array is called aStack, then the same data set takes two schematic forms, shown in Figure 4.7.
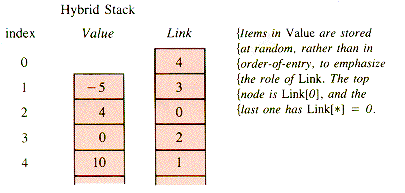
There is also a hybrid form, in which a stack is implemented as a linked-list structure, which in turn is supported in arrays:
This form is seldom used and will not be pursued.
Any stack supported in an array must be programmed with some concern for the maximum possible index, Max. A variable, Top, is required to locate the top item in aStack. Table 4.1 allows comparison between the two major treatments by examining the stack operations in parallel. For comparison, the linked-list form of Push accepts values instead of nodes. Note that all of the stack management routines are fast: O(l). This intrinsic efficiency promotes the use of stacks in applications.
The programming that manages a stack with an input file (such as a sequence of keyboard entries) is straightforward. For example, a sequence of commands of the form: I (for INSERT), and D (for DELETE) can be processed by this loop:
Commands to invoke TOP or the display of the complete stack are easily added to the preceding command loop. Difficulties (challenges) arise from exception handling (dealing with errors) and from the quirks of individual applications.
A command loop like the one above is thought of as a shell that surrounds the machinery of resource management. It forms an interface with the user, who sees it as a virtual machine. The user supplies commands that evoke a response. From the user's view, the loop is a machine that does whatever the commands say to do.
The details of how the response gets done internally are of no concern at the command level. This kind of deliberate information-hiding is also present in the use of a data structure, and the concept of a virtual machine is a major guiding philosophy in the design of a modern operating system.
The shell format that professionals use to deal with complexity is well worth imitating.
Note: A realization in Pascal of the loop above as a "stack machine" is found in Part II, section E.
The display of a stack can be carried out by standard list procedures but only if the stack is treated as a list, not a stack. As an instance of STACK, display of the contents proceeds the same way as the display of the contents of a crowded closet or a full deep-freezer: items are popped off the stack, displayed, and then pushed onto an auxiliary stack. Restoration is a reverse of this process, without the display. It is more reasonable and common practice to forgo rigid formality and use a list-walk to display the contents of a stack.
Note: STACK is a structure that does not require a traverse in most applications. There is no direct access to interior nodes. For other data structures in the book, with the exeption of QUEUE, the traverse is a fundamental skeleton for constructing algorithms.
Stacks are sometimes chosen as a data structure simply because they model behavior that occurs in the system to be modeled (as would be the case in a cafeteria simulation). Actually, modeling natural stack behavior may not even require a stack, as indicated in section 4.5. Stacks may also be chosen to deliberately shape a computing scheme.
Stacks are dynamic--growing and shrinking at will--but that fact is hidden from the user who sees only the top item. Stacks are blind because it is not necessary to know their potential size when they are created. Stacks can be sparse because no interior item in a stack occupies a special place in it--only the sequence of PUSH and POP operations determines where in a stack an item is to be found. Furthermore, it does not matter except to determine when an item reaches the top. All of these features indicate that a linked list is a natural support for a stack.
Stacks provide O(l) direct access, although only to one item at a time, and the direct access moves from one item in the stack to another. That indicates the utility of an array as a natural support for a stack.
Neither support system captures the nature of the stack in and of itself, which arises from two major attributes:
1. A stack can resequence a stream of entries.
2. A stack is immediate. Entry and exit from a stack are O(l) operations. What you get is what you see on top; there is no apparent depth or size or structure to a stack. In some sense, a stack is a point-like structure.
Above all, a stack is so very easy to use, if what you want from it is the last thing put into it.
The game described below comes trom Nancy Griffith of Georgia Institute of Technology. It is introduced hereto serve as an example of the use of multiple stacks and as a source of assignments.
A deck of cards can be represented by 52 symbols, tour each of: A, 2, 3, . . . , 9, 10, J, Q, K. They may be regarded as the numbers 1 . . . 13. Suppose one card at a time is dealt from the deck and placed onto one of four foundations so that cards in the foundations F1. . . F4 are in the order:
This is not possible for most shufflings of the deck, of course, but it can be done with the help of four waste piles, W1 . . . W4. The top of any waste pile can be used as a source for a card to be moved to a foundation at any time.
One of the possible strategies for the use of the waste piles is to deal from the deck onto them in the order W1, the W2, W3, W4, W1, . . . but to move a card from a waste pile to a foundation whenever possible. A program can be written to accomplish these moves and verify the result.
A shuffle can always be produced from a real deck of cards; the order produced in the real world can be used as an input stream. The professional approach is to use a random number generator (see Part II, section A). With each of the 52 card symbols S[i] arranged in some standard order, associate a pseudorandom number RN[i], as shown in Figure 4.8. Now sort S, using the values in RN as a key. The symbols of S will be distributed as randomly after the sort as the values in RN were before the sort.
This is a valuable exercise to do with all three variations of stack support in order to compare them and develop a feel for their commonalities and differences.
Program PG4.1 is appropriate at this point.
Conversion of infix expressions to postfix form depends upon the precedence of operations. To know that multiplication is done before addition in the expression A + B * C requires a "look-ahead" process, because the addition may or may not be applied immediately to the operands A and B that bracket it. It is true, in contrast, that A + B - C is equivalent to (A + B) - C in most languages.
In order to process a postfix expression left-to-right in the manner indicated, the tokens in the expression must be sequenced so that the operations occur in the order in which they are to be performed. With a little practice, one can spot the appropriate order. For example, the equivalent infix and postfix forms of several expressions are:
A stack may be used to provide the same effect.
Parentheses complicate the conversion because they override the precedence and must be dealt with in some manner.
As a simple example, suppose that operators are restricted to:
A common assignment of precedence would be:
A further assumption is that operators on the same level of precedence are to be evaluated left-to-right.
By examining the four variations of the example expression we can see that:
When an operator is encountered, it is not put in the postfix list PostX until its operands have been acquired. It may be retained on a stack, OpStack, until its proper postfix position is reached. This position is determined by the processing of a sentinel value, a right paren, or an operator with precedence at least as low.
If an operator that has been retained is of precedence higher than or equal to an incoming one, then it is unstacked and added to the list. The sentinel value has the lowest possible effective precedence.
A left paren--"("--is placed on OpStack. A right paren--")"--causes the transfer of OpStack items to PostX down to a left paren. Both parens are discarded.
The behavior of the stack and the list for a * b + c & is depicted in Figures 4.13 - 4.15. The resulting list is quickly retrieved.
With a function Level that returns the level of an operator, the infix-to-postfix conversion becomes:
Exercise E4.2, problem P4.1, and program PG4.3 are appropriate at this point.
Conversion of infix expressions to postfix lists is not followed immediately by execution of the postfix list in most computing systems. The conversion normally occurs in a compiler, followed by translation of the list into instructions for a machine that may or may not provide stack operations directly. Nevertheless, the translation is driven by a process very similar to the execution of a postfix list. Schematically for A B C * + & in a postfix stack, the execution might proceed as in Figure 4.16.
Here "*" causes the generation of the machine instructions to multiply the values of the top two addresses on the stack, place the result in T1 and push the address T1 onto the stack. The translation algorithm then places T1 on its postfix stack, but the translated result of the encounter with "*" is simply the set of instructions equivalent to "multiply B and C and place the result in T1." The actual multiplication occurs at execution time, not compilation time, in a manner dependent on the machine architecture and details of translation. The postfix list and stack are used simply to organize the sequence of machine operations. A compiler is developed to translate a language into the instructions of a particular target machine. Several features of the design of the target machine might be used to make the resulting translation more efficient, but the essence of the stacking scheme is likely to remain in the design of the translation process.
Compilers are very complex programs, but much about them is general, if not universal; and the details of a specific target machine are only involved in parts of their design. Much of their generality and much of that machine isolation follow from the informed use of data structures.
Charles H. Moore invented a language, FORTH, which is now in use in many varied applications. It is difficult to determine how much of the power of available versions of FORTH is due to the central role of stacks in the design of the language, but stack ideas certainly give it much of its character. FORTH has a unique combination of properties, as it is commonly implemented and used.
Two aspects of FORTH are of particular interest in the context of this chapter:
1. Statement syntax is intrinsically postfix in form.
2. Statement semantics are based on stack manipulation.
These are independent properties, although they form a natural partnership. Partly because of this combination, the modularity of FORTH programs has a different flavor and genesis than that of, say, Pascal programs.
A very brief introduction to elementary FORTH is found in Part II, section F. It is included as an interesting example of stack management made explicit in a computer language.
When Pascal is translated into the intermediate code, p-code, the semantics of Pascal statements are translated into actions of a machine, the p-Machine. P-code statements are designed to invoke the possible actions of the p-Machine. For the translation of Pascal into p-code, it does not matter whether p-code will be executed directly in hardware. If p-code is further translated into machine instructions of a machine that is not a p-Machine, then the p-Machine that is the target of the translation is a virtual machine. The apparent operation of a virtual machine is the same as that of a hardware version, so an understanding of the p-Machine is still a guide for correct translation. To understand the p-Machine is to understand an elegant application of stack ideas.
A discussion of the p-Machine that is sufficient to program in p-code or to serve as the basis for a discussion of some of the aspects of HLL (High Level Language) translation is found in Part II, section G.
A stack may appear in a variety of guises--as a (physical or geometrical) model, as a formal data structure, as a programming technique, and in general as an idea. A program written to emulate the behavior of some process that apparently involves a stack may not actually use the data structure STACK.
Suppose a program models the conceptual behavior of the stock of canned flan on a grocery shelf. (Flan is custard in intimate contact with carmelized sugar.) A simple model is a stack of cans on the shelf. The public's desire for flan is sporadic, but it may be modeled either by a distribution derived algebraically from a uniform variate or by one derived from an experimentally measured PDF (Probability Distribution Function--see Part II, section A). In either case, a number of strategies for restocking the shelf are possible, each having costs associated with it.
If there is more than one stack of cans, the withdrawal, distribution, and restocking strategy between them determine such values as the mean number of cans on the shelf (in the stack or stacks). Pursuit of the many options is left to the exercises. Deeper questions of verification and the validity of a program model for the restocking problem are left to a course in simulations and models.
If the goal of the simulation is to determine the mean stack depth, the "stack" can be modeled simply with a counter. Each withdrawal decreases the count by one; restocking increases it by the number "added to the stack." Statistics may be gathered in several ways during the process to collect measurements of the stack depth.
Instead of mean depth, the desired information may be mean length of time that a can of flan spends on the shelf. (The carmel may crystallize after some length of time, causing rejection or dissatisfaction--flan has an estimated shelf life.) To determine mean shelf-time, a stack of can-records may be used, each marked with the (simulation) time at which they were stocked. Time passage statistics may be recorded when a can is withdrawn. A meaningful comparison study of "front-loading" and "rear-loading" restocking strategies may then be made from mean shelf-times. (Note that "rear-loading" defines a nonstack, a queue in fact--a structure studied in Chapter 5.)
Program PG4.5 is appropriate at this point.
Inexperienced cave explorers sometimes play out string as they trace out the twists, turns, branches, and interconnections of a cave. The string allows them to backtrack--to return to a previous branch point by gathering in the string and hence retracing their path backwards. The call . . . return model of subprogram invocation (as well as its more sophisticated variates), is an example of backtracking that uses a stack rather than string for a temporary memory.
Stacks can be used to backtrack during traverses of some of the structures yet to be introduced, in particular the binary tree of Chapter 8. Carefully structured traverses of data structures play a role in artificial intelligence, and some of them use backtracking. A very simple model of an "intelligent" behavior requires no background except ARRAY and STACK: this model of how to explore a maze with the aid of a backtracking stack is found in Part II, section H.
Stack behavior is that of a LIFO (Last-In-First-Out) collection. Formally STACK is a structure in which only the top, last-entered item is accessible. Like a list, it is dynamic, growing with insertions and shrinking with deletions. Unlike a list, interior items can only be reached by repeated removal of the top item. A stack does not require a traverse.
In all its forms, a stack is managed by CREATE, PUSH (insert), DELETE, and TOP (value return). All of these are O(1) operations, and so wherever a stack is appropriate it is highly efficient.
STACK may be chosen as a data structure because it models common behavior. When chosen as a deliberate design basis, it is used to resequence a stream of items or because it is an immediate structure that is very easy and efficient to use.
Stacks can be supported as lists restricted to insertion and deletion at the head only. The nodes can be linked records, linked with pointer variables or indices. A direct form of array support that is attractive and common because of its simplicity does not involve links, only an index Top. It does, however, have the universal limitation of array-supported structures: it can be asked to grow out of its array.
The stack structure has had a profound influence on computing; in the theory of computing; and in the design of language translators, processors, and computing languages. Processors and languages not only incorporate the concept of a stack as a tool, but some have also made it a central feature of their design.
Applications of stacks that are treated in the chapter include a stack-directed sorting scheme, the game Calculations, reverse Polish notation, the language FORTH, the p-Machine used by some versions of Pascal, and the use of stacks in simulations. Extended discussions of FORTH and the p-Machine are found in Part II, sections F and G.
Stacks appear in most of the later chapters. In section 7.2 stacks play a central role in describing variations of the programming solutions of a problem. In a number of places they are used to help rearrange a sequence of items.
A realization of a stack manager (in Pascal) is found in Part II, section E.
Exercises immediate applications of the text material
E4.1 Trace the growth and decay of the stack Post managed by function DoPostFix of section 4.2.1 for the following token streams:
E4.2 Trace the behavior of the stack OpStack and the list PostX as determined by procedure IntoPostFix of section 4.2.2 on the following:
Problems not immediate, but requiring no major extensions of the text
P4.1 The precedence of operations is not the same for all languages. Find three infix expressions (possibly including Boolean operators) that are legal in both of two languages but have distinct postfix forms. (BASIC and Pascal are worth examining in this context.)
Programs for trying it yourself
PG4.1 Write a program to play the game Calculation of section 4.1.3, using stacks implemented in one of the following ways:
(a) pointer-linked records,
(b) an array, or
(c) an array-based linked list.
This is intended to be used for up to three program assignments.
PG4.2 Write a program that uses the function DoPostFix of section 4.2.1 to evaluate a sequence of postfix expressions.
PG4.3 Encase procedure IntoPostFix of section 4.2.2 in a program that accepts infix expressions and displays their postfix equivalent. (Note that this program may be combined with PG4.1 to evaluate infix expressions.)
PG4.5 Write a program that simulates a flan-can row of a grocery shelf that holds 15 cans. Withdrawals are to be generated at random times with any of the distributions discussed in section 1.5. Restock at the front (top) when there are fewer than three cans on the shelf, and determine the mean-age-since-stocking of the cans on the shelf after 100 cans have been withdrawn. Run again with restocking at regular intervals.
Projects for fun; for serious students
PJ4.1 Write a program that uses two or more stacks to sort an input stream of up to 50 integers.
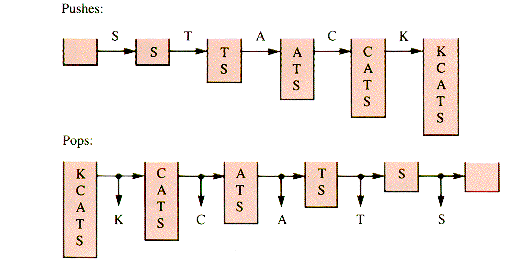
Figure 4.3
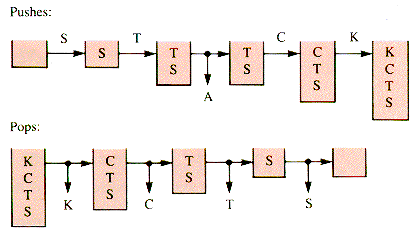
Figure 4.4
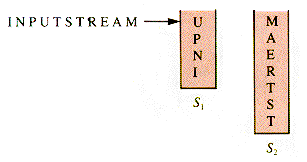
Figure 4.5
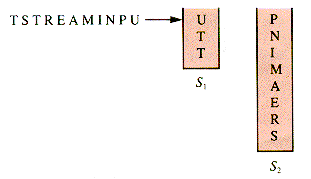
Figure 4.6
4.1.1 Stack Implementation and Management
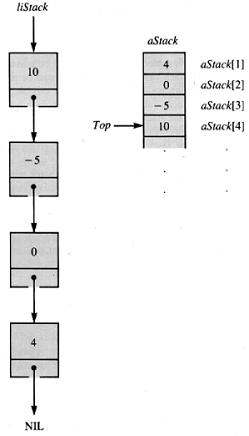
Figure 4.7
repeat
Read(Command)
case of Command
"I" : Read(Item)
Push (Stack,Item)
"D" : Delete(Stack)
"E": exit {E stands for End-Of-Fileelse: {deal with this errorendcase
forever
Table 4.1
liStack CREATE aStack
------------------------------------------------------------------------------
liStack
 NIL {O(l) Top
NIL {O(l) Top  0 {O(l)
0 {O(l)------------------------------------------------------------------------------
EMPTY
function Empty(liStack) {O(l) function Empty(aStack) {O(l) if liStack = NIL if Top = 0
then return TRUE then return TRUE
else return FALSE else return FALSE
endif endif
end {Empty end {Empty------------------------------------------------------------------------------
INSERT
procedure Push(liStack,i) {O(l) procedure Push(Stack,i) {O(l) New(iNode) if Top > Max
iNode
 .Value
.Value  i then {deal with this error
i then {deal with this error iNode
 .Link
.Link  liStack else Top
liStack else Top  Top + 1
Top + 1 liStack
 iNode aStack[Top]
iNode aStack[Top]  i
i end {Push endif end {Push------------------------------------------------------------------------------
DELETE
procedure Delete(liStack) {O(l) procedure Delete(aStack) {O(l) if Empty(liStack) if Empty(aStack)
then {deal with this error then {deal with this error else liStack
 liStack
liStack  .Link else Top
.Link else Top  Top - 1
Top - 1 endif endif
end {Delete end {Delete------------------------------------------------------------------------------
TOP
function TopValue(liStack) {O(l) function TopValue(aStack) {O(l) if Empty(liStack) if Empty(aStack)
then {deal with this error then {deal with this error else return liStack
 .Value else return aStack[top]
.Value else return aStack[top] endif endif
end {TopValue end {TopValue4.1.2 On the Use of Stacks
4.1.3 The Calculation Game (optional)
F1: A 2 3 4 ... F2: 2 4 6 8 ...
F3: 3 6 9 Q 2 5 8 ... F4: 4 8 Q 3 7 J ...
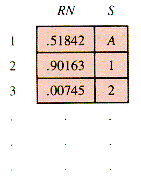
Figure 4.8
4.2.2 Conversion of Infix to Postfix
Infix Expression Postfix Expression
a * b + c a b * c +
a + b * c a b c * +
a * (b + c) a b c + *
(a + b) * c a b + c *
~, *, /, +, - {and parentheseslevel 3: ~
level 2: *, /
level 1: +, -
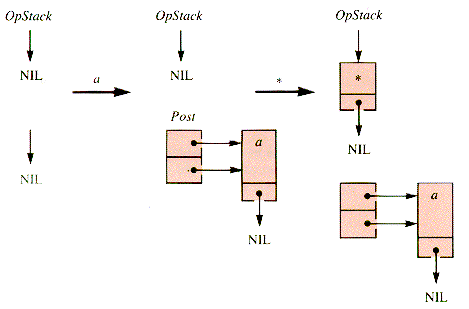
Figure 4.13
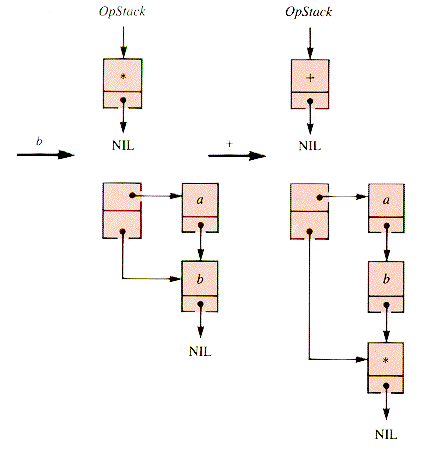
Figure 4.14
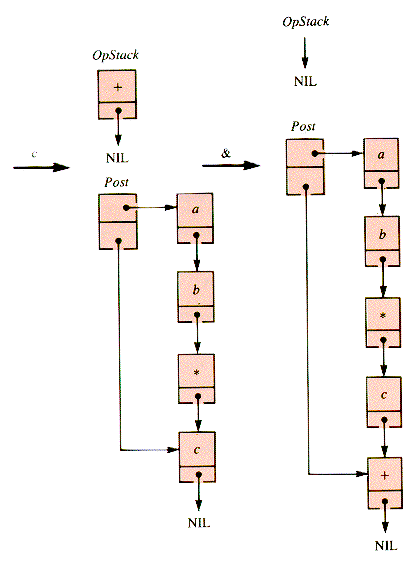
Figure 4.15
procedure IntoPostfix
Next(Token)
while Token
 "&" do
"&" docase of Token
{operand}: InsertTail(PostX,Token)")": begin
while NOT Empty(OpStack)
Op
 Top(OpStack)
Top(OpStack)Delete(OpStack)
if Op
 "("
"("then InsertTail(PostX,Op)
else exit
endif
endwhile
end
"(" : Push(OpStack,Token)else : begin {new operatorOp
 Top(OpStack)
Top(OpStack)while Level(Op)
 Level(Token) do
Level(Token) doDelete(OpStack)
InsertTail(PostX, Op)
if Empty(OpStack)
then exit
else Op
 Top(OpStack)
Top(OpStack)endif
endwhile
Push(OpStack, Token)
end
endcase
Next(Token)
endwhile
while NOT Empty(OpStack) do
Op
 Top(OpStack)
Top(OpStack)Delete(OpStack)
InsertTail(PostX, Op)
endwhile
end {IntoPostfix4.2.3 Postfix Lists in Translation (optional)
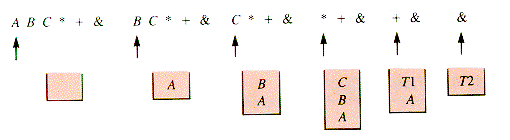
Figure 4.16
4.3 Stacks in the Language FORTH (optional)
4.4 The p-Machine (optional)
4.5 The Use of Stacks in Simulations (optional)
4.6 Backtracking with Stacks (optional)
Summary
Exercises
3 5 * 6 + &
3 5 6 * + &
3 5 6 + * &
3 5 + 6 * &
a * b + c & (a + b) * c &
a + b * c & 3 + ((a + b) * c) + d &
a * (b + c) & ~(a + b) * (c + d) &
Problems
Programs
Projects


