One way to measure impurity degree is using entropy. Entropy is the randomness collected by an application for use in decision that requires random data.
Entropy = Σ[-pj(log2pj)] for all jwhere
pj is the probability of the class value j.
For example, given that
Prob( Bus ) = 4 / 10 = 0.4 # 4B / 10 rows
Prob( Car ) = 3 / 10 = 0.3 # 3C / 10 rows
Prob( Train ) = 3 / 10 = 0.3 # 3T / 10 rows
we can now compute entropy as
Entropy = –0.4×log(0.4) – 0.3×log(0.3) – 0.3×log(0.3) = 1.571The logarithm is base 2. Entropy of a pure table (consist of single class) is zero because the probability is 1 and
log(1)=0.
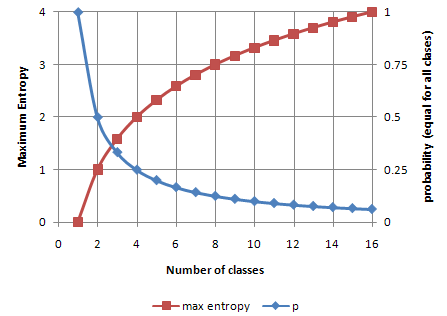
Entropy reaches maximum value when all classes in the table have equal probability.
The figure below plots the values of maximum entropy for different number of classes n, where probability is equal to p=1/n.
In this case, maximum entropy is equal to
-n*p*log pNotice that the value of entropy is larger than 1 if the number of classes is more than 2. |
|
|
Q: What did the elephant say to the naked man? A: “How do you breathe through something so small?” |