Pivot is first created with a sentinel value larger than either of the tail node values of a and b and then used as the tail node of both, as shown in Figure S.1.
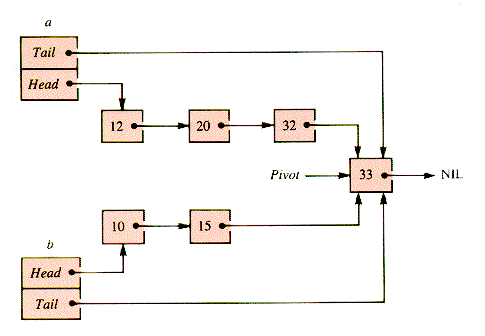
Figure S.1
The merging operation selectively removes nodes from a and b and adds them to the new list c, with head node Pivot  .Link, as Figure S.2 illustrates.
.Link, as Figure S.2 illustrates.
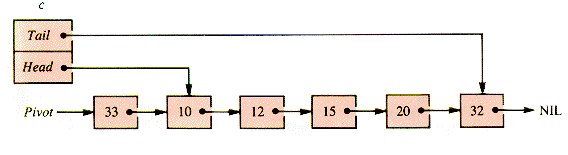
Figure S.2
Preparation for the merge is done by:
procedure Setup {O(1)
if a.Tail.Key
b.Tail
.Key
then Sentinela.Tail
.Key + 1
else Sentinelb.Tail
.Key + 1
endif
NEW(Pivot)
Pivot.Link
NIL
Pivot.Key
Sentinel
c.TailPivot
a.Tail.Link
Pivot
a.TailPivot
b.Tail.Link
Pivot
b.TailPivot
end {SetupAfter Setup has been executed, the leading node of smallest value in either list can be shifted by:
procedure GetLeader {O(1)
if a.Head.Key
b.Head
.Key
then Tempa.Head
a.Heada.Head
.Link
else Tempb.Head
b.Headb.Head
.Link
endif
Temp.Link
NIL
c.Tail.Link
Temp
c.TailTemp
end {GetLeaderWith these tools, the merge is:
function ListMerge(a,b) {O(n)
Setup
while a.Headb.Head do
GetLeader
endwhile
c.HeadPivot
.Link
return c
end {ListMergeIn practice, GetLeader would not be a called procedure; it is a shorthand reference to code that is incorporated at the point mentioned.
S.2 Binary Merge
Sometimes one list (say b) is much smaller than the other (a) with which it is to be merged. Suppose the lists are stored in arrays a[1 . . N] and b[1 . . M], sorted in nondecreasing order, and they are to be merged into an array c[1 . . NM], where NM = N + M.
The general idea of binary merge is that since N is much larger than M, entire segments of a tend to fall between values of b. The search for the possible position of a b-value is localized to a small segment of a that is searched by the method of binary search to determine an interval of a that can be moved to c. It is convenient to extend a with a sentinel value in a[0] and then to load c from right to left.
A value b[i] is compared with a segment of a of length Size: a[Left .. Right]. If b[i] < a[Left], then the entire segment of a can be moved to c. If not, the segment is searched with a tailored version of binary search for the largest index s such that: a[s] < b[i]. The subsequence b[i],a[s + 1] ,a[s + 2] ,...,a[Right] can then be moved into c. In either case, a new segment of a is chosen for testing against the (possibly) new value b[i].
The move operation is:
procedure Move(x,y) {O(y - x)
for z = y downto x do
c[k]a[z]
kk - 1
next z
end {Move
An effective search segment size is one less than the largest power of 2 less than (N/M). It can be determined by Size  Power(N/M) - 1, using:
Power(N/M) - 1, using:
function Power(x) {O(ln x)
PX1
while PXx do
PXPX X 2
endwhile
return (PX DIV 2)
end {PowerThe initialization procedure is:
procedure Setup {O(1)
if a[1] < b[1]
then Sentinela[1] - 1
else Sentinelb[1] - 1
endif
a[0]Sentinel
SizePower(N / M) - 1
iM
kN X M
end {SetupThe merge operation is then:
procedure BinaryMerge {O(n 1n n)
Setup
while i1 do
if b[i] < a[Left]
then Move(Left,Right)
RightLeft - 1
else sBinSearch(b[i],Left,Right)
Move(s + 1,Right)
Rights
c[k]b[i]
kk - 1
ii - 1
endif
LeftRight - Size
if Left < 0 then Left0 endif
endwhile
end {BinaryMerge
S.3 Merge Sorting
The simplest form of sorting routine based on merging sorts an array, a, with the help of an array, b, of the same size. Segments in one array are merged into the other. The segments are initially of length one and are increased in size from one pass of the routine to another until one of them contains the entire file. It is convenient to make passes back and forth between the arrays. The merging procedures of the previous sections do not work unmodified, partly because sentinel records would need to be placed in the middle of a file.
A utility routine used in the merge that copies a segment of one array into another is:
procedure Copy, (a,x,y,b,z) {O(y - x)
for dex = x to y do
b[z]a[dex]
zz +1
next dex
end {CopyWith the help of Copy, the basic merge operation is:
procedure TailMerge(a,L,M,R,b) {O(R - L)
iL
kL
jM + 1
while iM AND j
R do
if a[i]a[j]
then b[k]a[i]
ii + 1
else b[k]a[j]
jj + 1
endif
kk + 1
endwhile
if i > M
then Copy(a,j,R,b,k)
else Copy(a,i,M,b,k)
endif
end {TailMergeNow one phase (pass) is of the form:
procedure Phase(a,b,Size) {O(N)
s1
while s(N - 2 * Size - 1) do
TailMerge(a,s,s + Size - 1,s + 2 * Size - 1,b)
ss + 2 * Size
endwhile
if (s + Size - 1) < N
then TailMerge(a,s,s + Size - 1,N,b)
else Copy(a,s,N,b,s)
endif
end {PhaseThe sort then becomes a repetition of phases:
procedure MergeSort {O(N 1n N)
Size1
while Size < N do
Phase(a,b,Size)
Size2 * Size
Phase(b,a,Size)
Size2 * Size
endwhile
end {MergeSort
Programs
Programs for trying it yourself
PGS.1 Write a program that creates two linked lists, sorts them, displays them, merges them with ListMerge, and displays the resulting list.
PGS.2 Write a program that initializes two arrays to be sorted--one eight times larger than the other--sorts them, merges them with BinaryMerge, and displays the result.
PGS.3 Implement MergeSort.


