The procedure QuickSort acts on a sequence of keys, assumed to be in array Key[Low . . High]. It repeatedly establishes Property P(k)
Key[i]
Key[k]
for some k, until the set of keys Key[Low]
The value of Key[k] is called the pivot, and its initial position within the subrange Key [Low] . . . Key [High] is called the PivotIndex. When P(k) has been established, k is the index of the (new) position of the pivot in the range Low
Two auxiliary routines are needed by QuickSort. Function FindPivot determines the pivot index (and returns 0 if all of the keys in the index subrange [Low . . High] are identical--hence, if Low = High). Procedure Partition establishes P(Last) in the index subrange [Low . . High]. (Last is the last candidate for k in the action of Partition.) With these routines:
It is tempting to look for clever pivot-selection strategies, but a simple one is fairly serviceable: choose the larger of the first two values within the subrange [Low . . High] that differ. The logic of this strategy is:
Another is: take the first one, Key[Low].
These strategies are helpful in a set with duplicate values, but are inefficient in a set that is already sorted. A better strategy is to choose a pivot at random from Key[Low . . High], but the machinery for choosing a random index is almost as complex as QuickSort itself unless it is available as a utility routine. The interested reader may consult section A and the program in section K.
When the pivot value has been determined, P(Last) may be developed within the subrange [Low . . High] by swapping values that are larger than pivot and have a smaller index, with values that are no larger than pivot and have a larger index. There are a number of ways to do the testing and swapping operations, but all involve a fundamental asymmetry because one test of values relative to Pivot is a strict inequality and the other is not.
The strategy used here is relatively simple to debug. The strategy starts with Last = Low + 1, and sweeps from Low + 1 to High, testing Key[dex] against Pivot. When Key[dex] < Pivot, it is swapped with Key[Last], and Last is incremented. Now Key[Last] (the new Last) may not be less than Pivot, but it will be swapped with the next such value encountered. This process creates a segment of values from Key[Low + 1] to Key[Last - 1] that are all smaller than Pivot. Finally, Key[Low] and Key[Last] (the very last) are swapped. In short:
QuickSort is faster on the average than the sorting techniques SelectionSort, BubbleSort, and InsertionSort discussed in Chapter 1, but not for very small or nearly sorted sets. A rough analysis is:
The operation likely to consume the most time is the exchange of records in Swap.
No element in Key[Low] . . . Key[High] is exchanged more than once during a call Partition(Last,Low,High,Pivot). Hence in terms of Swap units of time, Partition is O(High - Low + 1).
It is possible that Last = Low or Last = High, in which case one of the subranges at the next call contains High - Low elements. Hence in the worst case, Partition is called n times for a file of size n. Quicksort is thus 0(n2).
Partition tends to produce two new subranges, each with roughly half as many elements as are in [Low . . High]. Hence QuickSort tends to execute ln n levels, each acting on subranges of no more than n elements. Hence the average growth behavior of QuickSort is O(n ln n).
It is common to supplement QuickSort with a switch to InsertionSort for small subranges, a practice derived from experience.
Sorting algorithms with worst-case behavior O(n 1n n) are possible, and one such algorithm is discussed in section 8.6.1.
0.1 The QuickSort Demonstration Program
Key[k] for Low i k Key[j] for k j High Key[k] Key[High] is sorted. k High. QuickSort then calls upon itself to further arrange Key[Low] . . . Key[k - 1] and also Key[k + 1] . . . Key[High].procedure QuickSort(Low,High)
PivotIndex
FindPivot(Low,High)if PivotIndex
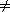0then Pivot
Key[PivotIndex]Partition(Last,Low,High,Pivot)
QuickSort(Low,Last - 1)
QuickSort(Last + 1,High)
endif
end {QuickSortfunction FindPivot(Low,High)
Value
Key[Low]for m = Low + 1 to High do
case
Key[m] > Value : return m
Key[m] < Value : return Low
endcase
next m
return 0
end {FindPivotprocedure Partition(Last,Low,High,Pivot)
Last
Lowfor dex = Low + 1 to High do
if Key[dex] < Pivot
then Last
Last + 1Swap(Last,dex)
endif
next dex
if Low
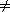Last then Swap(Low,Last) endifend {Partition0.1 The QuickSort Demonstration Program
PROGRAM QuickSortDemo(Input,Output);
CONST Max = 50;
TYPE KeyType = ARRAY [1 Max] OF INTEGER;
VAR Key : KeyType;
Swaps : INTEGER;
Tests : INTEGER;
Tail : INTEGER;
Done : BOOLEAN;
{ }PROCEDURE Preface;
BEGIN
Writeln('This program demonstrates the action of a');Writeln('QuickSort procedure. It accepts a sequence');Writeln('of up to ' ,Max,' non-negative integers, sorts');Writeln('them, and reports the number of comparisons');Writeln('and swaps needed to sort them.')END {Preface};{ }PROCEDURE Display(Low,High : INTEGER);
VAR m : INTEGER;
BEGIN
Writeln;
FOR m := Low TO High DO Write(Key[m] : 4);
Writeln;
Writeln(Swaps,' Swaps, ', Tests,' Comparisons')
END {Display};{ }PROCEDURE Setup(VAR Key : KeyType; VAR Tail : INTEGER);
VAR NonNeg : INTEGER;
BEGIN
Writeln('Enter values separated by blank spaces,');Writeln('terminating the sequence with a negative');Writeln('value.');Tail := 0 ;
Read(NonNeg);
WHILE (NonNeg >= 0) DO BEGIN
Tail := Tail + 1;
Key[Tail] := NonNeg;
Read(NonNeg)
END; Readln;
Swaps := 0; Tests := 0
END {Setup};{ }PROCEDURE RunAgain(VAR Done : BOOLEAN);
VAR ch : CHAR;
BEGIN
Write('If you wish to run again then enter Y, else N.');Readln(ch);
IF (ch = 'Y')
THEN Done := FALSE
ELSE Done := TRUE
END {RunAgain};{ }PROCEDURE QuicKSort(Low,High : INTEGER);
VAR PivotIndex : INTEGER;
Pivot : INTEGER;
Last : INTEGER;
{ }FUNCTION FindPivot(Low,High : INTEGER) : INTEGER;
BEGIN
IF (Low < High) {subject to modification}THEN FindPivot := Low
ELSE FindPivot := 0
END {FindPivot};{ }PROCEDURE Partition(VAR Last : INTEGER;
Low,High,Pivot : INTEGER);
VAR dex : INTEGER;
{ }PROCEDURE Swap(One,Two : INTEGER);
VAR Temp : INTEGER;
BEGIN
Temp := Key[One];
Key[One] := Key[Two];
Key[Two] := Temp;
Swaps := Swaps + 1
END {Swap};{ }BEGIN {Partition}Last := Low;
FOR dex := Low + 1 TO High DO
IF Key[dex] < Pivot
THEN BEGIN
Last := Last + 1;
Swap(Last,dex)
END;
IF (Low <> Last) THEN Swap(Low,Last);
IF (High > Low) THEN Tests := Tests + High - Low
END {Partition};{ }BEGIN {QuickSort}PivotIndex := FindPivot(Low,High);
IF PivotIndex <> 0
THEN BEGIN
Pivot := Key[PivotIndex];
Partition(Last,Low,High,Pivot);
QuicKSort(Low,Last - 1);
QuicKSort(Last + 1,High)
END
END {QuicKSort};{ }BEGIN {QuicKSortDemo}Preface;
REPEAT
Setup(Key,Tail);
Display(1,Tail);
QuickSort(1,Tail);
Display(1,Tail);
RunAgain(Done)
UNTIL Done
END {QuickSortDemo}.