M 1 2 3 4
1 1 0 0 0
2 1 1 0 1 n by n for n = 4
3 0 1 0 0
4 1 0 0 0
This matrix is represented as an OL (Orthogonal List) structure in section 6.5. Its cells can also be represented by an interwoven collection of circular lists where there is one value node for each nonempty cell, one braid for each row, one braid for each column, and a header node for each possible index. The value nodes can be represented in the form:
CellType = RECORD
Braid[1]:.CellType {row
Braid[2]:.CellType {column
Dim[1]: INTEGER {row index
Dim[2]: INTEGER {column index
END
The header node for index k contains a subnode of CellType that is on both the kth row braid and the kth column braid. As shown in Figure N.1, the header nodes themselves are linked into a double linear list:
HeadType = RECORD
Junction : Cell Type
Forth :HeadType {row
Back :HeadType {column
END {HeadTypeWhen the links for the first column and the third row are added to this picture, the result is as shown in Figure N.2. Figure N.3 shows the result when all of the links for the example are in place. (See pages 446 and 447.) The value nodes are linked into the header structure, as shown in Figure N.4 on page 448. This structure is an MDC, for Main Diagonal Circulation Sparse Matrix.
In an MDC, header nodes can account for roughly half of the nodes in the structure. For example, a 100 X 100 matrix with 117 value nodes out of 10,000 possible nodes will also use 100 header nodes. For comparison, if the data field is a pointer, OL of section 6.5 would require space for 317 nodes of CeIlType and MDC would require the equivalent of 257.
The list of headers can also be treated as sparse, with headers only for nonempty rows and columns; but deletion and insertion become somewhat more complex. The basic treatment given here can be modified as needed.
Both STORE and RETRIEVE involve finding the current header, then the predecessor of the node to be accessed. Header location for row or column dex is an adaptation of LT (section 3.3.2):
function FindIndex(dex)
pM.Head
while p.Junction.Dim[1] > dex do
pp
.Forth
endwhile
return p
end {FindIndexThe appropriate row and column can then be located by:
RowFindIndex(dex)
ColRow
With this minor change for determining Row and Col, the procedures FindPred, Retrieve, and Store of section 6.5 for structure OL apply to MDC as well.
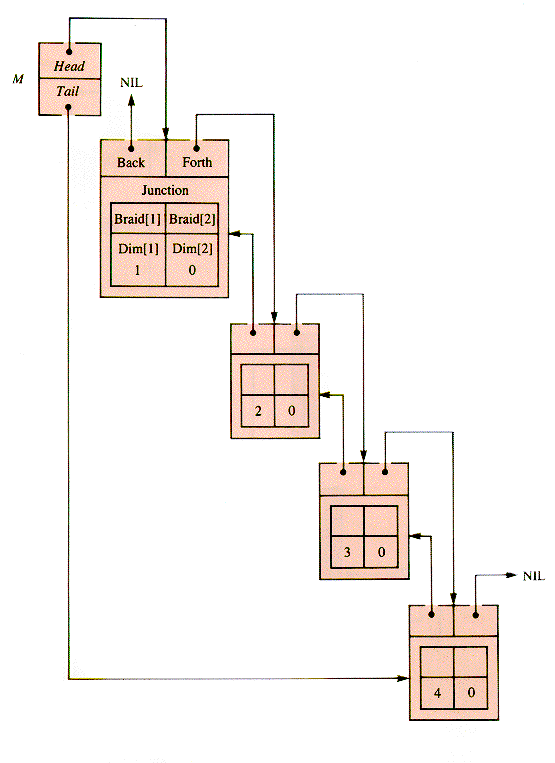
Figure N.1
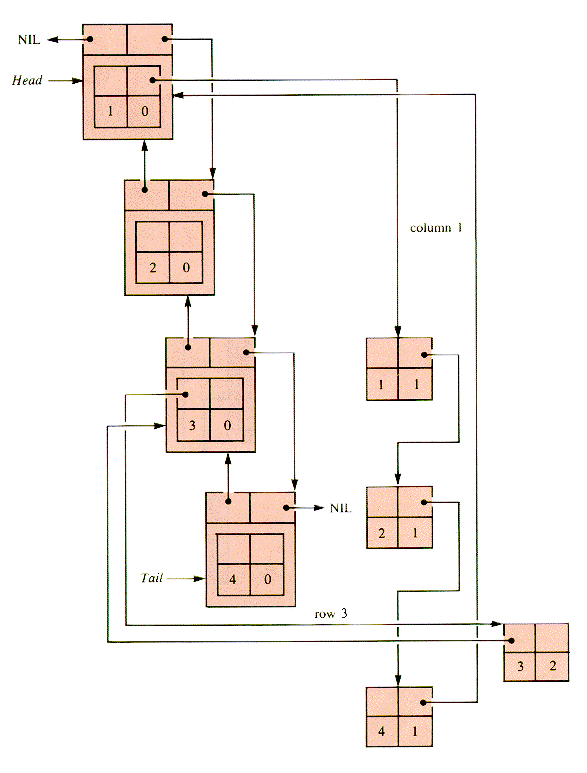
Figure N.2
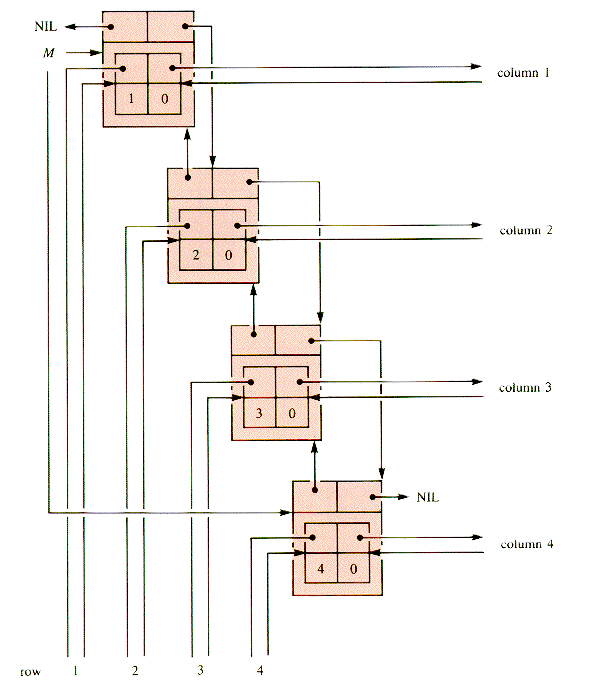
Figure N.3
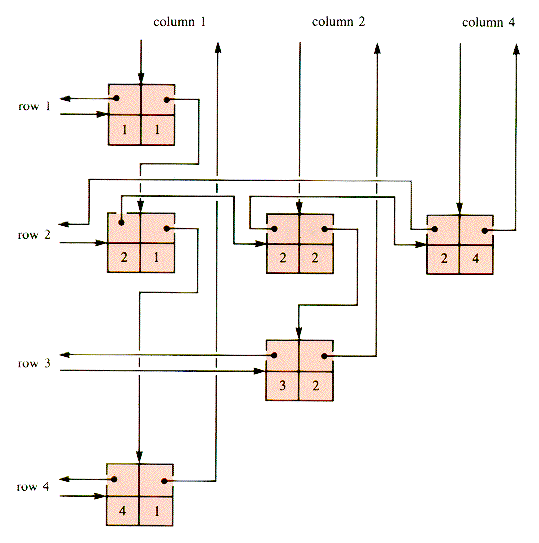
Figure N.4


