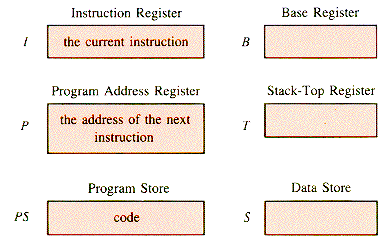
The information required to execute p-code instructions is contained in Figure G.1.
A p-code program is created and loaded into the program store PS by a p-code compiler (and loader, if that operation is separate). The PS is treated as a ROM (Read Only Memory) by the p-Machine. That is, no program ever alters it, but its contents are accessible. At the initiation of program execution, the program address register P is set to the address of the first (p-code) instruction in PS; and the machine automatically cycles through the following loop until the execution of an instruction (HALT or STOP, in effect) shuts off execution:
repeat {Execution cycle
1. Fetch the instruction at the address in P, and place it in I. (It will have a PS address.)
2. Increment P to point to the presumed next instruction.
3. Execute the instruction, i, in I.
if i is HALT then exit.
if i is an unconditional branch, or a conditional branch with a TRUE condition, then update P to the branch address.
forever
The instruction set is chosen with regard to the properties of the hardware that can be built to carry out the cycle, but there are many options. Because the p-Machine is a general-purpose computer, the chosen instruction-set embodies several standard functions:
1. I/0 (Input/Output)
2. Copy, to transfer data from one location to another
3. Arithmetic and logic
4. Branch
5. Conditional Branch
These functions help to define the instruction set, and so does the way instructions interact with the stack S. The stack interactions fundamentally determine the ability of p-code to support language features that supplement the actions listed above. The most crucial of such features are those associated with procedures. Procedures affect the p-Machine instructions to such an extent that they need to be discussed before the instruction set itself.
A data set is pushed onto S and popped from S in two ways--in many-valued segments and as individual values--in order to manage the data relevant to the execution of procedures. Such data can vary from one invocation to another of the same procedure. Data, and information about the location of data, can be passed to invoked procedures in a number of ways.
From the view of p-code, it is only necessary to know that a data set local to a particular invocation of a procedure is to be found in the data segment that represents that invocation. A value in a procedure invocation M is located by using the base address (which is in the base register B when M is being executed) and an offset, A, within the segment, that is specific to the variable. This process is illustrated in Figure G.2.
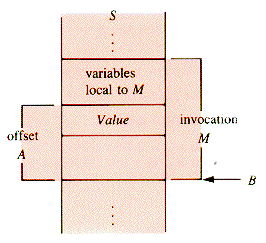
All data are local to one, and only one, procedure invocation. Consider, for example, the nested procedures below:
procedure Alpha
declare aVar
procedure Beta
declare b
procedure Gamma
declare c
.
.
.
aVar3 * b
.
.
.
end {Gamma
end {Beta
end {AlphaDuring execution of procedure Gamma, the stack S might appear as shown in Figure G.3.
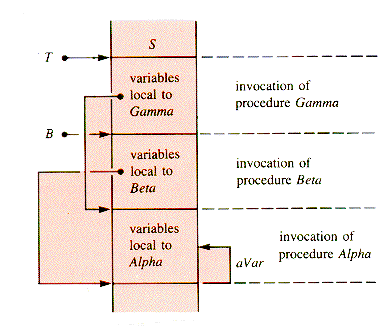
The dashed arrows imply that the segment to which the variable aVar belongs can be traced back through a sequence of base addresses--a linked list, in effect. Then aVar is located within its procedure invocation (of Alpha in this case). Clearly, some linking mechanism needs to be provided within the instruction format and the segments as they are stacked. The mechanism provided will even allow procedures to call themselves, directly or indirectly. For example, Gamma may refer to Gamma (directly) or to Beta (which may invoke Gamma again).
Because of the need for nested invocations of procedures, two links are provided in each segment. The segment scheme is shown in Figure G.4.
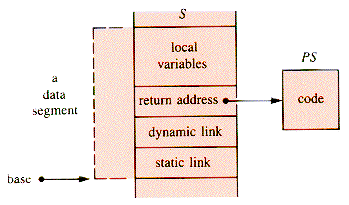
The static link points to the data segment of the immediately containing procedure (in the source code block structure). It is used to resolve variable references. In the example, the static link in an invocation of Gamma points to the base of an invocation of Beta.
The dynamic link is the address of the data segment of the calling (invoking) procedure. It is used to pop the segment off the stack at return time. In the most straightforward use of procedures, the dynamic link has the same value as the static link.
To determine the static link, the compiler keeps track of a level of declarations in the source code. Essentially this is the nesting level of the defining procedure. In the example, variables aVar, b, and c might be at levels 1, 2, and 3, respectively. The difference in levels between a variable and a segment that refers to it is precisely the number of times that the static link must be used to reach the segment in which the variable is declared. For example, to find the variable aVar at level 1 from procedure Gamma at level 3, the static links must be followed twice: to Beta, then to Alpha. Consequently, the address of a value in S consists of a level difference and an offset within a segment.
The behavior of the p-Machine does not entirely determine the syntax of p-code statements, but it certainly limits the options. In a simple, suitable format instructions contain three fields:
An instruction is written: INST L,A
The implication is that the pair (L,A) determines an address; but, for some instructions, the pair of fields has other uses. The syntax remains the same; the semantics varies.
A workable instruction set is the following:
This instruction set uses the stack S for transfers of control and data in sophisticated ways, but computation is confined to rather simple stack manipulations. For example, for operation code A = 2, execution of OPR is:
For A = 16, the execution is:
The OPR statement has seventeen variations:
Exercise EG.1 and problems PG.1 and PG.2 are appropriate at this point.
It may surprise you to discover how little of the complexity of this computing machine is generated by reading, writing, and arithmetic and how much by the flow of information and the flow of control. That is, however, true to the nature of computing.
The definitive exposition of p-code and the p-Machine is by the inventor [WIRTH, 1974], who includes a compiler of (limited) Pascal, PL/0, into p-code. The p-code concept has been extended to form the basis of compilers of full Pascal, notably at the University of California at San Diego. A further extension has brought forth machines that execute p-code directly in hardware.
Both FORTH (see section F) and the p-Machine are founded on stack management, but they are quite distinct. For example, only a few of the FORTH words come into play in p-code, and they are the familiar operations of arithmetic and logic. FORTH does not need a program store. Commands are interpreted and executed immediately. FORTH makes its stack the center of attention: the p-Machine uses its stack as a scaffold hidden behind the scenes of the high-level languages it supports.
Exercises immediate applications of the text material
EG.1 Convert the SUE segments that follow into p-code:
Problems not immediate, but requiring no major extensions of the text
PG.1 Write a p-code program that will input 10 numbers and print their sum.
PG.2 Choose one of the example problems EP2.1-EP2.5 of section 2.1 and solve it with a p-code program.
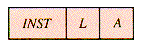
INST
instruction code {opcodeL
level differenceA
displacement {offsetLIT 0,A {Load the constant (literal) A onto the{top of the stack S: S[T] AOPR 0,A {Execute operation A. The possible{operations include I/O and arithmetic.LOD L,A {Push the value at address (L,A) onto{S. The address (L,A) is level difference{L, offset A.STO L,A {Pop the value of S and store it in (L,A).CAL L,A {Invoke a procedure, with first executable{statement at A in PS; start a new segment{with dynamic link set to the old B value,{and static link determined from L.INT 0,A {Increment T by A: T T + AJMP 0,A {Jump (transfer control) unconditionally{to the instruction at A in PS.JPC 0,A {If the top stack value, S[T], is zero,{then jump to A in PS; otherwise, don't.begin {additionT
T - 1S[T]
S[T] + S[T+1]end
begin {inputT
T + 1Readln(S[T])
end
OPR 0,0 {the last line of a programOPR 0,1 {unary minusOPR 0,2 {additionOPR 0,3 {subtractionOPR 0,4 {multiplicationOPR 0,5 {integer divisionOPR 0,6 {logical odd function--if S[T] is{odd, then replace it with TRUE(1),{else with FALSE(0)OPR 0,7 {no operator--used to debug programsOPR 0,8 {test for S[T--1] = S[T] and replace the{pair with TRUE(1) or FALSE(0)OPR 0,9 {test for 
OPR 0,10 {test for < i.e. S[T-1] < S[T]OPR 0,11 {test for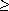 
OPR 0,12 {testfor >OPR 0,13 {test for 
OPR 0,14 {print S[T]OPR 0,15 {carriage returnOPR 0,16 {read into S[T]Exercises
i
1; Read(a,b)while i
10 do if a > bj
1 then a a + bwhile j
3 do Write(a,b)Write(i,j) else a
a - bj
j + 1 Write(a,b)endwhile endif
i
i + 1endwhile
i
1 i 1while i
10 do repeatWrite(i) Write(i)
i
i + 1 i 1endwhile until i > 10
i
1 Read(a)j
2 if a = 1k
4 then b 10while i
k do Write(a,b)if j < k endif
then j
j + 1 if a = 2Write(i,j,k) then b
20else k
k - 1 Write(a,b)Write(i,j,k) endif
endif if a = 3
i
i - 1 then b 20endwhile Write(a,b)
Write(i,j,k) endif
Problems