FORTH modules are normally built "bottom up" by defining an operation, called a word, that acts on the system stack, then extending that word to a more general or more powerful one, and so on, until the entire program is, in a word, a word. FORTH is extendable, because the language can be enlarged by the use of defining statements that enter words into a list called the dictionary. The words entered into the dictionary are then recognized as operations from which more words may be built.
FORTH is a threaded language as it is usually implemented, meaning that execution proceeds from the call of a routine (the execution of a word), which consists of calls to other routines, which in turn call others, and so on. At the lowest level the calls request use of the primitive operations known as machine instructions.
FORTH is an interpretative language as it is usually implemented, translating and then executing each word as it is encountered. Interpretation is perhaps a more natural partner of stack-oriented languages than of others, because each word performs some operation on the stack, immediately. The interpretative scheme in turn combines readily with an interactive system.
A FORTH statement, and the resulting interaction, is:
The user types 3 4 + . @ (@ means ''hit the RETURN key''), and FORTH responds 7 OK. (The underlining of the FORTH response is included for visual clarity in the text; it does not appear in actual output.) Table F. I shows the execution of this statement in terms of formal stack operations and SUE.
Similarly
has the effect on an initially empty stack that is shown in Figure F.1.
In general, FORTH reads tokens (separated by blank spaces) left to right, stacks operands, and executes words. In this context, arithmetic operators like "*" and "+" are built-in dictionary words. The definition of a word, say neword, is added to the dictionary by simply executing a statement of the form:
Here the OK response indicates that a new entry has been put into the dictionary.
Conversion of a length measured in inches to the corresponding length in centimeters can be defined by:
This defines intocm to be the sequence of operations:
Push 2.54 onto S.
Multiply the top two values, delete them, and push the product onto S; that is, execute the word "*".
The word intocm may then be used as any other word:
If the top value of the stack is 5 (however it got there):
Values may be stored in variables as well as on the stack. A variable identifier is bound to a memory cell (declared) when the connection between the two is established. For example
declares x as a variable, and x can then be assigned the value 10 by:
(The command "!'' is read ''store".) Retrieval of a variable value (to the stack) is done with "@", read "fetch". With the assignment above:
A redefinition of neword does not delete the old definition. When the word neword is encountered in the scan of a statement being interpreted, the latest definition is retrieved. It is possible to back up one definition of neword by execution of:
All dictionary entries made since neword are lost. In effect, the dictionary itself is treated as a stack with respect to the occurrences of a given word within it, as shown in Figure F.2. It is convenient to assume that a word, ''.S'', is available to display the stack contents, nondestructively.
If the stack contains 5 7 2, bottom to top, then:
A quirk (or astute design choice, if you like) is that access to the top of the FORTH stack is not just a TOP(S) operation but is essentially the operation pair [TOP(S), DELETE(S)], a pop. The use of the top value deletes it. Hence, to square the top value, for example, it is necessary first to duplicate it. A built-in word "DUP" is provided for this purpose. For example, if the stack contains: 5 7 - 2 then:
In terms of formal stack operations, DUP is INSERT(S,TOP(S)).
A number of stack manipulation words are contained in the basic dictionary of a FORTH compiler. The action of some of them is displayed here; their expression in terms of formal stack operations is left to the exercises and problems:
Exercise EF.1 and problem PF.1 are appropriate at this point.
The discussion of FORTH control structures in this section is very brief, but excellent treatments of FORTH are available for the reader interested in pursuing this topic further, including [BRODIE, 1981] and [BYTE, 1980].
The heart of any procedural language is the set of control structures it provides. It is necessary to have conditional branch statements in a language, and it is very awkward to do without explicit loops. Some peculiarities of control statements in FORTH are created by the way in which words are dealt with sequentially, in conjunction with an operation on the stack.
Everything in FORTH is postfix and stack-related, but the necessary structures are provided. For example
adds a word to the dictionary, which--when executed--plays the same role in program logic as the SUE statement
but it differs because it also manipulates the stack. A partial trace of its action is shown in Table F.2.
Similarly
adds a word to the dictionary, which--when executed--plays the role of the SUE statement:
Problem PF.2 and program PGF.1 are appropriate at this point.
Loop structures in FORTH are only slightly more complex.
A DO-loop is specified in FORTH by:
One such loop definition is:
When executed:
The index of the DO-loop is accessed within the loop by the FORTH word "I". With the help of the FORTH word "CR" that prints a carriage return:
Exercise EF.2 and Problem PF.3 are appropriate at this point.
Additional features of FORTH are described in [BRODIE, 1981] and [BYTE, 1980],
Exercises immediate applications of the text material
EF.1 Write procedures for stack operations to emulate the following FORTH words:
(PF. 1 asks for others.)
EF.2 What is the output of the following loop:
Problems not immediate, but requiring no major extensions of the text
PF.1 Write procedures, in terms of stack operations, that emulate the following FORTH words:
PF.2 Write a procedure for stack operations, to emulate the if . . . then . . . else construct in FORTH.
PF.3 Choose one of the example problems EP2. 1-EP2.5 of Chapter 2.1. Write a sequence of variable definitions and FORTH dictionary words with the property that the final word in the sequence solves the problem.
Programs for trying it yourself
PGF.1 Write a program that manages a stack on demand from an input file with FORTH commands. ".", ".S", and the commands of EF. 1 are a minimum viable set. If convenient, a special symbol may be used in place of linefeed. The "FORTH" response should be identical to that of the FORTH interpreter discussed in this section.
3 4 + 7 OK
Table F.1
Token Response Stack S
3 INSERT(S,3) V1 V2
Vt 3 4 INSERT(S,4) V1 V2
Vt 3 4 + begin
Sum
TOP(S) DELETE(S) V1 V2
Vt 3 Sum
Sum + TOP(S) DELETE(S) V1 V2
Vt INSERT(S,sum) V1 V2
Vt 7 end
Write(TOP(S))
2 3 4 + * 14 OK
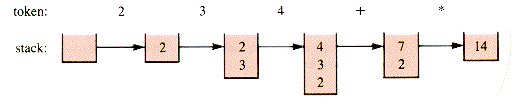
Figure F.1
: neword {details of what to do} ; OK: intocm 2.54 * ; OK
8 intocm 2032 OK
intocm 127 OK
VARIABLE x OK
10 x ! OK
x @ 10 OK
x @ intocm 254 OK
FORGE T neword OK
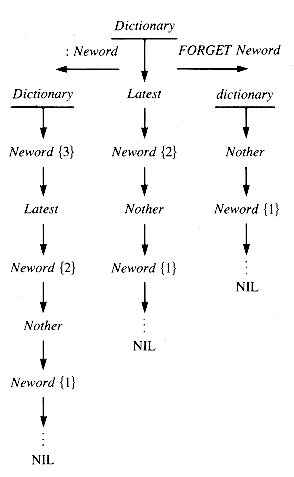
Figure F.2
S 5 7 2 OK
S 5 7 -2 OK
DUP S 5 7 -2 -2 OK
DUP * S 5 7 -2 4
S 5 7 2 OK
/MOD S 5 1 3 OK {remainder then quotient, of top{value division of next-to-topS 5 7 2 OK
MOD S 5 1 OK {remainder of top value division{of next-to-topS 5 7 2 OK
SWAP S 5 2 7 OK
S 5 7 2 OK
DUP S 5 7 2 2
S 5 7 2 OK
OVER S 5 7 2 7 OK {copy next-to-top and push itS 5 7 2 3 OK
ROT S 5 2 3 7 OK {cyclic rotation of the{top 3 valuesS 5 7 2 OK
DROP S 5 7 OK
S 1 5 7 2 OK
2SWAP S 7 2 1 5 OK {swaps top pairsS 5 7 2 OK
2DUP S 5 7 2 7 2 OK {duplicates top pairS 5 7 2 3 4 OK
20VER S 5 7 2 3 4 7 2 OK {copies second pair{and pushes itS 5 7 2 OK
2DROP S 5 OK {discards the top pairF.1 FORTH Control Structures
: Checkten 10 = IF Powwow THEN; OK
if TOP(S) = 10
then Powwow
endif
Table F.2
token operation
10 INSERT(S, 10)
= begin
t1
TOP(S) DELETE(S)
t2
TOP(S) DELETE(S)
if t1 = t2
then INSERT(S,1) {any value but 0 is else INSERT(S,0) {considered to be TRUE endif
end
IF bool
TOP(S) DELETE(S)
{The decision to execute or not to execute Powwow {is then, in effect, {if bool then Powwow endif: Spliten 10 = IF Powwow ELSE Wait THEN ; OK
if TOP(S) = 10
then Powwow
else Wait
endif
: DEF {limit} {index} DO {what you will} LOOP;:echo 5 to 1 DO . "shout " LOOP ; OK
echo shout shout shout shout shout OK
: echo2 3 to 1 DO CR . "shout " I LOOP ; OK
echo2
shout 1
shout 2
shout 3 OK
Exercises
MOD, /MOD, SWAP, DUP, DROP, OVER, 2DROP
:mystery 10 1 DO I * LOOP;
Problems
ROT , 2SWAP , 2DUP , 2OVER
Programs