A hash table differs from the array that provides storage for it because store and retrieve operations are specified by a key value rather than by an index and the number of legal keys is larger than the number of cells in the array. The operations of interest are STORE(Key) and RETRIEVE(Key). It is possible to simply store the key and retrieve a Boolean function that indicates the presence or lack of presence of the key in the table. This is the simple way to discuss hash tables, but it is more likely that the key is indeed just a key in a record containing a Value field or a pointer (or index) that addresses some bulk of information. In a word, hash tables are apt to be exogenous--directories to data stored external to them.
Note: For the sake of simpler exposition in this section, STORE(Key) assigns only a key value and RETRIEVE(Key) returns only the index of the location of Key in a table of keys. These are to be understood as surrogates for more realistic forms of the operations.
The function HF1 of section 2.5 simply converts letters to integers and sums them. It exhibits two of the properties needed to form a hash table:
HF1 transforms keys into integers.
HF1 possesses compression: the domain space defined by the set of all possible keys is much larger than the range space, the target table.
HF1 also exhibits an unhappy consequence of compression by hash functions:
In short:
Compression causes collisions.
The address functions of section 2.3 transform a domain value that is an n-tuple of the form
into a range value that is a single index in a one-dimensional table. The correspondence is one-to-one, and so there is no compression; but compression can be introduced much as it was for HF1. For example, a function HF2 can be defined by
If a key of any kind can be located in an n-dimensional table at
then HF2(t) provides the same service as for any n-dimensional table of keys as HF1 does for its specific data space.
Both HF1 and HF2 fail to define their range as a hash table structure by themselves because compression allows collisions: two elements of the domain can have identical range values. In any table structure, RETRIEVE must be the inverse of STORE, and so collisions must be resolved. With this in mind, the desired HASH TABLE structure consists of:
a domain
a range
a hash function h that exhibits compression
a resolution of the collisions caused by h
operations CREATE, STORE, and RETRIEVE
The domain is normally a given in a general sense and may be enormous. For example, it might be identifiers of up to 30 characters in length. The subset of the domain encountered in a specific application tends to be smaller but not well defined, and that makes a compressive system very attractive. CREATE requires no special attention. The range is a design decision that takes into account much of this section.
Suppose that a hash function is available that distributes the domain keys over the indices 0,1, . . . ,24 in a table HT with uniform probability. The first entry will not collide with any other. The probability that the second entry will not collide with a previous entry is 24/25. The probability that the third, fourth, . . . entries will not collide when entered is 23/25, 22/25, . . . (directly proportional to the number of free spaces). The probability that there will be no collisions for seven entries in a table of 25 cells is:
Hence the probability that there will be a collision is near 60 percent even though the table is less than one-third full. The cause is not really the small size of the table. (Figure out how likely a birthday collision is in a room containing 25 people.)
The ratio of n/m for n items in a table of size m is called the load factor,
The likelihood of collisions is increased if regularities in the domain keys affect the hash value. For example, a hash function based simply on the last letter of an identifier will map a lot of keys into wherever e, s, and n happen to go. (Try it on the words of the first two sentences of this paragraph.) Every part of a key should be involved--else, for example, the set {THEMES, THEME, THYME, TIME, CHIME, CHINA} will tend to collide. A hash function should tend to scatter natural clusters of the domain over the range.
The probability that a table location will be accessed is affected by two things:
the selection of elements from the potential set (the domain)
the transformation of the selected elements by the hash function into range indices
If this probability is not uniform, then there is said to be primary clustering. HF1 and HF2 are not particularly good hash functions. For one thing, all permutations of the same letters (or of the same indices) collide.
Although no hash function serves well in all circumstances, there are theoretical results that provide guidelines. One approach that can be recommended for integer values of z is
which satisfies 0
The size of the range table is chosen to be a prime number that is not close to a power of 2 (admittedly difficult for small tables).
To use the function h as a hash function first requires that the keys be turned into an integer in some efficient way. Keys are stored as binary strings in memory, and a binary string can be decoded as an integer (or sequence of integers) or converted with a utility function (such as ORD in Pascal). For the sake of illustration, consider the following simple approach applied to the ingredients of the recipe in section 2.5:
1. Ingredients are considered to be 12 characters in length, left-adjusted and padded with blank spaces.
2. Letters have as their index a two-digit value: A = 01, B = 02, . . ., Z = 26. Blanks have value 00. These values are found by a table lookup, which is much faster than calculation of them.
3. An ingredient is six four-digit integers. For example, BELLPEPPER is 0205, 1212, 1605, 1616, 0518, 0000.
4. The six integers for an ingredient are summed to form z. In functional terms, q(BELLPEPPER) = 5156 = z.
The calculation of q is much faster than it might appear to be. Let s[1 . . 12] be the string of characters of an ingredient. Then a calculation of z requires only one multiplication:
It is possible for z to be as large as 6 X 2626 = 15,756, but taking the sum MOD 10,000 restricts it to four digits (and more than that are unlikely anyway).
Now h(z) for BELLPEPPER, with m = 17 is:
For contrast, a second stage of multiplication by the prime base m can be introduced:
Both h and h2 can be easily determined with a hand calculator or a small program as a check on how well they work on a particular data set. Multiplication by 100 can be replaced with multiplication by a power of 2 and hence--in assembly languages--by shifts. There are a large number of possible variations of this scheme.
The results, for the 13 ingredients (including BROTH) and prime bases 17, 31, and 47, are shown in Table B.1 .
Collisions are produced by all of these functions, except h2 for the base of 47. In fact, that is a lucky accident. The loading factor for 13 items in a table of 47 items is 13/47 = 0.28. More importantly, the probability of no collisions with 13 items, no matter how randomly h2 scatters its key, is:
There is less than a 50/50 chance that ten pigeons can be placed at random in 47 pigeon holes without having two pigeons in one hole.
As the size of the table increases, the minimal loading factor with a chance of collision less than 50 percent shrinks. For m = 997 it is less than 4 percent.
Problem PB.1 is appropriate at this point.
The unavoidable conclusion is that any practical use of hash tables produces collisions. One way to implement collision resolution is a technique called linear probing.
Suppose a procedure Hash calculates an index k in a hash table HT[0 . . m - 1] for Key. If the table is empty, STORE(Key) would simply be HT[k]
If HT[k] is not empty, then another location must be chosen for Key, and it must be found again by RETRIEVE(Key). One simple strategy is to start looking at index k + 1, then k + 2, and so on until a free cell is located, or the table is exhausted without finding one. This is called linear probing.
A general probe function for a hash table begins with a starting index and the key value and returns an index. The return value is the index of the actual location of the key if it is found in HT, or the negative of that index if the table was searched to exhaustion. An appropriate empty slot for a STORE operation can then be located by probing with the null string Blank.
If the user of RetrieveHT(Key) is designed to interpret negative returns as "not there," then RetrieveHT may be replaced by Probe(Hash(Key), Key).
The effect of StoreHT can be illustrated with the use of m = 17, h, and the 13 ingredients in the example, entered in alphabetical order:
Problem PB.2 is appropriate at this point.
Two things about the sequence of HT entries are worth noting:
A different entry order stores some of the keys in different places. For the example, entry in reverse alphabetic order would place CUMIN in HT[10] and BELLPEPPER in HT[12].
Entries into HT[k] can increase the number of comparisons needed to store (or retrieve) items that hash to nearby indices, both smaller and larger. This is called secondary clustering as opposed to primary clustering in which distinct keys hash to the same index.
Secondary clustering can be alleviated to a certain extent (in tables with more room to maneuver than this example) by double hashing. This consists of skipping through the table from a collision in steps of
It is necessary for
A slight variation applicable to the example is to shift the four-digit values over one, and derive a new z, say z2. For example, z2 for BELLPEPPER would be
Or simply use 1 -
With q, Hash = h, HashAgain = h2, m = 31, and alphabetical entry order:
Actually there is one more collision than for
The number of collisions increases rapidly after the loading factor n/m reaches about 3/4, as can be seen by applying double hashing with h2 and m = 17. There is nowhere to go in a small table to escape collisions.
Problem PB.3 is appropriate at this point.
Deletion from a hash table is not merely a matter of replacing a key with the empty key, because a subsequent search may need to keep stepping past its cell into the sequence of stored entries with the same hash value. A deletion cell can be marked as available with some special value and used on a subsequent store that reaches it. (Since retrieval must continue past this point, separate Probe procedures are needed for store and retrieve operations.)
It is possible to devise an algorithm that rehashes a table. The number of deletions and the loading factor probably both affect the optimal point to do rehashing, which is not particularly efficient. It is probably just as well to make a linear sweep through the table and hash active keys into a new copy of the table, as long as there is room for two copies of the table in memory.
An alternate implementation of hash tables that permits deletion is based on the linked lists described in Chapter 3, and it is to be found in section L.
Problems not immediate, but requiring no major extensions of the text material
PB.1 Construct a table of hashed indices like the one of section B. 1 for the calendar months.
PB.2 Construct the hash table for the calendar months entered in calendar order, into a hash table of prime base m = 17.
PB.3 Construct the double-hashing table for the calendar months in calendar order with Hash = h, HashAgain = h2, and m = 31.
Programs for trying it yourself
PGB.1 Write a program that accepts identifiers of up to 12 characters in length, converts them to an integer with q, and stores them in a hash table HT with the use of Hash = h, HashAgain = h2, and m = 47. The program should report the number of collisions, the average number of tests by Probe, and the loading factor.
HF1(BROTH) = HF1(OLIVE)
[i1, i2, . . ., in]
HF2([i1, i2, . . ., in]) = (i1 +
+ in) MOD 25t = [i1, i2, . . ., in]
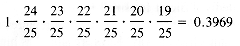
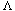. In this example, 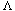= 7/25 = 0.28. Clearly, the probability of a collision increases with 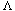.B.1 A Choice of Hash Functions
h(z) = INT(m(z
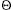MOD 1))
h(z) < m when 0 < 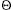< 1. The table indices addressed by h are 0 . . . m - 1. Suggested values of 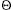are: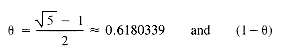
z
s[1] + s[3] + s[5] + s[7] + s[9] + s[11]z
z X 100 + s[2] + s[4] + s[6] + s[8] + s[10] + s[12]h(z) = INT(m(z
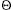MOD 1))= INT(17(5156
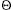MOD 1))= INT(17(3186.5827 MOD 1))
= INT(17(0.5827))
= INT(9.9059)
= 9
h2(z) = INT(m(m(z
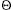MOD 1) MOD 1))= INT(17(9.9059 MOD 1))
= 15
Table B.1
m = 17 m = 31 m = 47
z h h2 h h2 h h2
-------------------------------------------
BEEF 0711 7 8 13 2 19 39
BELLPEPPER 5156 9 15 18 1 27 18
BLACKPEPPER 5342 9 2 16 20 25 11
BROTH 2538 9 11 17 20 26 37
CARROT 3639 0 7 0 24 1 8
CUMIN 3030 10 15 19 28 30 9
DILLWEED 2330 0 5 0 18 0 41
MUSHROOM 6557 7 10 13 27 21 3
OLIVE 2934 5 4 9 20 14 29
ONION 2443 14 9 26 17 40 12
POTATO 5631 2 9 4 18 6 46
SALT 3121 15 0 27 12 41 25
TOMATOPASTE 9352 14 8 26 13 40 4
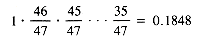
B.2 Linear Probing
Key. If it is not, HT[k] may already contain a key, and a collision occurs. The first task of a STORE operation is thus to determine if HT[k] is empty. For that purpose HT might be initialized with a value that cannot be a key or associated with a flag array. For the recipe example and most identifiers, HT may be initialized to null, blank, or empty strings.function Probe(Start,s) {O(m)i
Startrepeat
if HT[i] = s
then return i endif
i
(i + l) MOD muntil i = Start
return - i
end {Probeprocedure StoreHT(Key) {O(m)k
Hash(Key)dex
Probe(k,Blank)if dex < 0
then {deal with a full tableelse HT[dex]
Keyendif
end {StoreHTfunction RetrieveHT(Key) {O(m)k
Hash(Key)dex
Probe(k,Key)if dex < 0
then {report not thereelse return dex
endif
end {RetrieveHT m = 17
HT[7]
BEEF 0 CARROTHT[9]
BELLPEPPER 1 DILLWEEDHT[9] collision 2 POTATO
HT[10]
BLACKPEPPERHT[9] collision
HT[10] collision 5 OLIVE
HT[11]
BROTHHT[0]
CARROT 7 BEEFHT[10] collision 8 MUSHROOM
HT[11] collision 9 BELLPEPPER
HT[12] CUMIN 10 BLACKPEPPER
HT[0] collision 11 BROTH
HT[1]
DILLWEED 12 CUMINHT[7] collision
HT[8]
MUSHROOM 14 ONIONHT[5]
OLIVE 15 SALTHT[14]
ONION 16 TOMATOPASTEHT[2]
POTATOHT[15]
SALTHT[14] collision
HT[15] collision
HT[16]
TOMATOPASTEB.3 Secondary Clustering and Double Hashing
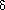, where 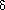depends on the key. In Probe, 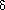was 1 for all keys, and a workable change is: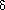 HashAgain(Key) followed within the search loop by: i (i + 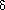) MOD m. 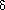to be relatively prime to m (else the search will be compromised). One way to guarantee that is to use Hash and HashAgain that satisfy:0
Hash(z) < m0
HashAgain(z) < mHash(z)
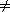HashAgain(z)2051 + 2121 + 6051 + 6160 + 5180 + 0000 = 21,563
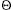in place of 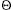, or use h2.HT[13]
BEEF m = 31HT[18]
BELLPEPPER 0 CARROTHT[16]
BLACKPEPPERHT[17]
BROTHHT[0]
CARROTHT[19]
CUMIN 4 POTAT0HT[0] collision 5 DILLWEED
HT[18] collision
HT[5]
DILLWEED (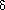 = 18)HT[13] collision 8 TOMATOPASTE
HT[9]
MUSHROOM (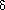 = 27) 9 MUSHROOMHT[9] collision
HT[29]
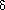OLIVE ( = 20)HT[26]
ONIONHT[4]
POTAT0 13 BEEFHT[27]
SALTHT[26] collision
HT[8]
TOMATOPASTE (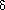 = 13) 16 BLACKPEPPER 17 BROTH
18 BELLPEPPER
19 CUMIN
26 ONION
27 SALT
29 OLIVE
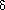= 1, but additional entries mapped into the range 16 - 19 by Hash are less likely to interfere with each other when their 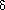s differ, because there is a good chance of skipping over the cluster.B.4 Deletion and Rehashing
Problems
Programs