



Over the years computer scientists have identified a number of general techniques that often yield effective algorithms in solving large classes of problems. This chapter presents some of the more important techniques, such as divide-and-conquer, dynamic programming, greedy techniques, backtracking, and local search. In trying to devise an algorithm to solve a given problem, it is often useful to ask a question such as "What kind of solution does divide-and-conquer, dynamic programming, a greedy approach, or some other standard technique yield?"
It should be emphasized, however, that there are problems, such as the NP-complete problems, for which these or any other known techniques will not produce efficient solutions. When such a problem is encountered, it is often useful to determine if the inputs to the problem have special characteristics that could be exploited in trying to devise a solution, or if an easily found approximate solution could be used in place of the difficult-to-compute exact solution.
Perhaps the most important, and most widely applicable, technique for designing efficient algorithms is a strategy called "divide-and-conquer." It consists of breaking a problem of size n into smaller problems in such a way that from solutions to the smaller problems we can easily construct a solution to the entire problem. We have already seen a number of applications of this technique, such as mergesort or binary search trees.
To illustrate the method consider the familiar "towers of Hanoi" puzzle. It consists of three pegs A, B, and C. Initially peg A has on it some number of disks, starting with the largest one on the bottom and successively smaller ones on top, as shown in Fig. 10.1. The object of the puzzle is to move the disks one at a time from peg to peg, never placing a larger disk on top of a smaller one, eventually ending with all disks on peg B.
One soon learns that the puzzle can be solved by the following simple algorithm. Imagine the pegs arranged in a triangle. On odd-numbered moves, move the smallest disk one peg clockwise. On even-numbered moves
Fig. 10.1. Initial position in towers of Hanoi puzzle.
make the only legal move not involving the smallest disk.The above algorithm is concise, and correct, but it is hard to understand why it works, and hard to invent on the spur of the moment. Consider instead the following divide-and-conquer approach. The problem of moving the n smallest disks from A to B can be thought of as consisting of two subproblems of size n - 1. First move the n - 1 smallest disks from peg A to peg C, exposing the nth smallest disk on peg A. Move that disk from A to B. Then move the n - 1 smallest disks from C to B. Moving the n-1 smallest disks is accomplished by a recursive application of the method. As the n disks involved in the moves are smaller than any other disks, we need not concern ourselves with what is below them on pegs A, B, or C. Although the actual movement of individual disks is not obvious, and hand simulation is hard because of the stacking of recursive calls, the algorithm is conceptually simple to understand, to prove correct and, we would like to think, to invent in the first place. It is probably the ease of discovery of divide-and-conquer algorithms that makes the technique so important, although in many cases the algorithms are also more efficient than more conventional ones.†
Consider the problem of multiplying two n-bit integers X and Y. Recall that the algorithm for multiplication of n-bit (or n-digit) integers usually taught in elementary school involves computing n partial products of size n and thus is an O(n2) algorithm, if we count single bit or digit multiplications and additions as one step. One divide-and-conquer approach to integer multiplication would break each of X and Y into two integers of n/2 bits each as shown in Fig. 10.2. (For simplicity we assume n is a power of 2 here.)
Fig. 10.2. Breaking n-bit integers into
![]() -bit pieces.
-bit pieces.
The product of X and Y can now be written
XY = AC2n + (AD+BC) 2n/2 +
BD (10.1)
If we evaluate XY in this straightforward way, we have to perform four multiplications of (n/2)-bit integers (AC, AD, BC, and BD), three additions of integers with at most 2n bits (corresponding to the three + signs in (10.1)), and two shifts (multiplication by 2n and 2n/2). As these additions and shifts take O(n) steps, we can write the following recurrence for T(n), the total number of bit operations needed to multiply n-bit integers according to (10.1).
T(1) = 1
T(n) = 4T(n/2) + cn (10.2)
Using reasoning like that in Example 9.4, we can take the constant c in (10.2) to be 1, so the driving function d(n) is just n, and then deduce that the homogeneous and particular solutions are both O(n2).
In the case that formula (10.1) is used to multiply integers, the asymptotic efficiency is thus no greater than for the elementary school method. But recall that for equations like (10.2) we get an asymptotic improvement if we decrease the number of subproblems. It may be a surprise that we can do so, but consider the following formula for multiplying X by Y.
XY = AC2n + [(A - B)(D - C) +
AC + BD]2n/2 + BD (10.3)
Although (10.3) looks more complicated than (10.1) it requires only three multiplications of (n/2)-bit integers, AC, BD, and (A - B)(D - C), six additions or subtractions, and two shifts. Since all but the multiplications take O(n) steps, the time T(n) to multiply n-bit integers by (10.3) is given by
T(1) = 1
T(n) = 3T(n/2) + cn
whose solution is T(n) = O(nlog23) = O(n1.59).
The complete algorithm, including the details implied by the fact that (10.3) requires multiplication of negative, as well as positive, (n/2)-bit integers, is given in Fig. 10.3. Note that lines (8)-(11) are performed by copying bits, and the multiplication by 2n and 2n/2 in line (16) by shifting. Also, the multiplication by s in line (16) simply introduces the proper sign into the result.
function mult ( X, Y, n: integer ): integer;
{ X and Y are signed integers £
2n.
n is a power of 2. The function returns XY }
var
s: integer; { holds the sign of XY }
m1, m2, m3: integer; { hold the three products }
A, B, C, D: integer; { hold left and right halves of X and Y }
begin
(1) s := sign(X) * sign(Y);
(2) X := abs(X);
(3) Y := abs(Y); { make X and Y positive }
(4) if n = 1 then
(5) if (X = 1) and (Y = 1) then
(6) return (s)
else
(7) return (0)
else begin
(8) A := left n/2 bits of X;
(9) B := right n/2 bits of X;
(10) C := left n/2 bits of Y;
(11) D := right n/2 bits of Y;
(13) m1 := mult(A, C, n/2);
(14) m2 := mult(A-B, D-C, n/2);
(15) m3 := mult(B, D, n/2);
(16) return (s * (m1*2n + (m1 +
m2 + m3) * 2n/2 + m3))
end
end; { mult }
Fig. 10.3. Divide-and-conquer integer multiplication algorithm.
Observe that the divide-and-conquer algorithm of Fig. 10.3 is asymptotically faster than the method taught in elementary school, taking O(n1.59) steps against O(n2). We may thus raise the question: if this algorithm is so superior why don't we teach it in elementary school? There are two answers. First, while easy to implement on a computer, the description of the algorithm is sufficiently complex that if we attempted to teach it in elementary school students would not learn to multiply. Furthermore, we have ignored constants of proportionality. While procedure mult of Fig. 10.3 is asymptotically superior to the usual method, the constants are such that for small problems (actually up to about 500 bits) the elementary school method is superior, and we rarely ask elementary school children to multiply such numbers.
The technique of divide-and-conquer has widespread applicability, not only in algorithm design but in designing circuits, constructing mathematical proofs and in other walks of life. We give one example as an illustration. Consider the design of a round robin tennis tournament schedule, for n = 2k players. Each player must play every other player, and each player must play one match per day for n -1 days, the minimum number of days needed to complete the tournament.
The tournament schedule is thus an n row by n -1 column table whose entry in row i and column j is the player i must contend with on the jth day.
The divide-and-conquer approach constructs a schedule for one- half of the players. This schedule is designed by a recursive application of the algorithm by finding a schedule for one half of these players and so on. When we get down to two players, we have the base case and we simply pair them up.
Suppose there are eight players. The schedule for players 1 through 4 fills the upper left corner (4 rows by 3 columns) of the schedule being constructed. The lower left corner (4 rows by 3 columns) of the schedule must pit the high numbered players (5 through 8) against one another. This subschedule is obtained by adding 4 to each entry in the upper left.
We have now simplified the problem. All that remains is to have lower-numbered players play high-numbered players. This is easily accomplished by having players 1 through 4 play 5 through 8 respectively on day 4 and cyclically permuting 5 through 8 on subsequent days. The process is illustrated in Fig. 10.4. The reader should now be able to generalize the ideas of this figure to provide a schedule for 2k players for any k.
In designing algorithms one is always faced with various trade-offs. One rule that has emerged is that it is generally advantageous to balance competing costs wherever possible. For example in Chapter 5 we saw that the 2-3 tree balanced the costs of searching with those of inserting, while more straightforward methods take O(n) steps either for each lookup or for each insertion, even though the other operation can be done in a constant number of steps.
Similarly, for divide-and-conquer algorithms, we are generally better off if the subproblems are of approximately equal size. For example, insertion sort can be viewed as partitioning a problem into two subproblems, one of size 1 and one of size n - 1, with a maximum cost of n steps to merge. This gives a recurrence
T(n) = T(1) + T(n - 1) + n
which has an O(n2) solution. Mergesort, on the other hand, partitions the
problems into two subproblems each of size n/2 and has O(nlogn)
performance. As a general principle, we often find that partitioning a problem into
Fig. 10.4. A round-robin tournament for eight players.
equal or nearly equal subproblems is a crucial factor in obtaining good performance.Often there is no way to divide a problem into a small number of subproblems whose solution can be combined to solve the original problem. In such cases we may attempt to divide the problem into as many subproblems as necessary, divide each subproblem into smaller subproblems and so on. If this is all we do, we shall likely wind up with an exponential-time algorithm.
Frequently, however, there are only a polynomial number of subproblems, and thus we must be solving some subproblem many times. If instead we keep track of the solution to each subproblem solved, and simply look up the answer when needed, we would obtain a polynomial-time algorithm.
It is sometimes simpler from an implementation point of view to create a table of the solutions to all the subproblems we might ever have to solve. We fill in the table without regard to whether or not a particular subproblem is actually needed in the overall solution. The filling-in of a table of subproblems to get a solution to a given problem has been termed dynamic programming, a name that comes from control theory.
The form of a dynamic programming algorithm may vary, but there is the common theme of a table to fill and an order in which the entries are to be filled. We shall illustrate the techniques by two examples, calculating odds on a match like the World Series, and the "triangulation problem."
Suppose two teams, A and B, are playing a match to see who is the first to win n games for some particular n. The World Series is such a match, with n = 4. We may suppose that A and B are equally competent, so each has a 50% chance of winning any particular game. Let P(i, j) be the probability that if A needs i games to win, and B needs j games, that A will eventually win the match. For example, in the World Series, if the Dodgers have won two games and the Yankees one, then i = 2, j = 3, and P(2, 3), we shall discover, is 11/16.
To compute P(i, j), we can use a recurrence equation in two variables. First, if i = 0 and j > 0, then team A has won the match already, so P(0, j) = 1. Similarly, P(i, 0) = 0 for i > 0. If i and j are both greater than 0, at least one more game must be played, and the two teams each win half the time. Thus, P(i, j) must be the average of P(i - 1, j) and P(i, j - 1), the first of these being the probability A will win the match if it wins the next game and the second being the probability A wins the match even though it loses the next game. To summarize:
P(i, j) = 1 if i = 0 and j > 0
= 0 if i > 0 and j = 0
= (P(i - 1, j) + P(i, j - 1))/2 if i > 0 and
j > 0 (10.4)
If we use (10.4) recursively as a function, we can show that P(i, j) takes no more than time O(2i+j). Let T(n) be the maximum time taken by a call to P(i, j), where i + j = n. Then from (10.4),
T(1) = c
T(n) = 2T(n - 1) + d
for some constants c and d. The reader may check by the means discussed in
the previous chapter that T(n) £ 2n-
1c + (2n-1-1)d, which is
O(2n) or
O(2i+j).
We have thus proven an exponential upper bound on the time
taken by
the recursive computation of P(i, j). However, to convince ourselves that the
recursive formula for P(i, j) is a bad way to compute it, we need to get a
big-omega lower bound. We leave it as an exercise to show that when we call
P(i, j), the total number of calls to P that gets made is
![]() , the number of
ways to choose i things out of i+j. If i = j, that number is
, the number of
ways to choose i things out of i+j. If i = j, that number is
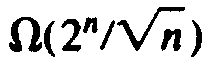 , where
n = i+j. Thus, T(n) is
, where
n = i+j. Thus, T(n) is
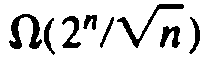 , and in fact, we can show it is
, and in fact, we can show it is
 also. While
also. While
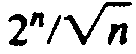 grows asymptotically more
slowly than 2n, the difference
is not great, and T(n) grows far too fast for the recursive calculation of P(i,
j)
to be practical.
grows asymptotically more
slowly than 2n, the difference
is not great, and T(n) grows far too fast for the recursive calculation of P(i,
j)
to be practical.
The problem with the recursive calculation is that we wind up computing the same P(i, j) repeatedly. For example, if we want to compute P(2, 3), we compute, by (10.4), P(1, 3) and P(2, 2). P(1, 3) and P(2, 2) both require the computation of P(1, 2), so we compute that value twice.
A better way to compute P(i, j) is to fill in the table suggested by Fig. 10.5. The bottom row is all 0's and the rightmost column all 1's by the first two lines of (10.4). By the last line of (10.4), each other entry is the average of the entry below it and the entry to the right. Thus, an appropriate way to fill in the table is to proceed in diagonals beginning at the lower right corner, and proceeding up and to the left along diagonals representing entries with a constant value of i+j, as suggested in Fig. 10.6. This program is given in Fig. 10.7, assuming it works on a two-dimensional array P of suitable size.
Fig. 10.5. Table of odds.
Fig. 10.6. Pattern of computation.
The analysis of function odds is easy. The loop of lines (4)-(5) takes
O(s) time, and that dominates the O(1) time for lines (2)-(3). Thus, the
outer loop takes time
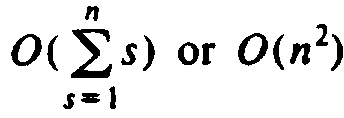 , where
i+j = n. Thus dynamic
, where
i+j = n. Thus dynamic
function odds ( i, j: integer ): real;
var
s, k: integer;
begin
(1) for s := 1 to i + j do begin
{ compute diagonal of entries whose indices sum to s }
(2) P[0, s] := 1.0;
(3) P[s, 0] := 0.0;
(4) for k := 1 to s-1 do
(5) P[k, s-k] := (P[k-1, s-k]
+ P[k, s-k-1])/2.0
end;
(6) return (P[i, j])
end; { odds }
Fig. 10.7. Odds calculation.
programming takes O(n2) time, compared with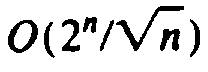 for the straightforward
approach. Since
for the straightforward
approach. Since
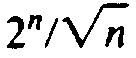 grows wildly faster than
n2, we would prefer dynamic
programming to the recursive approach under essentially any circumstances.
grows wildly faster than
n2, we would prefer dynamic
programming to the recursive approach under essentially any circumstances.
As another example of dynamic programming, consider the problem of triangulating a polygon. We are given the vertices of a polygon and a distance measure between each pair of vertices. The distance may be the ordinary (Euclidean) distance in the plane, or it may be an arbitrary cost function given by a table. The problem is to select a set of chords (lines between nonadjacent vertices) such that no two chords cross each other, and the entire polygon is divided into triangles. The total length (distance between endpoints) of the chords selected must be a minimum. We call such a set of chords a minimal triangulation.
Example 10.1. Figure 10.8 shows a seven-sided polygon and the (x, y)
coordinates of its vertices. The distance function is the ordinary Euclidean
distance. A triangulation, which happens not to be minimal, is shown by dashed
lines. Its cost is the sum of the lengths of the chords (v0,
v2), (v0, v3),
(v0, v5), and (v3,
v5), or
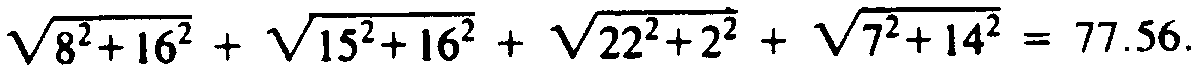 .
.
As well as being interesting in its own right, the triangulation problem has a number of useful applications. For example, Fuchs, Kedem, and Uselton [1977] used a generalization of the triangulation problem for the following purpose. Consider the problem of shading a two-dimensional picture of an object whose surface is defined by a collection of points in 3-space. The light source comes from a given direction, and the brightness of a point on the surface depends on the angles between the direction of light, the direction of the viewer's eye, and a perpendicular to the surface at that point. To estimate the direction of the surface at a point, we can compute a minimum triangulation
Fig. 10.8. A heptagon and a triangulation.
of the points defining the surface.Each triangle defines a plane in a 3-space, and since a minimum triangulation was found, the triangles are expected to be very small. It is easy to find the direction of a perpendicular to a plane, so we can compute the light intensity for the points of each triangle, on the assumption that the surface can be treated as a triangular plane in a given region. If the triangles are not sufficiently small to make the light intensity look smooth, then local averaging can improve the picture.
Before proceeding with the dynamic programming solution to the triangulation problem, let us state two observations about triangulations that will help us design the algorithm. Throughout we assume we have a polygon with n vertices v0, v1, . . . , vn-1, in clockwise order.
Fact 1. In any triangulation of a polygon with more than three vertices, every pair of adjacent vertices is touched by at least one chord. To see this, suppose neither vi nor vi+1† were touched by a chord. Then the region that edge (vi, vi+1) bounds would have to include edges (vi-1, vi), (vi+1, Vi+2) and at least one additional edge. This region then would not be a triangle.
Fact 2. If (vi, vj) is a chord in a triangulation, then there must be some vk such that (vi, vk) and (vk, vj) are each either edges of the polygon or chords. Otherwise, (vi, vj) would bound a region that was not a triangle.
To begin searching for a minimum triangulation, we pick two adjacent vertices, say v0 and v1. By the two facts we know that in any triangulation, and therefore in the minimum triangulation, there must be a vertex vk such that (v1, vk) and (vk, v0) are chords or edges in the triangulation. We must therefore consider how good a triangulation we can find after selecting each possible value for k. If the polygon has n vertices, there are a total of (n-2) choices to make.
Each choice of k leads to at most two subproblems, which we define to be polygons formed by one chord and the edges in the original polygon from one end of the chord to the other. For example, Fig. 10.9 shows the two subproblems that result if we select the vertex v3.
Fig. 10.9. The two subproblems after selecting v3.
Next, we must find minimum triangulations for the polygons of Fig. 10.9(a) and (b). Our first instinct is that we must again consider all chords emanating from two adjacent vertices. For example, in solving Fig. 10.9(b), we might consider choosing chord (v3, v5), which leaves subproblem (v0, v3, v5, v6), a polygon two of whose sides, (v0, v3) and (v3, v5), are chords of the original polygon. This approach leads to an exponential-time algorithm.
However, by considering the triangle that involves the chord (v0, vk) we never have to consider polygons more than one of whose sides are chords of the original polygon. Fact 2 tells us that, in the minimal triangulation, thechord in the subproblem, such as (v0, v3) in Fig. 10.9(b), must make a triangle with one of the other vertices. For example, if we select v4, we get the triangle (v0, v3, v4) and the subproblem (v0, v4, v5, v6) which has only one chord of the original polygon. If we try v5, we get the subproblems (v3, v4, v5) and (v0, v5, v6), with chords (v3, v5) and (v0, v5) only.
In general, define the subproblem of size s beginning at vertex vi, denoted Sis, to be the minimal triangulation problem for the polygon formed by the s vertices beginning at vi and proceeding clockwise, that is, vi, vi+1, ..., vi+s-1. The chord in Sis is (vi, vi+s-1). For example, Fig. 10.9(a) is S04 and Fig. 10.9(b) is S35. To solve Sis we must consider the following three options.
If we remember that "solving" any subproblem of size three or less requires no action, we can summarize (1)-(3) by saying that we pick some k between 1 and s-2 and solve subproblems Si,k+1 and Si+k,s-k. Figure 10.10 illustrates this division into subproblems.
Fig. 10.10. Division of Sis into subproblems.
If we use the obvious recursive algorithm implied by the above rules to solve subproblems of size four or more, then it is possible to show that each call on a subproblem of size s gives rise to a total of 3s-4 recursive calls, if we "solve" subproblems of size three or less directly and count only calls on subproblems of size four or more. Thus the number of subproblems to be solved is exponential in s. Since our initial problem is of size n, where n is the number of vertices in the given polygon, the total number of steps performed by this recursive procedure is exponential in n.
Yet something is clearly wrong in this analysis, because we know that besides the original problem, there are only n(n-4) different subproblems that ever need to be solved. They are represented by Sis, where 0 £ i < n and 4 £ s < n. Evidently not all the subproblems solved by the recursive procedure are different. For example, if in Fig. 10.8 we choose chord (v0, v3), and then in the subproblem of Fig. 10.9(b) we pick v4, we have to solve subproblem S44. But we would also have to solve this problem if we first picked chord (v0, v4), or if we picked (v1, v4) and then, when solving subproblem S45, picked vertex v0 to complete a triangle with v1 and v4.
This suggests an efficient way to solve the triangulation problem. We make a table giving the cost Cis of triangulating Sis for all i and s. Since the solution to any given problem depends only on the solution to problems of smaller size, the logical order in which to fill in the table is in size order. That is, for sizes s = 4, 5, . . . ,n-1 we fill in the minimum cost for problems Sis, for all vertices i. It is convenient to include problems of size 0 £ s < 4 as well, but remember that Sis has cost 0 if s < 4.
By rules (1)-(3) above for finding subproblems, the formula for computing Cis for s ³ 4 is:
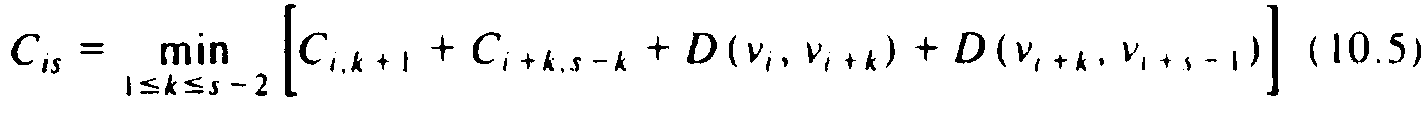
where D(vp, vq) is the length of the chord between vertices vp and vq, if vp and vq are not adjacent points on the polygon; D(vp, vq) is 0 if vp and vq are adjacent.
Example 10.2. Figure 10.11 holds the table of costs for Si,s for 0 £ i £ 6 and 4 £ s £ 6, based on the polygon and distances of Fig. 10.8. The costs for the rows with s < 3 are all zero. We have filled in the entry C07, in column 0 and the row for s = 7. This entry, like all in that row, represents the triangulation of the entire polygon. To see that, just notice that we can, if we wish, consider the edge (v0, v6) to be a chord of a larger polygon and the polygon of Fig. 10.8 to be a subproblem of this polygon, which has a series of additional vertices extending clockwise from v6 to v0. Note that the entire row for s = 7 has the same value as C07, to within the accuracy of the computation.
Let us, as an example, show how the entry 38.09 in the column for i = 6 and row for s = 5 is filled in. According to (10.5) the value of this entry, C65, is the minimum of three sums, corresponding to k = 1, 2, or 3. These sums are:
C62 + C04 + D
(v6, v0) + D(v0,
v3)
C63 + C13 + D
(v6, v1) + D(v1,
v3)
C64 + C22 + D
(v6, v2) + D(v2,
v3)
Fig. 10.11 Table of Cis's.
The distances we need are calculated from the coordinates of the vertices as:
D(v2, v3) =
D(v6, v0) = 0
(since these are polygon edges, not chords, and are present "for free")
D(v6, v2) = 26.08
D(v1, v3) = 16.16
D(v6, v1) = 22.36
D(v0, v3) = 21.93
The three sums above are 38.09, 38.52, and 43.97, respectively. We may conclude that the minimum cost of the subproblem S65 is 38.09. Moreover, since the first sum was smallest, we know that to achieve this minimum we must utilize the subproblems S62 and S04, that is, select chord (v0, v3) and then solve S64 as best we can; chord (v1, v3) is the preferred choice for that subproblem.
There is a useful trick for filling out the table of Fig. 10.11 according to the formula (10.5). Each term of the min operation in (10.5) requires a pair of entries. The first pair, for k = 1, can be found in the table (a) at the "bottom" (the row for s = 2)† of the column of the element being computed, and (b) just below and to the right‡ of the element being computed. The second pair is (a) next to the bottom of the column, and (b) two positions down and to the right. Fig. 10.12 shows the two lines of entries we follow to get all the pairs of entries we need to consider simultaneously. The pattern -- up the column and down the diagonal -- is a common one in filling tables during dynamic programming.
Fig. 10.12. Pattern of table scan to compute one element.
While Fig. 10.11 gives us the cost of the minimum triangulation, it does not immediately give us the triangulation itself. What we need, for each entry, is the value of k that produced the minimum in (10.5). Then we can deduce that the solution consists of chords (vi, vi+k), and (vi+k, vi+s-1) (unless one of them is not a chord, because k = 1 or k = s-2), plus whatever chords are implied by the solutions to Si,k+1 and Si+k,s-k. It is useful, when we compute an element of the table, to include with it the value of k that gave the best solution.
Example 10.3. In Fig. 10.11, the entry C07, which represents the solution to the entire problem of Fig. 10.8, comes from the terms for k = 5 in (10.5). That is, the problem S07 is split into S06 and S52; the former is the problem with six vertices v0, v1, . . . ,v5, and the latter is a trivial "problem" of cost 0. Thus we introduce the chord (v0, v5) of cost 22.09 and must solve S06.
The minimum cost for C06 comes from the terms for k = 2 in (10.5), whereby the problem S06 is split into S03 and S24. The former is the triangle with vertices v0, v1, and v2, while the latter is the quadrilateral defined by v2, v3, v4, and v5. S03 need not be solved, but S24 must be, and we must include the costs of chords (v0, v2) and (v2, v5) which are 17.89 and 19.80, respectively. We find the minimum value for C24 is assumed when k = 1 in (10.5), giving us the subproblems C22 and C33, both of which have size less than or equal to three and therefore cost 0. The chord (v3, v5) is introduced, with a cost of 15.65.
Fig. 10.13. A minimal cost triangulation.
Consider the problem of making change. Assume coins of values 25¢ (quarter), 10¢ (dime), 5¢ (nickel) and 1¢ (penny), and suppose we want to return 63¢ in change. Almost without thinking we convert this amount to two quarters, one dime and three pennies. Not only were we able to determine quickly a list of coins with the correct value, but we produced the shortest list of coins with that value.
The algorithm the reader probably used was to select the largest coin whose value was not greater than 63¢ (a quarter), add it to the list and subtract its value from 63 getting 38¢. We then selected the largest coin whose value was not greater than 38¢ (another quarter) and added it to the list, and so on.
This method of making change is a greedy algorithm. At any individual stage a greedy algorithm selects that option which is "locally optimal" in some particular sense. Note that the greedy algorithm for making change produces an overall optimal solution only because of special properties of the coins. If the coins had values 1¢, 5¢, and 11¢ and we were to make change of 15¢, the greedy algorithm would first select an 11¢ coin and then four 1¢ coins, for a total of five coins. However, three 5¢ coins would suffice.
We have already seen several greedy algorithms, such as Dijkstra's shortest path algorithm and Kruskal's minimum cost spanning tree algorithm. Dijkstra's shortest path algorithm is "greedy" in the sense that it always chooses the closest vertex to the source among those whose shortest path is not yet known. Kruskal's algorithm is also "greedy"; it picks from the remaining edges the shortest among those that do not create a cycle.
We should emphasize that not every greedy approach succeeds in producing the best result overall. Just as in life, a greedy strategy may produce a good result for a while, yet the overall result may be poor. As an example, we might consider what happens when we allow negative-weight edges in Dijkstra's and Kruskal's algorithms. It turns out that Kruskal's spanning tree algorithm is not affected; it still produces the minimum cost tree. But Dijkstra's algorithm fails to produce shortest paths in some cases.
Example 10.4. We see in Fig. 10.14 a graph with a negative cost edge between b and c. If we apply Dijkstra's algorithm with source s, we correctly discover first that the minimum path to a has length 1. Now, considering only edges from s or a to b or c, we expect that b has the shortest path from s, namely s ® a ® b, of length 3. We then discover that c has a shortest path from s of length 1.
Fig. 10.14. Graph with negative weight edge.
However, our "greedy" selection of b before c was wrong from a global point of view. It turns out that the path s ® a ® c ® b has length only 2, so our minimum distance of 3 for b was wrong.†
For some problems no known greedy algorithm produces an optimal solution, yet there are greedy algorithms that can be relied upon to produce "good" solutions with high probability. Frequently, a suboptimal solution with a cost a few percent above optimal is quite satisfactory. In these cases, a greedy algorithm often provides the fastest way to get a "good" solution. In fact, if the problem is such that the only way to get an optimal solution is to use an exhaustive search technique, then a greedy algorithm or other heuristic for getting a good, but not necessarily optimal, solution may be our only real choice.
Example 10.5. Let us introduce a famous problem where the only known algorithms that produce optimal solutions are of the "try-all-possibilities" variety and can have running times that are exponential in the size of the input. The problem, called the traveling salesman problem, or TSP, is to find, in an undirected graph with weights on the edges, a tour (a simple cycle that includes all the vertices) the sum of whose edge-weights is a minimum. A tour is often called a Hamilton (or Hamiltonian) cycle.
Figure 10.15(a) shows one instance of the traveling salesman problem, a graph with six vertices (often called "cities"). The coordinates of each vertex are given, and we take the weight of each edge to be its length. Note that, as is conventional with the TSP, we assume all edges exist, that is, the graph is complete. In more general instances, where the weight of edges is not based on Euclidean distance, we might find a weight of infinity on an edge that really was not present.
Figure 10.15(b)-(e) shows four tours of the six "cities" of Fig. 10.15(a). The reader might ponder which of these four, if any, is optimal. The lengths of these four tours are 50.00, 49.73, 48.39, and 49.78, respectively; (d) is the shortest of all possible tours.
Fig. 10.15. An instance of the traveling salesman problem.
The TSP has a number of practical applications. As its name implies, it can be used to route a person who must visit a number of points and return to his starting point. For example, the TSP has been used to route collectors of coins from pay phones. The vertices are the phones and the "home base." The cost of each edge is the travel time between the two points in question.
Another "application" of the TSP is in solving the knight's tour problem: find a sequence of moves whereby a knight can visit each square of the chessboard exactly once and return to its starting point. Let the vertices be the chessboard squares and let the edges between two squares that are a knight's move apart have weight 0; all other edges have weight infinity. An optimal tour has weight 0 and must be a knight's tour. Surprisingly, good heuristics for the TSP have no trouble finding knight's tours, although finding one "by hand" is a challenge.
The greedy algorithm for the TSP we have in mind is a variant of Kruskal's algorithm. Like that algorithm, we shall consider edges shortest first. In Kruskal's algorithm we accept an edge in its turn if it does not form a cycle with the edges already accepted, and we reject the edge otherwise. For the TSP, the acceptance criterion is that an edge under consideration, together with already selected edges,
Collections of edges selected under these criteria will form a collection of unconnected paths, until the last step, when the single remaining path is closed to form a tour.
In Fig. 10.15(a), we would first pick edge (d, e), since it is the shortest, having length 3. Then we consider edges (b, c), (a, b), and (e, f), all of which have length 5. It doesn't matter in which order we consider them; all meet the conditions for selection, and we must select them if we are to follow the greedy approach. Next shortest edge is (a, c), with length 7.08. However, this edge would form a cycle with (a, b) and (b, c), so we reject it. Edge (d, f) is next rejected on similar grounds. Edge (b, e) is next to be considered, but it must be rejected because it would raise the degrees of b and e to three, and could then never form a tour with what we had selected. Similarly we reject (b, d). Next considered is (c, d), which is accepted. We now have one path, a ® b ® c ® d ® e ® f, and eventually accept (a, f) to complete the tour. The resulting tour is Fig. 10.15(b), which is fourth best of all the tours, but less than 4% more costly than the optimal.
Sometimes we are faced with the task of finding an optimal solution to a problem, yet there appears to be no applicable theory to help us find the optimum, except by resorting to exhaustive search. We shall devote this section to a systematic, exhaustive searching technique called backtracking and a technique called alpha-beta pruning, which frequently reduces the search substantially.
Consider a game such as chess, checkers, or tic-tac-toe, where there are two players. The players alternate moves, and the state of the game can be represented by a board position. Let us assume that there are a finite number of board positions and that the game has some sort of stopping rule to ensure termination. With each such game, we can associate a tree called the game tree. Each node of the tree represents a board position. With the root we associate the starting position. If board position x is associated with node n, then the children of n correspond to the set of allowable moves from board position x, and with each child is associated the resulting board position. For example, Fig. 10.16 shows part of the tree for tic-tac-toe.
Fig. 10.16. Part of the tic-tac-toe game tree.
The leaves of the tree correspond to board positions where there is no move, either because one of the players has won or because all squares are filled and a draw resulted. We associate a value with each node of the tree.
First we assign values to the leaves. Say the game is tic-tac-toe. Then a leaf is assigned -l, 0 or 1 depending on whether the board position corresponds to a loss, draw or win for player 1 (playing X).The values are propagated up the tree according to the following rule. If a node corresponds to a board position where it is player 1's move, then the value is the maximum of the values of the children of that node. That is, we assume player 1 will make the move most favorable to himself i.e., that which produces the highest-valued outcome. If the node corresponds to player 2's move, then the value is the minimum of the values of the children. That is, we assume player 2 will make his most favorable move, producing a loss for player 1 if possible, and a draw as next preference.
Example 10.6. The values of the boards have been marked in Fig. 10.16. The leaves that are wins for O get value -1, while those that are draws get 0, and wins for X get + 1. Then we proceed up the tree. On level 8, where only one empty square remains, and it is X's move, the values for the unresolved boards is the "maximum" of the one child at level 9.
On level 7, where it is O's move and there are two choices, we take as a value for an interior node the minimum of the values of its children. The leftmost board shown on level 7 is a leaf and has value 1, because it is a win for X. The second board on level 7 has value min(0, -1) = -1, while the third board has value min(0, l) = 0. The one board shown at level 6, it being X's move on that level, has value max(l, -1, 0) = 1, meaning that there is some choice X can make that will win; in this case the win is immediate.
Note that if the root has value 1, then player 1 has a winning strategy. Whenever it is his turn he is guaranteed that he can select a move that leads to a board position of value 1. Whenever it is player 2's move he has no real choice but to select a moving leading to a board position of value 1, a loss for him. The fact that a game is assumed to terminate guarantees an eventual win for the first player. If the root has value 0, as it does in tic-tac-toe, then neither player has a winning strategy but can only guarantee himself a draw by playing as well as possible. If the root has value -1, then player 2 has a winning strategy.
The idea of a game tree, where nodes have values -1, 0, and l, can be generalized to trees where leaves are given any number (called the payoff) as a value, and the same rules for evaluating interior nodes applies: take the maximum of the children on those levels where player 1 is to move, and the minimum of the children on levels where player 2 moves.
As an example where general payoffs are useful, consider a complex game, like chess, where the game tree, though finite, is so huge that evaluating it from the bottom up is not feasible. Chess programs work, in essence, by building for each board position from which it must move, the game tree with that board as root, extending downward for several levels; the exact number of levels depends on the speed with which the computer can work. As most of the leaves of the tree will be ambiguous, neither wins, losses, nor draws, each program uses a function of board positions that attempts to estimate the probability of the computer winning in that position. For example, the difference in material figures heavily into such an estimation, as do such factors as the defensive strength around the kings. By using this payoff function, the computer can estimate the probability of a win after making each of its possible next moves, on the assumption of subsequent best play by each side, and chose the move with the highest payoff.†
Suppose we are given the rules for a game,† that is, its legal moves and rules for termination. We wish to construct its game tree and evaluate the root. We could construct the tree in the obvious way, and then visit the nodes in postorder. The postorder traversal assures that we visit an interior node n after all its children, whereupon we can evaluate n by taking the min or max of the values of its children, as appropriate.
The space to store the tree can be prohibitively large, but by being careful we need never store more than one path, from the root to some node, at any one time. In Fig. 10.17 we see the sketch of a recursive program that represents the path in the tree by the sequence of active procedure calls at any time. That program assumes the following:
type
modetype = (MIN, MAX)
function search ( B: boardtype; mode: modetype ): real;
{ evaluates the payoff for board B, assuming it is
player 1's move if mode = MAX and player 2's move
if mode = MIN. Returns the payoff }
var
C: boardtype; { a child of board B }
value: real; { temporary minimum or maximum value }
begin
(1) if B is a leaf then
(2) return (payoff(B))
else begin
{ initialize minimum or maximum value of children }
(3) if mode = MAX then
(4) value := -¥
else
(5) value := ¥;
(6) for each child C of board B do
(7) if mode = MAX then
(8) value := max(value, search(C, MIN))
else
(9) value := min(value, search(C, MAX));
(10) return (value)
end
end; { search }
Fig. 10.17. Recursive backtrack search program.
Another implementation we might consider is to use a nonrecursive program that keeps a stack of boards corresponding to the sequence of active calls to search. The techniques discussed in Section 2.6 can be used to construct such a program.
There is a simple observation that allows us to eliminate from consideration much of a typical game tree. In terms of Fig. 10.17, the for-loop of line (6) can skip over certain children, often many of the children. Suppose we have a node n, as in Fig. 10.18, and we have already determined that c1, the first of n's children, has a value of 20. As n is a max node, we know its value is at least 20. Now suppose that continuing with our search we find that d, a child of c2 has value 15. As c2, another child of n, is a min node, we know the value of c2 cannot exceed 15. Thus, whatever value c2 has, it cannot affect the value of n or any parent of n.
It is thus possible in the situation of Fig. 10.18, to skip consideration of the children of c2 that we have not already examined. The general rules for
Fig. 10.18. Pruning the children of a node.
skipping or "pruning" nodes involves the notion of final and tentative values for nodes. The final value is what we have simply been calling the "value." A tentative value is an upper bound on the value of a min node, or a lower bound on the value of a max node. The rules for computing final and tentative values are the following.Example 10.7. Consider the tree in Fig. 10.19. Assuming values for the leaves as shown, we wish to calculate the value for the root. We begin a postorder traversal. After reaching node D, by rule (2) we assign a tentative value of 2, which is the final value of D, to node C. We then search E and return to C and then to B. By rule (1), the final value of C is fixed at 2 and the value of B is tentatively set to 2. The search continues down to G and then back to F. The value F is tentatively set to 6. By rule (3), with p and q equal to F and B, respectively, we may prune H. That is, there is no need to search node H, since the tentative value of F can never decrease and it is already greater than the value of B, which can never increase.
Fig. 10.19. A game tree.
Continuing our example, A is assigned a tentative value of 2 and the search proceeds to K. J is assigned a tentative value of 8. L does not determine the value of max node J. I is assigned a tentative value of 8. The search goes down to N, and M is assigned a tentative value of 5. Node O must be searched, since 5, the tentative value of M, is less than the tentative value of I. The tentative values of I and A are revised, and the search goes down to R. Eventually R and S are searched, and P is assigned a tentative value of 4. We need not search T or below, since that can only lower P's value and it is already too low to affect the value of A.
Games are not the only sorts of "problems" that can be solved exhaustively by searching a complete tree of possibilities. A wide variety of problems where we are asked to find a minimum or maximum configuration of some sort are amenable to solution by backtracking search over a tree of all possibilities. The nodes of the tree can be thought of as sets of configurations, and the children of a node n each represent a subset of the configurations that n represents. Finally, the leaves each represent single configurations, or solutions to the problem, and we may evaluate each such configuration to see if it is the best solution found so far.
If we are reasonably clever in how we design the search, the children of a node will each represent far fewer configurations than the node itself, so we need not go to too great a depth before reaching leaves. Lest this notion of searching appear too vague, let us take a concrete example.
Example 10.8. Recall from the previous section our discussion of the traveling salesman problem. There we gave a "greedy algorithm" for finding a good but not necessarily optimum tour. Now let us consider how we might find the optimum tour by systematically considering all tours. One way is to consider all permutations of the nodes, and evaluate the tour that visits the nodes in that order, remembering the best found so far. The time for such an approach is O(n!) on an n node graph, since we must consider (n--1)! different permutations,† and each permutation takes O(n) time to evaluate.
We shall consider a somewhat different approach that is no better than the above in the worst case, but on the average, when coupled with a technique called "branch-and-bound" that we shall discuss shortly, produces the answer far more rapidly than the "try all permutations" method. Start constructing a tree, with a root that represents all tours. Tours are what we called "configurations" in the prefatory material. Each node has two children, and the tours that a node represents are divided by these children into two groups -- those that have a particular edge and those that do not. For example, Fig. 10.20 shows portions of the tree for the TSP instance from Fig. 10.15(a).
In Fig. 10.20 we have chosen to consider the edges in lexicographic order (a, b), (a, c), . . . ,(a, f), (b, c), . . . ,(b, f), (c, d), and so on. We could, of course pick any other order. Observe that not every node in the tree has two children. We can eliminate some children because the edges selected do not form part of a tour. Thus, there is no node for "tours containing (a, b), (a, c), and (a, d)," because a would have degree 3 and the result would not be a tour. Similarly, as we go down the tree we shall eliminate some nodes because some city would have degree less than 2. For example, we shall find no node for tours without (a, b), (a, c), (a, d), or (a, e).
Using ideas similar to those in alpha-beta pruning, we can eliminate far more nodes of the search tree than would be suggested by Example 10.8. Suppose, to be specific, that our problem is to minimize some function, e.g., the cost of a tour in the TSP. Suppose also that we have a method for getting a lower bound on the cost of any solution among those in the set of solutions represented by some node n. If the best solution found so far costs less than the lower bound for node n, we need not explore any of the nodes below n.
Example 10.9. We shall discuss one way to get a lower bound on certain sets of solutions for the TSP, those sets represented by nodes in a tree of solutions as suggested in Fig. 10.20. First of all, suppose we wish a lower bound on all solutions to a given instance of the TSP. Observe that the cost of any tour can be expressed as one half the sum over all nodes n of the cost of the two tour edges adjacent to n. This remark leads to the following rule. The sum
Fig. 10.20. Beginning of a solution tree for a TSP instance.
of the two tour edges adjacent to node n is no less than the sum of the two edges of least cost adjacent to n. Thus, no tour can cost less than one half the sum over all nodes n of the two lowest cost edges incident upon n.
For example, consider the TSP instance in Fig. 10.21. Unlike the instance in Fig. 10.15, the distance measure for edges is not Euclidean; that is, it bears no relation to the distance in the plane between the cities it connects. Such a cost measure might be traveling time or fare, for example. In this instance, the least cost edges adjacent to node a are (a, d), and (a, b), with a total cost of 5. For node b, we have (a, b) and (b, e), with a total cost of 6. Similarly, the two lowest cost edges adjacent to c, d, and e, total 8, 7, and 9, respectively. Our lower bound on the cost of a tour is thus (5+6+8+7+9)/2 = 17.5.
Fig. 10.21. An instance of TSP.
Now suppose we want a lower bound on the cost of a subset of tours defined by some node in the search tree. If the search tree is constructed as in Example 10.8, each node represents tours defined by a set of edges that must be in the tour and a set of edges that may not be in the tour. These constraints alter our choices for the two lowest-cost edges at each node. Obviously an edge constrained to be in any tour must be included among the two edges selected, no matter whether they are or are not lowest or second lowest in cost.† Similarly, an edge constrained to be out cannot be selected, even if its cost is lowest.
Thus, if we are constrained to include edge (a, e), and exclude (b, c), the two edges for node a are (a, d) and (a e), with a total cost of 9. For b we select (a b) and (b, e), as before, with a total cost of 6. For c, we cannot select (b, c), and so select (a, c) and (c, d), with a total cost of 9. For d we select (a, d) and (c, d), as before, while for e we must select (a, e), and choose to select (b, e). The lower bound for these constraints is thus (9+6+9+7+10)/2 = 20.5.
Now let us construct the search tree along the lines suggested in Example 10.8. We consider the edges in lexicographic order, as in that example. Each time we branch, by considering the two children of a node, we try to infer additional decisions regarding which edges must be included or excluded from tours represented by those nodes. The rules we use for these inference are:
When we branch, after making what inferences we can, we compute lower bounds for both children. If the lower bound for a child is as high or higher than the lowest cost tour found so far, we can "prune" that child and need not construct or consider its descendants. Interestingly, there are situations where the lower bound for a node n is lower than the best solution so far, yet both children of n can be pruned because their lower bounds exceed the cost of the best solution so far.
If neither child can be pruned, we shall, as a heuristic, consider the child
with the smaller lower bound first, in the hope of more rapidly reaching a
solution that is cheaper than the one so far found best.† After
considering one
child, we must consider again whether its sibling can be pruned, since a new
best solution may have been found. For the instance of Fig. 10.21, we get the
search tree of Fig. 10.22. To interpret nodes of that tree, it helps to
understand that the capital letters are names of the search tree nodes. The numbers
are the lower bounds, and we list the constraints applying to that node but
none of its ancestors by writing xy if edge (x, y) must be included and
![]() if
(x, y) must be excluded. Also note that the constraints introduced at a node
apply to all its descendants. Thus to get all the constraints applying at a node
we must follow the path from that node to the root.
if
(x, y) must be excluded. Also note that the constraints introduced at a node
apply to all its descendants. Thus to get all the constraints applying at a node
we must follow the path from that node to the root.
Lastly, let us remark that as for backtrack search in general, we construct the tree one node at a time, retaining only one path, as in the recursive algorithm of Fig. 10.17, or its nonrecursive counterpart. The nonrecursive version is probably to be preferred, so that we can maintain the list of constraints conveniently on a stack.
Example 10.10. Figure 10.22 shows the search tree for the TSP instance of
Fig. 10.21. To see how it is constructed, we begin at the root A of Fig.
10.22. The first edge in lexicographic order is (a, b), so we consider the two
children B and C, corresponding to the constraints ab and
![]() , respectively.
There is, as yet, no "best solution so far," so we shall consider both B and C
eventually.‡ Forcing (a b) to be included does not
raise the lower bound, but
excluding it raises the bound to 18.5, since the two cheapest legal edges for
nodes a and b now total 6 and 7, respectively, compared with 5 and 6 with no
constraints. Following our heuristic, we shall consider the descendants of
node B first.
, respectively.
There is, as yet, no "best solution so far," so we shall consider both B and C
eventually.‡ Forcing (a b) to be included does not
raise the lower bound, but
excluding it raises the bound to 18.5, since the two cheapest legal edges for
nodes a and b now total 6 and 7, respectively, compared with 5 and 6 with no
constraints. Following our heuristic, we shall consider the descendants of
node B first.
The next edge in lexicographic order is (a, c). We thus introduce children D and E corresponding to tours where (a, c) is included and excluded, respectively. In node D, we can infer that neither (a, d) nor (a, e) can be in a tour, else a would have too many edges incident. Following our heuristic we consider E before D, and branch on edge (a, d). The children F and G are introduced with lower bounds 18 and 23, respectively. For each of these children we know about three of the edges incident upon a, and so can infer something about the remaining edge (a, e).
Consider the children of F first. The first remaining edge in lexicographic order is (b, c). If we include (b, c), then, as we have included (a, b), we cannot include (b, d) or (b, e). As we have eliminated (a, e) and (b, e), we must have (c, e) and (d, e). We cannot have (c, d) or c and d would have three incident edges. We are left with one tour (a, b, c, e, d, a), whose cost is 23. Similarly, node I, where (b, c) is excluded, can be proved to represent only the tour (a b, e, c, d, a), of cost 21. That tour has the lowest cost found so far.
We now backtrack to E and consider its second child, G. But G has a lower bound of 23, which exceeds the best cost so far, 21. Thus we prune G. We now backtrack to B and consider its other child, D. The lower bound on D is 20.5, but since costs are integers, we know no tour represented by D can have cost less than 21. Since we already have a tour that cheap, we need not explore the descendants of D, and therefore prune D. Now we backtrack to A and consider its second child, C.
At the level of node C, we have only considered edge (a, b). Nodes J and K are introduced as children of C. J corresponds to those tours that have (a, c) but not (a, b), and its lower bound in 18.5. K corresponds to tours having neither (a, b) nor (a, c), and we may infer that those tours have (a, d) and (a, e). The lower bound for k is 21, and we may immediately prune k , since we already know a tour that is low in cost.
We next consider the children of J, which are L and M, and we prune M because its lower bound exceeds the best tour cost so far. The children of L are N and P, corresponding to tours that have (b, c), and that exclude (b, c). By considering the degree of nodes b and c, and remembering that the selected edges cannot form a cycle of fewer than all five cities, we can infer that nodes N and P each represent single tours. One of these, (a, c, b, e, d, a), has the lowest cost of any tour, 19. We have explored or pruned the entire tree and therefore end.
Fig. 10.22. Search tree for TSP solution.
Sometimes the following strategy will produce an optimal solution to a problem.
The method makes sense when we can restrict our set of transformations to a small set, so we can consider all transformations in a short time; perhaps O(n2) or O(n3) transformations should be allowed when the problem is of "size" n. If the transformation set is small, it is natural to view the solutions that can be transformed to one another in one step as "close." The transformations are called "local transformations," and the method is called local search.
Example 10.11. One problem we can solve exactly by local search is the minimal spanning tree problem. The local transformations are those in which we take some edge not in the current spanning tree, add it to the tree, which must produce a unique cycle, and then eliminate exactly one edge of the cycle (presumably that of highest cost) to form a new tree.
For example, consider the graph of Fig. 10.21. We might start with the tree shown in Fig. 10.23(a). One transformation we could perform is to add edge (d, e) and remove another edge in the cycle formed, which is (e, a, c, d, e). If we remove edge (a, e), we decrease the cost of the tree from 20 to 19. That transformation can be made, leaving the tree of Fig. 10.23(b), to which we again try to apply an improving transformation. One such is to insert edge (a, d) and delete edge (c, d) from the cycle formed. The result is shown in Fig. 10.23(c). Then we might introduce (a, b) and delete (b, c) as in Fig. 10.23(d), and subsequently introduce (b, e) in favor of (d, e). The resulting tree of Fig. 10.23(e) is minimal. We can check that every edge not in that tree has the highest cost of any edge in the cycle it forms. Thus no transformation is applicable to Fig. 10.23(e).
The time taken by the algorithm of Example 10.11 on a graph of n nodes and e edges depends on the number of times we need to improve the solution. Just testing that no transformation is applicable could take O(ne) time, since e edges must be tried, and each could form a cycle of length nearly n Thus the algorithm is not as good as Prim's or Kruskal's algorithms, but serves as an example where an optimal solution can be obtained by local search.
Local search algorithms have had their greatest effectiveness as heuristics for the solution to problems whose exact solutions require exponential time. A common method of search is to start with a number of random solutions, and apply the local transformations to each, until reaching a locally optimal solution, one that no transformation can improve. We shall frequently reach different locally optimal solutions, from most or all of the random starting solutions, as suggested in Fig. 10.24. If we are lucky, one of them will be
Fig. 10.23. Local search for a minimal spanning tree.
globally optimal, that is, as good as any solution.
In practice, we may not find a globally optimal solution as suggested in Fig. 10.24, since the number of locally optimal solutions may be enormous. However, we may at least choose that locally optimal solution that has the least cost among all those found. As the number of kinds of local transformations that have been used to solve various problems is great, we shall close the section with two examples -- the TSP, and a simple problem of "package placement."
The TSP is one for which local search techniques have been remarkably successful. The simplest transformation that has been used is called "2-opting." It consists of taking any two edges, such as (A, B) and (C, D) in Fig. 10.25, removing them, and reconnecting their endpoints to form a new tour. In Fig. 10.25, the new tour runs from B, clockwise to C, then along the edge (C, A), counterclockwise from A to D, and finally along the edge (D, B). If the sum of the lengths of (A, C) and (B, D) is less than the sum of the lengths of (A B) and (C, D), then we have an improved tour.† Note that we cannot
Fig. 10.24. Local search in the space of solutions.
connect A to D and B to C, as the result would not be a tour, but two disjoint cycles.
To find a locally optimal tour, we start with a random tour, and consider all pairs of nonadjacent edges, such as (A, B) and (C, D) in Fig. 10.25. If the tour can be improved by replacing these edges with (A, C) and (B, D), do so, and continue considering pairs of edges that have not been considered before. Note that the introduced edges (A, C) and (B, D) must each be paired with all the other edges of the tour, as additional improvements could result.
Example 10.12. Reconsider Fig. 10.21, and suppose we start with the tour of Fig. 10.26(a). We might replace (a, e) and (c, d), with a total cost of 12, by (a, d) and (c, e), with a total cost of 10, as shown in Fig. 10.26(b). Then we might replace (a, b) and (c, e) by (a, c) and (b, e), giving the optimal tour shown in Fig. 10.26(c). One can check that no pair of edges can be removed from Fig. 10.26(c) and be profitably replaced by crossing edges with the same endpoints. As one case in point, (b, c) and (d, e) together have the relatively high cost of 10. But (c, e) and (b, d) are worse, costing 14 together.
Fig. 10.25. 2-opting.
Fig. 10.26. Optimizing a TSP instance by 2-opting.
We can generalize 2-opting to k-opting for any constant k , where we remove up to k edges and reconnect the remaining pieces in any order so that result is a tour. Note that we do not require the removed edges to be nonadjacent in general, although for the 2-opting case there was no point in considering the removal of two adjacent edges. Also note that for k >2, there is more than one way to connect the pieces. For example, Fig. 10.27 shows the general process of 3-opting using any of the following eight sets of edges.

Fig. 10.27. Pieces of a tour after removing three edges.
It is easy to check that, for fixed k , the number of different k-opting transformations we need to consider if there are n vertices is O(n k). For example, the exact number is n(n-3)/2 for k = 2. The time taken to obtain a locally optimal tour may be considerably higher than this, however, since we could make many local transformations before reaching a locally optimum tour, and each improving transformation introduces new edges that may participate in later transformations that improve the tour still further. Lin and Kernighan [1973] have found that variable-depth-opting is in practice a very powerful method and has a good chance of getting the optimum tour on 40-100 city problems.
The one-dimensional package placement problem can be stated as follows. We have an undirected graph, whose vertices we call "packages." The edges are labeled by "weights," and the weight w(a, b) of edge (a, b) is the number of "wires" between packages a and b. The problem is to order the vertices p1, p2,..., pn, such that the sum of [i-j] w(pi, pj) over all pairs i and j is minimized. That is, we want to minimize the sum of the lengths of the wires needed to connect all the packages with the required number of wires.
The package placement problem has had a number of applications. For example, the "packages" could be logic cards on a rack, and the weight of an interconnection between cards is the number of wires connecting them. A similar problem comes up when we try to design integrated circuits from arrays of standard modules and interconnections between them. A generalization of the one-dimensional package placement problem allows placement of "packages," which have height and width, in a two-dimensional region, while minimizing the sum of the lengths of the wires between packages. This problem also has application to the design of integrated circuits, among other areas.
There are a number of local transformations we could use to find local optima for instances of the one-dimensional package placement problem. Here are several.
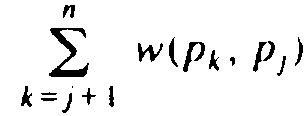 . Similarly, let R(j) be
. Similarly, let R(j) be
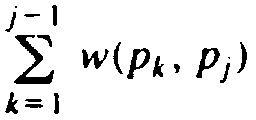 .
Improvement results if L(i) - R(i) + R(i+ 1) -
L(i+ 1) + 2w(pi,
pi+1) is
negative. The reader should verify this formula by computing the costs
before and after the interchange and taking the difference.
.
Improvement results if L(i) - R(i) + R(i+ 1) -
L(i+ 1) + 2w(pi,
pi+1) is
negative. The reader should verify this formula by computing the costs
before and after the interchange and taking the difference.Example 10.13. Suppose we take the graph of Fig. 10.21 to represent a package placement instance. We shall restrict ourselves to the simple transformation set (1). An initial placement, a, b, c, d, e, is shown in Fig. 10.28(a); it has a cost of 97. Note that the cost function weights edges by their distance, so (a, e) contributes 4x7 = 28 to the cost of 97. Let us consider interchanging d with e. We have L(d) = 13, R(d) = 6, L(e) = 24, and R(e) = 0. Thus L(d)-R(d)+R(e)- L(e)+2w(d, e) = -5, and we can interchange d and e to improve the placement to (a, b, c, e, d), with a cost of 92 as shown in Fig. 10.28(b).
In Fig. 10.28(b), we can interchange c with e profitably, producing Fig. 10.28(c), whose placement (a, b, e, c, d) has a cost of 91. Fig. 10.28(c) is locally optimal for set of transformations (1). It is not globally optimal; (a, c, e, d, b) has a cost of 84.
As with the TSP, we cannot estimate closely the time it takes to reach a local optimum. We can only observe that for set of transformations (1), there are only n-1 transformations to consider. Further, if we compute L(i) and R(i) once, we only have to change them when pi is interchanged with pi-1 or pi+1. Moreover, the recalculation is easy. If pi and pi+1 are interchanged, for example, then the new L(i) and R(i) are, respectively, L(i+1) - w(pi, pi+1) and R(i+1) + w(pi, pi+1). Thus O(n) time suffices to test for an improving transformation and to recalculate the L(i)'s and R(i)'s. We also need only O(n) time to initialize the L(i)'s and R(i)'s, if we use the recurrence
Fig. 10.28. Local optimizations.
L(1) = 0
L(i) = L(i-1) + w(pi-1, pi)
and a similar recurrence for R.
In comparison, the sets of transformations (2) and (3) each have O(n2) members. It will therefore take O(n2) time just to confirm that we have a locally optimal solution. However, as for set (1), we cannot closely bound the total time taken when a sequence of improvements are made, since each improvement can create additional opportunities for improvement.
| 10.1 | How many moves do the algorithms for moving n disks in the Towers of Hanoi problem take? | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| *10.2 | Prove that the recursive (divide and conquer) algorithm for the Tower of Hanoi and the simple nonrecursive algorithm described at the beginning of Section 10.1 perform the same steps. | ||||||||||||||||||||||||||
| 10.3 | Show the actions of the divide-and-conquer integer multiplication algorithm of Fig. 10.3 when multiplying 1011 by 1101. | ||||||||||||||||||||||||||
| *10.4 | Generalize the tennis tournament construction of Section 10.1 to tournaments where the number of players is not a power of two. Hint. If the number of players n is odd, then one player must receive a bye (not play) on any given day, and it will take n days, rather than n-1 to complete the tournament. However, if there are two groups with an odd number of players, then the players receiving the bye from each group may actually play each other. | ||||||||||||||||||||||||||
| 10.5 | We can recursively define the number of combinations of m things
out of n, denoted
|
||||||||||||||||||||||||||
| 10.6 | One way to compute the number of combinations of m things out of
n is to calculate (n)(n-1)(n-2) × × ×
(n-m+l)/(1)(2) × × × (m).
|
||||||||||||||||||||||||||
| 10.7 |
|
||||||||||||||||||||||||||
| 10.8 | The odds calculation of Fig. 10.7 requires O(n2) space. Rewrite the algorithm to use only O (n) space. | ||||||||||||||||||||||||||
| *10.9 | Prove that Equation (10.4) results in exactly
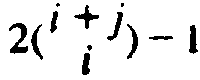 calls to P. calls to P. |
||||||||||||||||||||||||||
| 10.10 | Find a minimal triangulation for a regular octagon, assuming distances are Euclidean. | ||||||||||||||||||||||||||
| 10.11 | The paragraphing problem, in a very simple form, can be stated as follows: We are given a sequence of words w1, w2, . . . ,wk of lengths l1, l2, . . . ,lk, which we wish to break into lines of length L. Words are separated by blanks whose ideal width is b, but blanks can stretch or shrink if necessary (but without overlapping words), so that a line wi wi+1 ... wj has length exactly L. However, the penalty for stretching or shrinking is the magnitude of the total amount by which blanks are stretched or shrunk. That is, the cost of setting line wi wi+1 ... wj for j>i is (j-i) ½b'-b½, where b', the actual width of the blanks, is (L - li - li + 1- ...- lj)/(j-i). However, if j = k (we have the last line), the cost is zero unless b' < b, since we do not have to stretch the last line. Give a dynamic programming algorithm to find a least-cost separation of w1, w2, . . . ,wk into lines of length L. Hint. For i = k , k -1, . . ., 1, compute the least cost of setting wi , wi + 1, . . . ,wk. | ||||||||||||||||||||||||||
| 10.12 | Suppose we are given n elements x1, x2,. . .
,xn related by a linear
order x1 < x2 < · · · <
xn, and that we wish to arrange these
elements m in a binary search tree. Suppose that pi is the
probability
that a request to find an element will be for xi. Then for any given
binary search tree, the average cost of a lookup is
 ,
where di is the depth of the node holding
xi. Given the pi's, and
assuming the xi's never change, we can find a binary search tree that
minimizes the lookup cost. Find a dynamic programming algorithm
to do so. What is the running time of your algorithm? Hint.
Compute for all i and j the optimal lookup cost among all trees containing
only xi, xi +1, . . . , xi
+j-1, that is, the j elements beginning with xi. ,
where di is the depth of the node holding
xi. Given the pi's, and
assuming the xi's never change, we can find a binary search tree that
minimizes the lookup cost. Find a dynamic programming algorithm
to do so. What is the running time of your algorithm? Hint.
Compute for all i and j the optimal lookup cost among all trees containing
only xi, xi +1, . . . , xi
+j-1, that is, the j elements beginning with xi. |
||||||||||||||||||||||||||
| **10.13 | For what values of coins does the greedy change-making algorithm of Section 10.3 produce an optimal solution? | ||||||||||||||||||||||||||
| 10.14 |
|
||||||||||||||||||||||||||
| 10.15 | Describe a greedy algorithm for
Give an example where your algorithm does not produce an optimal answer, or show that no such example exists. |
||||||||||||||||||||||||||
| 10.16 | Give a nonrecursive version of the tree search algorithm of Fig. 10.17. | ||||||||||||||||||||||||||
| 10.17 | Consider a game tree in which there are six marbles, and players 1
and 2 take turns picking from one to three marbles. The player who
takes the last marble loses the game.
|
||||||||||||||||||||||||||
| *10.18 | Develop a branch and bound algorithm for the TSP based on the idea that we shall begin a tour at vertex 1, and at each level, branch based on what node comes next in the tour (rather than on whether a particular edge is chosen as in Fig. 10.22). What is an appropriate lower bound estimator for configurations, which are lists of vertices 1, v1, v2, . . . that begin a tour? How does your algorithm behave on Fig. 10.21, assuming a is vertex 1? | ||||||||||||||||||||||||||
| *10.19 | A possible local search algorithm for the paragraphing problem is to allow local transformations that move the first word of one line to the previous line or the last word of a line to the line following. Is this algorithm locally optimal, in the sense that every locally optimal solution is a globally optimal solution? | ||||||||||||||||||||||||||
| 10.20 | If our local transformations consist of 2-opts only, are there any locally optimal tours in Fig. 10.21 that are not globally optimal? |
There are many important examples of divide-and-conquer algorithms including the O(nlogn) Fast Fourier Transform of Cooley and Tukey [1965], the O(nlognloglogn) integer multiplication algorithm of Schonhage and Strassen [1971], and the O(n2.81) matrix multiplication algorithm of Strassen [1969]. The O(n1.59) integer multiplication algorithm is from Karatsuba and Ofman [1962]. Moenck and Borodin [1972] develop several efficient divide-and-conquer algorithms for modular arithmetic and polynomial interpolation and evaluation.
Dynamic programming was popularized by Bellman [1957]. The application of dynamic programming to triangulation is due to Fuchs, Kedem, and Uselton [1977]. Exercise 10.11 is from Knuth [1981]. Knuth [1971] contains a solution to the optimal binary search tree problem in Exercise 10.12.
Lin and Kernighan [1973] describe an effective heuristic for the traveling salesman problem.
See Aho, Hopcroft, and Ullman [1974] and Garey and Johnson [1979] for a discussion of NP-complete and other computationally difficult problems.
1. In the towers of Hanoi case, the divide-and-conquer algorithm is really the same as the one given initially.
†In what follows, we take all subscripts to be computed modulo n. Thus, in Fig. 10.8, vi and vi+1 could be v6 and v0, respectively, since n = 7.
†Remember that the table of Fig. 10.11 has rows of 0's below those shown.
‡By "to the right" we mean in the sense of a table that wraps around. Thus, if we are at the rightmost column, the column "to the right" is the leftmost column.
†In fact, we should be careful what we mean by "shortest path" when there are negative edges. If we allow negative cost cycles, then we could traverse such a cycle repeatedly to get arbitrarily large negative distances, so presumably we want to restrict ourselves to acyclic paths.
†Incidentally, some of the other things good chessplaying programs do are:
‡We should not imply that only "games" can be solved in this manner. As we shall see in subsequent examples, the "game" could really represent the solution to a practical problem.
†Note that we need not consider all n! permutations, since the starting point of a tour is immaterial. We may therefore consider only those permutations that begin with 1. †The rules for constructing the search tree will be seen to eliminate any set of constraints that cannot yield any tour, e.g., because three edges adjacent to one node are required to be in the tour.†An alternative is to use a heuristic to obtain a good solution using the constraints required for each child. For example, the reader should be able to modify the greedy TSP algorithm to respect constraints.
‡We could start with some heuristically found solution, say the greedy one, although that would not affect this example. The greedy solution for Fig. 10.21 has cost 21.
†Do not be fooled by the picture of Fig. 10.25. True, if lengths of edges are distances in the plane, then the dashed edges in Fig. 10.25 must be longer than those they replace. In general, however, there is no reason to assume the distances in Fig. 10.25 are distances in the plane, or if they are, it could have been (A B) and (C, D) that crossed, not (a C) and (B, D).