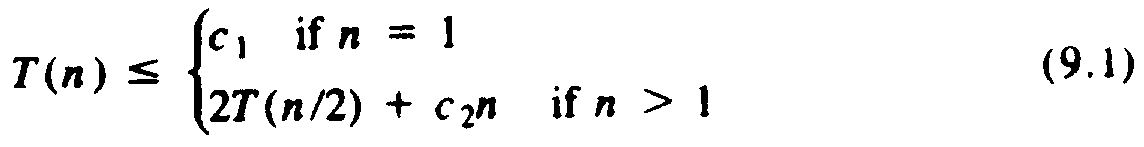



What is a good algorithm? There is no easy answer to this question. Many of the criteria for a good algorithm involve subjective issues such as simplicity, clarity, and appropriateness for the expected data. A more objective, but not necessarily more important, issue is run-time efficiency. Section 1.5 covered the basic techniques for establishing the running time of simple programs. However, in more complex cases such as where programs are recursive, some new techniques are needed. This short chapter presents some general techniques for solving recurrence equations that arise in the analysis of the running times of recursive algorithms.
One way to determine the run-time efficiency of an algorithm is to program it and measure the execution time of the particular implementation on a specific computer for a selected set of inputs. Although popular and useful, this approach has some inherent problems. The running times depend not only on the underlying algorithm, but also on the instruction set of the computer, the quality of the compiler, and the skill of the programmer. The implementation may also be tuned to work well on the particular set of test inputs chosen. These dependencies may become strikingly evident with a different computer, a different compiler, a different programmer, or a different set of test inputs. To overcome these objections, computer scientists have adopted asymptotic time complexity as a fundamental measure of the performance of an algorithm. The term efficiency will refer to this measure, and particularly to the worst-case (as opposed to average) time complexity.
The reader should recall from Chapter 1 the definitions of O(f(n)) and W(f(n)). The efficiency, i.e., worst-case complexity, of an algorithm is said to be O(f(n)), or just f(n) for short, if the function of n that gives the maximum, over all inputs of length n, of the number of steps taken by the algorithm on that input, is O(f(n)). Put another way, there is some constant c such that for sufficiently large n, cf(n) is an upper bound on the number of steps taken by the algorithm on any input of length n.
There is the implication in the assertion that "the efficiency of a given algorithm is f(n)" that the efficiency is also W(f(n)), so that f(n) is the slowest growing function of n that bounds the worst-case running time from above. However, this latter requirement is not part of the definition of O(f(n)), and sometimes it is not possible to be sure that we have the slowest growing upper bound.
Our definition of efficiency ignores constant factors in running time, and there are several pragmatic reasons for doing so. First, since most algorithms are written in a high level language, we must describe them in terms of "steps," which each take a constant amount of time when translated into the machine language of any computer. However, exactly how much time a step requires depends not only on the step itself, but on the translation process and the instruction repertoire of the machine. Thus to attempt to be more precise than to say that the running time of an algorithm is "on the order of f(n)", i.e., O(f(n)), would bog us down in the details of specific machines and would apply only to those machines.
A second important reason why we deal with asymptotic complexity and ignore constant factors is that the asymptotic complexity, far more than constant factors, determines for what size inputs the algorithm may be used to provide solutions on a computer. Chapter 1 discussed this viewpoint in detail. The reader should be alert, however, to the possibility that for some very important problems, like sorting, we may find it worthwhile to analyze algorithms in such detail that statements like "algorithm A should run twice as fast as algorithm B on a typical computer" are possible.
A second situation in which it may pay to deviate from our worst- case notion of efficiency occurs when we know the expected distribution of inputs to an algorithm. In such situations, average case analysis can be much more meaningful than worst case analysis. For example, in the previous chapter we analyzed the average running time of quicksort under the assumption that all permutations of the correct sorted order are equally likely to occur as inputs.
In Chapter 1 we showed how to analyze the running time of a program that does not call itself recursively. The analysis for a recursive program is rather different, normally involving the solution of a difference equation. The techniques for solving difference equations are sometimes subtle, and bear considerable resemblance to the methods for solving differential equations, some of whose terminology we borrow.
Consider the sorting program sketched in Fig. 9.1. There the procedure mergesort takes a list of length n as input, and returns a sorted list as its output. The procedure merge(L1, L2) takes as input two sorted lists L1 and L2, scans them each, element by element, from the front. At each step, the larger of the two front elements is deleted from its list and emitted as output. The result is a single sorted list containing the elements of L1 and L2. The details of merge are not important here, although we discuss this sorting algorithm in detail in Chapter 11. What is important is that the time taken by merge on lists of length n/2 is O(n).
function mergesort ( L: LIST; n: integer ): LIST;
{ L is a list of length n. A sorted version of L
is returned. We assume n is a power of 2. }
var
L1, L2: LIST
begin
if n = 1 then
return (L);
else begin
break L into two halves, L1 and L2,
each of length n/2;
return (merge (mergesort (L1,n/2),
mergesort(L2, n/2)));
end
end; { mergesort }
Fig. 9.1. Recursive procedure mergesort.
Let T(n) be the worst case running time of the procedure mergesort of Fig. 9.1. We can write a recurrence (or difference) equation that upper bounds T(n), as follows
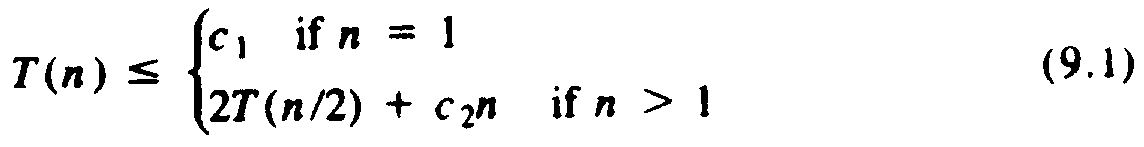
The term c1 in (9.1) represents the constant number of steps taken when L has length 1. In the case that n > 1, the time taken by mergesort can be divided into two parts. The recursive calls to mergesort on lists of length n/2 each take time T(n/2), hence the term 2T(n/2). The second part consists of the test to discover that n ¹ 1, the breaking of list L into two equal parts and the procedure merge. These three operations take time that is either a constant, in the case of the test, or proportional to n for the split and the merge. Thus the constant c2 can be chosen so the term c2n is an upper bound on the time taken by mergesort to do everything except the recursive calls. We now have equation (9.1).
Observe that (9.1) applies only when n is even, and hence it will provide an upper bound in closed form (that is, as a formula for T(n) not involving any T(m) for m < n) only if n is a power of 2. However, even if we only know T(n) when n is a power of 2, we have a good idea of T(n) for all n. In particular, for essentially all algorithms, we may suppose that T(n) lies between T(2i) and T(2i+1) if n lies between 2i and 2i+1. Moreover, if we devote a little more effort to finding the solution, we could replace the term 2T(n/2) in (9.1) by T((n+1)/2) + T((n-1)/2) for odd n > 1. Then we could solve the revised difference equation to get a closed form solution for all n.
There are three different approaches we might take to solving a recurrence equation.
This section examines the first two methods.
Example 9.1. Consider method (1) applied to Equation (9.1). Suppose we guess that for some a, T(n) = anlogn. Substituting n = 1, we see that this guess will not work, because anlogn has value 0, independent of the value of a. Thus, we might next try T(n) = anlogn + b. Now n = 1 requires that b ³ c1.
For the induction, we assume that
T(k) £ aklogk + b (9.2)
for all k < n and try to establish that
T(n) £ anlogn + b
To begin our proof, assume n ³ 2. From (9.1), we have
T(n) £ 2T(n/2)+c2n
From (9.2), with k = n/2, we obtain
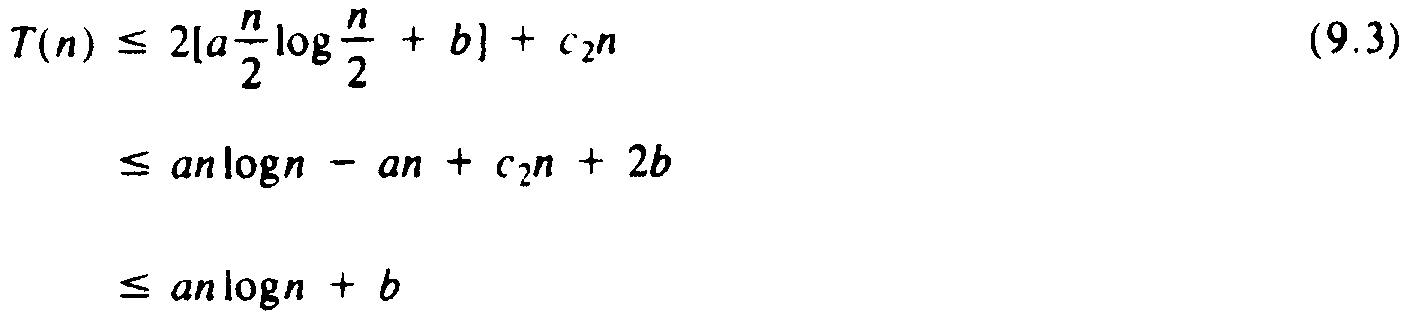
provided a ³ c2 + b.
We thus see that T(n) £ anlogn + b holds provided two constraints are satisfied: b ³ c1 and a ³ c2 + b. Fortunately, there are values we can choose for a that satisfy these two constraints. For example, choose b = c1 and a = c1 + c2. Then, by induction on n, we conclude that for all n ³ 1
T(n) £ (c1 + c2)nlogn + c1 (9.4)
In other words, T(n) is O(nlogn).
Two observations about Example 9.1 are in order. If we assume that T(n) is O(f(n)), and our attempt to prove T(n) £ cf(n) by induction fails, it does not follow that T(n) is not O(f(n)). In fact, an inductive hypothesis of the form T(n) £ cf(n) - 1 may succeed!
Secondly we have not yet determined the exact asymptotic growth rate for f(n), although we have shown that it is no worse than O(nlogn). If we guess a slower growing solution, like f(n) = an, or f(n) = anloglogn, we cannot prove the claim that T(n) £ f(n). However, the matter can only be settled conclusively by examining mergesort and showing that it really does take W(nlogn) time; in fact, it takes time proportional to nlogn on all inputs, not just on the worst possible inputs. We leave this observation as an exercise.
Example 9.1 exposes a general technique for proving some function to be an upper bound on the running time of an algorithm. Suppose we are given the recurrence equation
T(1) = c T(n) £ g(T(n/2), n), for n > 1 (9.5)
Note that (9.5) generalizes (9.1), where g(x, y) is 2x + c2y. Also observe that we could imagine equations more general than (9.5). For example, the formula g might involve all of T(n-1), T(n-2), . . . , T(1), not just T(n/2). Also, we might be given values for T(1), T(2), . . . , T(k), and the recurrence would then apply only for n > k. The reader can, as an exercise, consider how to solve these more general recurrences by method (1) -- guessing a solution and verifying it.
Let us turn our attention to (9.5) rather than its generalizations. Suppose we guess a function f(a1, . . . , aj, n), where a1, . . . , aj are parameters, and attempt to prove by induction on n that T(n) £ f(a1, . . . , aj, n). For example, our guess in Example 9.1 was f(a1, a2, n) = a1nlogn + a2, but we used a and b for a1 and a2. To check that for some values of a1, . . . , aj we have T(n) £ f(a1, . . . , aj, n) for all n ³ 1, we must satisfy
f(a1, . . . , aj, 1) ³ c f(a1, . . . , aj, n) ³ g(f(a1, . . . , aj, n/2), n) (9.6)
That is, by the inductive hypothesis, we may substitute f for T on the right side of the recurrence (9.5) to get
T(n) £ g(f(a1, . . . , aj, n/2), n) (9.7)
When the second line of (9.6) holds, we can combine it with (9.7) to prove that T(n) £ f(a1, . . . , an, n), which is what we wanted to prove by induction on n.
For example, in Example 9.1, we have g(x, y) = 2x + c2y and f(a1, a2, n) = a1nlogn + a2. Here we must try to satisfy
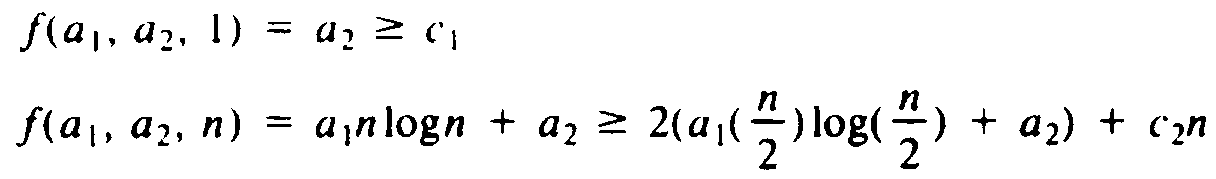
As we discussed, a2 = c1 and a1 = c1 + c2 is a satisfactory choice.
If we cannot guess a solution, or we are not sure we have the best bound on T(n), we can use a method that in principle always succeeds in solving for T(n) exactly, although in practice we often have trouble summing series and must resort to computing an upper bound on the sum. The general idea is to take a recurrence like (9.1), which says T(n) £ 2T(n/2) + c2n, and use it to get a bound on T(n/2) by substituting n/2 for n. That is
T(n/2) £ 2T(n/4) + c2n/2 (9.8)
Substituting the right side of (9.8) for T(n/2) in (9.1) yields
T(n) £ 2(2T(n/4) + c2n/2) + c2n = 4T(n/4) + 2c2n (9.9)
Similarly, we could substitute n/4 for n in (9.1) and use it to get a bound on T(n/4). That bound, which is 2T(n/8) + c2n/4, can be substituted in the right of (9.9) to yield
T(n) £ 8T(n/8)+3c2n (9.10)
Now the reader should perceive a pattern. By induction on i we can obtain the relationship
T(n) £ 2iT(n/2i)+ic2n (9.11)
for any i. Assuming n is a power of 2, say 2k, this expansion process comes to a halt as soon as we get T(1) on the right of (9.11). That will occur when i = k, whereupon (9.11) becomes
T(n) £ 2kT(1) + kc2n (9.12)
Then, since 2k = n, we know k = logn. As T(1) £ c1, (9.12) becomes
T(n) £ c1n + c2nlogn (9.13)
Equation (9.13) is actually as tight a bound as we can put on T(n), and proves that T(n) is O(nlogn).
Consider the recurrence that one gets by dividing a problem of size n into a subproblems each of size n/b. For convenience, we assume that a problem of size 1 takes one time unit and that the time to piece together the solutions to the subproblems to make a solution for the size n problem is d(n), in the same time units. For our mergesort example, we have a = b = 2, and d(n) = c2n/c1, in units of c1. Then if T(n) is the time to solve a problem of size n, we have
T(1) = 1 T(n) = aT(n/b) + d(n) (9.14)
Note that (9.14) only applies to n's that are an integer power of b, but if we assume T(n) is smooth, getting a tight upper bound on T(n) for those values of n tells us how T(n) grows in general.
Also note that we use equality in (9.14) while in (9.1) we had an inequality. The reason is that here d(n) can be arbitrary, and therefore exact, while in (9.1) the assumption that c2n was the worst case time to merge, for one constant c2 and all n, was only an upper bound; the actual worst case running time on inputs of size n may have been less than 2T(n/2) + c2n. Actually, whether we use = or £ in the recurrence makes little difference, since we wind up with an upper bound on the worst case running time anyway.
To solve (9.14) we use the technique of repeatedly substituting for T on the right side, as we did for a specific example in our previous discussion of expanding recurrences. That is, substituting n/bi for n in the second line of (9.14) yields
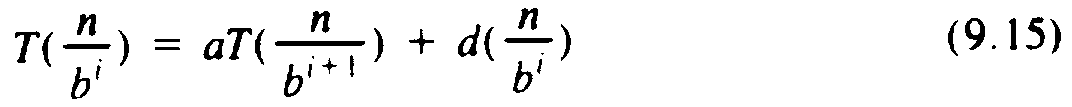
Thus, starting with (9.14) and substituting (9.15) for i = 1, 2, . . . , we get
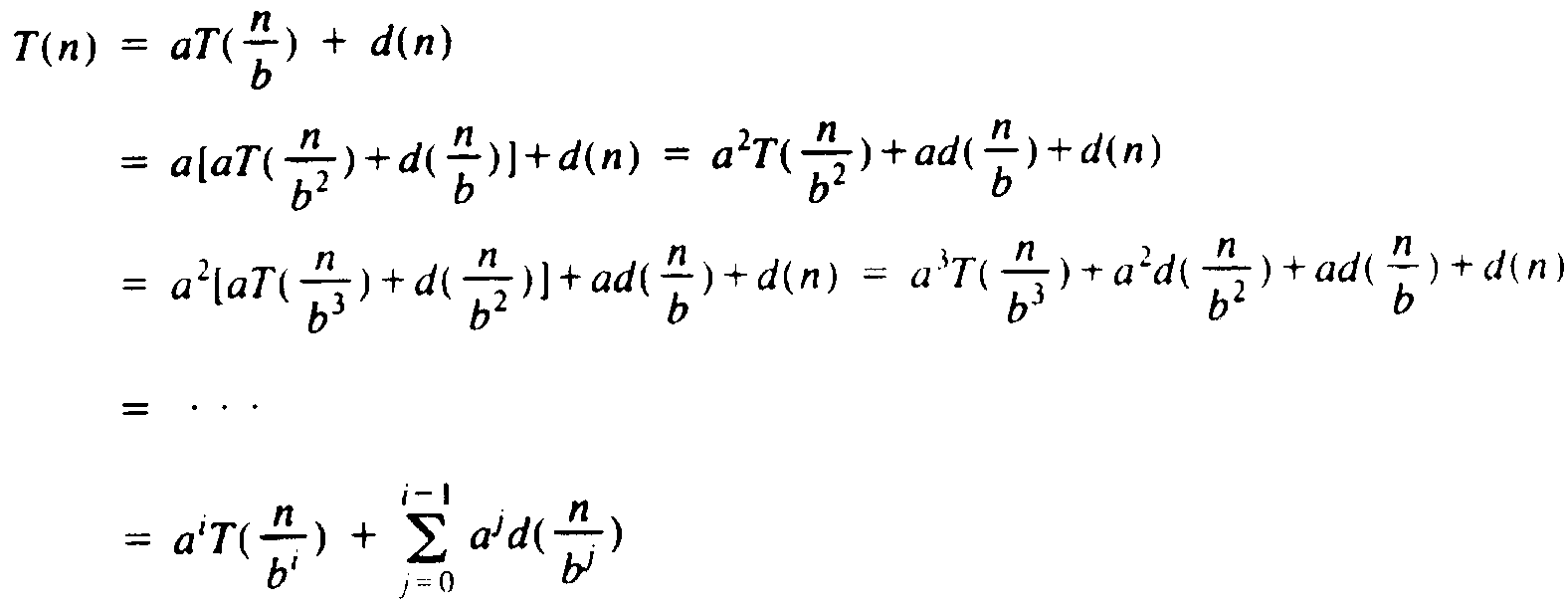
Now, if we assume n = bk, we can use the fact that T(n/bk) = T(1) = 1 to get from the above, with i = k, the formula
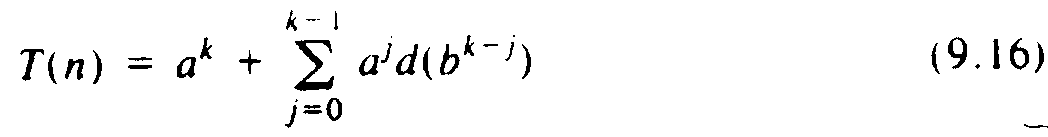
If we use the fact that k = logbn, the first term of (9.16) can be written as alogbn , or equivalently nlogba (take logarithms to the base b of both expressions to see that they are the same). This expression is n to a constant power. For example, in the case of mergesort, where a = b = 2, the first term is n. In general, the larger a is, i.e., the more subproblems we need to solve, the higher the exponent will be; the higher b is, i.e., the smaller each subproblem is, the lower will be the exponent.
It is interesting to see the different roles played by the two terms in (9.16). The first, ak or nlogba, is called the homogeneous solution, in analogy with differential equation terminology. The homogeneous solution is the exact solution when d(n), called the driving function, is 0 for all n. In other words, the homogeneous solution represents the cost of solving all the subproblems, even if subproblems can be combined "for free."
On the other hand, the second term of (9.16) represents the cost of creating the subproblems and combining their results. We call this term the particular solution. The particular solution is affected by both the driving function and the number and size of subproblems. As a rule of thumb if the homogeneous solution is greater than the driving function, then the particular solution has the same growth rate as the homogeneous solution. If the driving function grows faster than the homogeneous solution by more than nÎ for some Î > 0, then the particular solution has the same growth rate as the driving function. If the driving function has the same growth rate as the homogeneous solution, or grows faster by at most logkn for some k, then the particular solution grows as logn times the driving function.
It is important to recognize that when searching for improvements in an algorithm, we must be alert to whether the homogeneous solution is larger than the driving function. For example, if the homogeneous solution is larger, then finding a faster way to combine subproblems will have essentially no effect on the efficiency of the overall algorithm. What we must do in that case is find a way to divide a problem into fewer or smaller subproblems. That will affect the homogeneous solution and lower the overall running time.
If the driving function exceeds the homogeneous solution, then one must try to decrease the driving function. For example, in the mergesort case, where a = b = 2, and d(n) = cn, we shall see that the particular solution is O(nlogn). However, reducing d(n) to a slightly sublinear function, say n0.9, will, as we shall see, make the particular solution less than linear as well and reduce the overall running time to O(n), which is the homogeneous solution. †
Example 9.2. The multiplicative functions that are of greatest interest to us are of the form na for any positive a. To prove f(n) = na is multiplicative, we have only to observe that (xy)a = xaya.
Now if d(n) in (9.16) is multiplicative, then d(bk-j) = (d(b))k-j, and the particular solution of (9.16) is
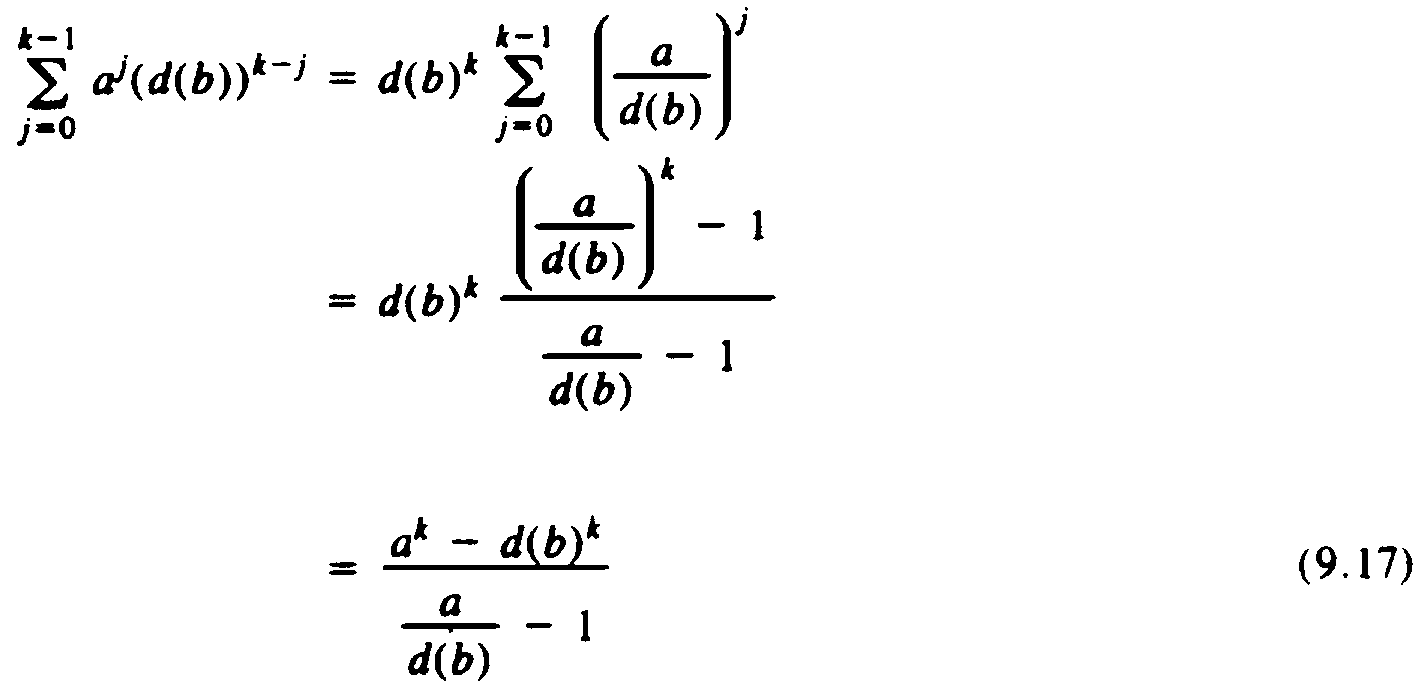
There are three cases to consider, depending on whether a is greater than, less than, or equal to d(b).
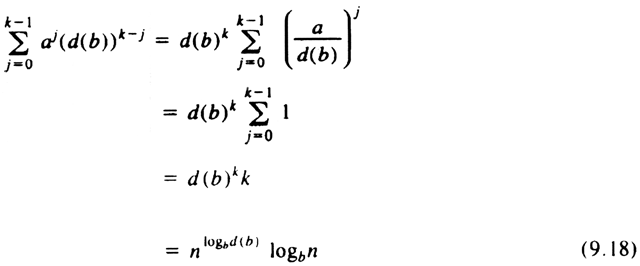
Since a = d(b), the particular solution given by (9.18) is logbn times the homogeneous solution, and again the particular solution exceeds the homogeneous. In the special case d(n) = na, (9.18) reduces to O(nalogn), by observations similar to those in Case (2).
Example 9.3. Consider the following recurrences, with T(1) = 1.
In each case, a = 4, b = 2, and the homogeneous solution is n2. In Equation (1), with d(n) = n, we have d(b) = 2. Since a = 4 > d(b), the particular solution is also n2, and T(n) is O(n2) in (1).
In Equation (3), d(n) = n3 d(b) = 8, and a < d(b). Thus the particular solution is O(nlogbd(b)) = O(n3), and T(n) of Equation (3) is O(n3). We can deduce that the particular solution is of the same order as d(n) = n3, using the observations made above about d(n)'s of the form na in analyzing the case a < d(b) of (9.17). In Equation (2) we have d(b) = 4 = a, so (9.18) applies. As d(n) is of the form na, the particular solution, and therefore T(n) itself, is O(n2 log n).
These are other functions that are not multiplicative, yet for which we can get solutions for (9.16) or even (9.17). We shall consider two examples. The first generalizes to any function that is the product of a multiplicative function and a constant greater than or equal to one. The second is typical of a case where we must examine (9.16) in detail and get a close upper bound on the particular solution.
Example 9.4. Consider
T(1) = 1 T(n) = 3T(n/2) + 2n1.5
Now 2n1.5 is not multiplicative, but n1.5 is. Let U(n) = T(n)/2 for all n. Then
U(1) = 1/2 U(n) = 3U(n/2) + n1.5
The homogeneous solution, if U(1) were 1, would be nlog 3 < n1.59; since U(1) = 1/2 we can easily show the homogeneous solution is less than n1.59/2; certainly it is O(n1.59). For the particular solution, we can ignore the fact that U(1) ¹ 1, since increasing U(1) will surely not lower the particular solution. Then since a = 3, b = 2, and b1.5 = 2.83 < a, the particular solution is also O(n1.59), and that is the growth rate of U(n). Since T(n) = 2U(n), T(n) is also O(n1.59) or O(nlog 3).
Example 9.5. Consider
T(1) = 1 T(n) = 2T(n/2) + n log n
The homogeneous solution is easily seen to be n, since a = b = 2. However, d(n) = n log n is not multiplicative, and we must sum the particular solution formula in (9.16) by ad hoc means. That is, we want to evaluate
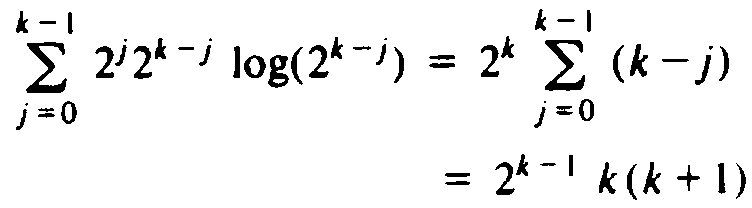
Since k = log n we have the particular solution O (n log2n), and this solution, being greater than the homogeneous, is also the value of T(n) that we obtain.
Exercises
| 9.1 | Write recurrence equations for the time and space complexity of the
following algorithm, assuming n is a power of 2.
function path ( s, t, n: integer ) : boolean;
begin
if n = 1 then
if edge (s, t) then
return (true)
else
return (false);
{ if we reach here, n > 1 }
for i := 1 to n do
if path(s, i, n div 2) and
path (i, t, n div 2) then
return (true);
return (false)
end; { path }
The function edge(i, j) returns true if vertices i and j of an n-vertex graph are connected by an edge or if i = j; edge(i, j) returns false otherwise. What does the program do? |
|---|---|
| 9.2 | Solve the following recurrences, where T(1) = 1 and T(n) for n
³ 2
satisfies:
|
| 9.3 | Solve the following recurrences, where T(1) = 1 and T(n) for n
³ 2
satisfies:
|
| 9.4 | Give tight big-oh and big-omega bounds on T(n) defined by the
following recurrences. Assume T(1) = 1.
|
| *9.5 | Solve the following recurrences by guessing a solution and checking
your answer.
|
| 9.6 | Check your answers to Exercise 9.5 by solving the recurrences by repeated substitution. |
| 9.7 | Generalize Exercise 9.6 by solving all recurrences of the form
T(1) = 1
T(n) = aT(n-1) + d(n) for n ³ 1
in terms of a and d(n). |
| *9.8 | Suppose in Exercise 9.7 that d(n) = cn for some constant c ³ 1. How does the solution to T(n) depend on the relationship between a and c. What is T(n)? |
| **9.9 | Solve for T(n):
T(1) = 1
T(n) = Ö`nT(Ö`n) + n for n ³ 2
|
| 9.10 | Find closed form expressions for the following sums.
|
| *9.11 | Show that the number of different orders in which to multiply a
sequence of n matrices is given by the recurrence
Show that
|
| **9.12 | Show that the number of comparisons required to sort n elements
using mergesort is given by
T(1) = 0 T(n) = T([n/2]) + T([n/2]) + n - 1 where [x] denotes the integer part of x and [x] denotes the smallest integer ³ x. Show that the solution to this recurrence is T(n) = n[logn] - 2[logn] + 1 |
| 9.13 | Show that the number of Boolean functions of n variables is given by
the recurrence
T(1) = 4 T(n) = (T(n - 1))2 Solve for T(n). |
| **9.14 | Show that the number of binary trees of height £ n is
given by the
recurrence
T(1) = 1 T(n) = (T(n - 1))2 + 1 Show that T(n) = [k2n] for some constant k. What is the value of k? |
Bentley, Haken, and Saxe [1978], Greene and Knuth [1983], Liu [1968], and Lueker [1980] contain additional material on the solution of recurrences. Aho and Sloane [1973] show that many nonlinear recurrences of the form T(n) = (T(n-1))2 + g(n) have a solution of the form T(n) = [k2n] where k is a constant, as in Exercise 9.14.
† But don't hold out much hope for discovering a way to merge two sorted lists of n/2 elements in less than linear time; we couldn't even look at all the elements on the list in that case.