Slide 6.6: Denotational semantics of integer arithmetic expressions
Home

|
Slide 6.4: Semantic functions Slide 6.6: Denotational semantics of integer arithmetic expressions Home |

|
N: Number → Integer
N ::= N D | D
and is given by the following equations:
N[[ND]]= 10 * N[[N]] + N[[D]] N[[D]] = D[[D]]Here
[[ND]] refers to the tree node  and
and [[D]] to the node 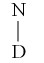 .
.
N[['65']] = 10 * N[['6']] + D[['5']] = 10 * D[['6']] + 5 = 10 * 6 + 5 = 60 + 5 = 65
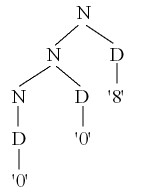
Solely using the specification of the semantics of numerals, N[['008']] = N[['8']] can also be proved as follows:
N[['008']] = 10*N[['00']]+D[['8']] = 10*( 10*N[['0']]+D[['0']] )+8 = 10*( 10*D[['0']]+0 )+8 = 10*( 10*0+0 )+8 = 8 = D[['8']] = N[['8']] |
|
<N> ⇒ <N> <D> ⇒ <N> <D> <D> ⇒ <D> <D> <D> ⇒ '0' <D> <D> ⇒ '00' <D> ⇒ '008'