<sentence> ::= abc | a<thing>bc
<thing>b ::= b<thing>
<thing>c ::= <other>bcc
a<other> ::= aa | aa<thing>
b<other> ::= <other>b
derive the <sentence> aaabbbcccAns>
<sentence> ⇒ a<thing>bc
⇒ ab<thing>c
⇒ ab<other>bcc
⇒ a<other>bbcc
⇒ aa<thing>bbcc
⇒ aab<thing>bcc
⇒ aabb<thing>cc
⇒ aabb<other>bccc
⇒ aab<other>bbccc
⇒ aa<other>bbbccc
⇒ aaabbbccc
a, b} defined by the following grammar: (20%)
<string> ::= a <B> | b <A>
<A> ::= a | a <string> | b <A> <A>
<B> ::= b | b <string> | b <B> <B>
Ans>
-
This grammar generates a language, which is too complicated to be described easily.
However, the following grammar generates a language, in which all strings have equal numbers of
a's and b's.
<string> ::= a <B> | b <A> <A> ::= a | a <string> | b <A> <A> <B> ::= b | b <string> | a <B> <B>
<stmt> ::= if <expr> then <stmt> | <matchedStmt>
<matchedStmt> ::= if <expr> then <matchedStmt> else <stmt> | other
<expr> ::= 0 | 1
Ans>
-
The solutions use the following grammar, which is slightly different from the above grammar.
<statement> ::= if ( <exp> ) <statement> | <matched-stmt>
<matched-stmt> ::= if ( <exp> ) <matched-stmt> else <statement> | other
<exp> ::= 0 | 1
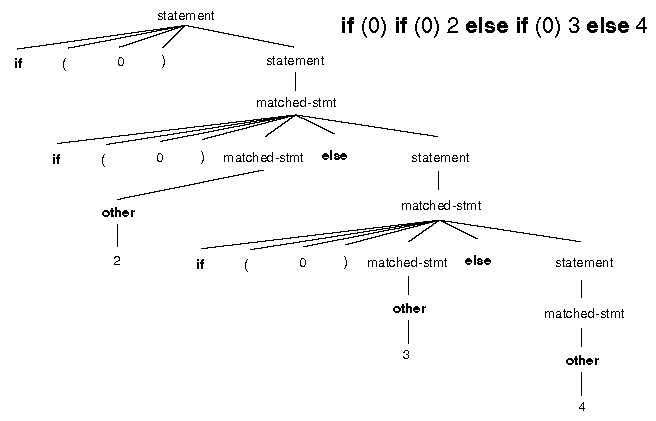
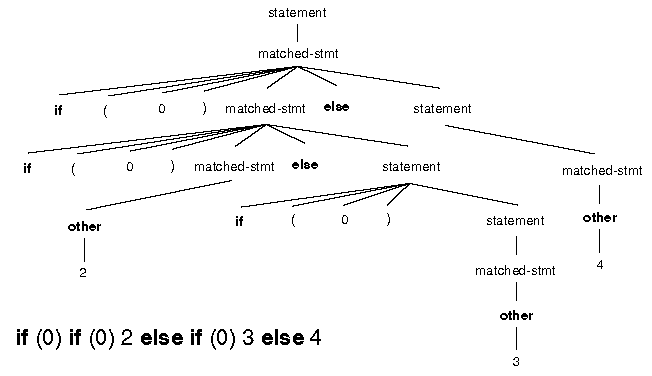
Ans>
<roman> ::= <tens> <units> <tens> ::= <low tens> | XL | L <low tens> | XC <low tens> ::= ε | X | XX | XXX <units> ::= <low units> | IV | V <low units> | IX <low units> ::= ε | I | II | III