What Is Backpropagation? (Cont.)

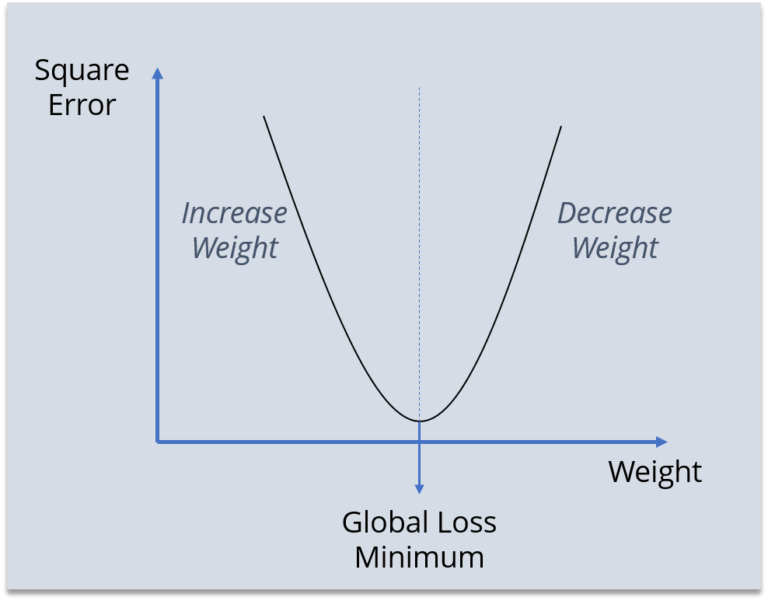
Now, what we did here:
  1. We first initialized some random value to ‘W’ and propagated forward.
  2. Then, we noticed that there is some error. To reduce that error, we propagated backwards and increased the value of ‘W’.
  3. After that, also we noticed that the error has increased. We came to know that, we can’t increase the ‘W’ value.
  4. So, we again propagated backwards and we decreased ‘W’ value.
  5. Now, we noticed that the error has reduced.
It is a strategy that is called “gradient descent,” which is simply used to find the values of a function’s parameters (coefficients) that minimize a cost function as far as possible. You start by defining the initial parameter’s values and from there gradient descent uses calculus to iteratively adjust the values so they minimize the given cost-function.
So, we are trying to get the value of weight such that the error becomes minimum. Basically, we need to figure out whether we need to increase or decrease the weight value.

Once we know that, we keep on updating the weight value in that direction until error becomes minimum. You might reach a point, where if you further update the weight, the error will increase. At that time you need to stop, and that is your final weight value as shown in the figure.

That is we need to reach the “Global Loss Minimum,” and it is the purpose of backpropagation.

Review: Backpropagation Neural Netowrks
    Which statement is NOT true about backpropagation neural networks?

      It uses a supervised learning algorithm.
      The gradient descent strategy is used by backpropagation.
      The multi-layer perceptron is one of backpropagation networks.
      The purpose of backpropagation is to reach the global loss minimum.
Result: