There are two ways to create a primary key automatically: (i)
IDENTITY columns and (ii) creating a SEQUENCE.
IDENTITY Columns
IDENTITY columns were introduced in Oracle 12c, allowing for simple auto increment functionality in modern versions of Oracle.
This new feature makes sequences obsolete and alleviates the need to specify a sequencename.nextval clause in insert SQL.
In a nutshell, the identity columns will replace Oracle sequences as a method for identifying unique table rows for a primary key.
There are several types of identity columns:
GENERATED ALWAYS AS IDENTITY (the same as GENERATED AS ALWAYS)GENERATED BY DEFAULT AS IDENTITYGENERATED BY DEFAULT ON NULL AS IDENTITYGENERATED ALWAYS AS IDENTITY
DEFAULTclause: Value is generated from an identity sequence, andNULL: Allows the identity to be used if the identity column is referenced, but a value ofNULLis specified.
SQL> DROP TABLE course3;
Table dropped.
SQL> CREATE TABLE course3 (
2 cnumber NUMBER GENERATED BY DEFAULT ON NULL AS IDENTITY,
3 title VARCHAR2(64) NOT NULL );
Table created.
SQL> INSERT INTO course3( title ) VALUES ( 'Databases' );
1 row created.
SQL> INSERT INTO course3( title ) VALUES ( 'Advanced Database Systems' );
1 row created.
SQL> INSERT INTO course3( title ) VALUES ( 'Data Engineering and Mining' );
1 row created.
SQL> SELECT * FROM course3;
CNUMBER TITLE
---------- ------------------------------------
1 Databases
2 Advanced Database Systems
3 Data Engineering and Mining
|
Demonstration
Below is an SQL test area from W3Schools, which uses the well-known Northwind sample database. The tables here are for read only because of the problem of embedding the scripts. For a fully working example, check this by using Chrome.
|
Result:
|
The Database includes:
|
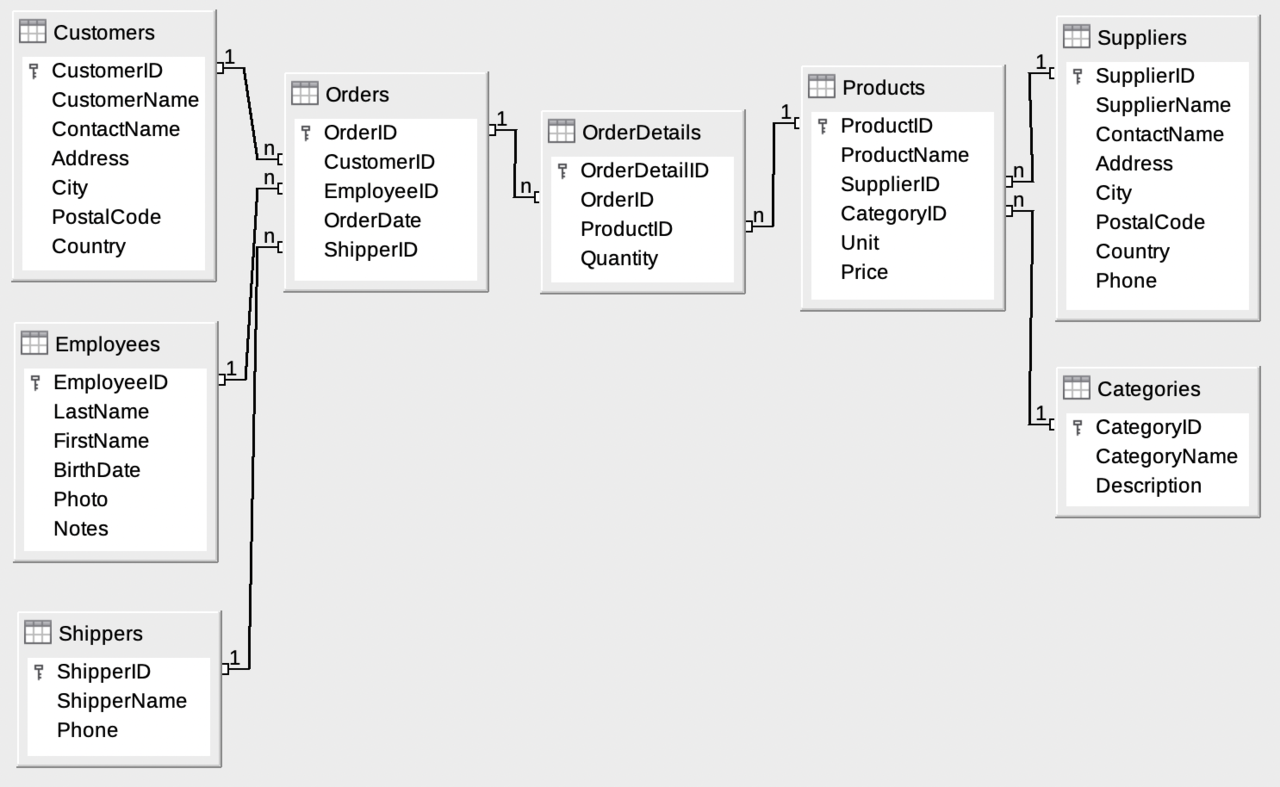
|
The Database includes:
|