The PageRank algorithm assigns a PageRank score to each webpage. The PageRank score of a webpage represents the probability that a random web surfer chooses to view the webpage.
Directed Web Graph
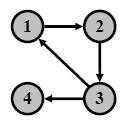
The PageRank represents the Web’s link structure as a directed graph.
| Webpages are nodes of the graph, and links from webpages to other webpages are edges that show direction of movement. To faciltate the discussion, the PageRank algorithm is applied to the directed graph on the right. |
|
Web Hyperlink Matrix
The process for determining PageRank begins by expressing the directed web graph as the
n×n “hyperlink matrix” H, where n is the number of webpages.
If webpage i has li≥1 links to other webpages and webpage i links to webpage j, then the element in row i and column j of H is Hij=1/li.
Otherwise, Hij=0.
Thus, Hij represents the likelihood that a random surfer selects a link from webpage i to webpage j.
For the directed graph in the above figure, the H is given on the right.
Node 4 is a dangling node because it does not link to other nodes.
As a result, all entries in row 4 of the example matrix are zero.
|
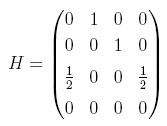
|
This means the probability is zero that a random surfer moves from node 4 to any other node in the directed graph. The majority of webpages are dangling nodes (e.g., postscript files and image files), so there are many rows with all zero entries in the web hyperlink matrix. When a web surfer lands on dangling node webpages, the surfer can either stop surfing or move to another webpage, perhaps by entering the Uniform Resource Locator (URL) of a different webpage in the address line of a web browser.
|
“I have lived with several Zen masters — all of them cats.” ― Eckhart Tolle, The Power of Now: A Guide to Spiritual Enlightenment |