|


|
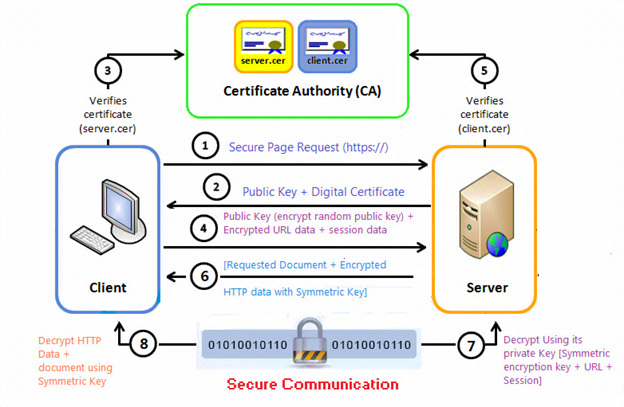
- Public key + encrypted URL data + session data, where a session key is an encryption and decryption key that is generated to ensure the security of a communications session between two computers.
- Certificate verification (client.cer), where client certificates (client.cer) are used to identify a client to a respective user, which means authenticating the client to the server.
- (Step 7 in the diagram) Decrypt using its private key (symmetric encryption key + URL + session), where the web server decrypts the symmetric encryption key using its private key and uses the symmetric key to decrypt the URL and HTTP data.
- (Step 6 in the diagram) (Requested document + encrypted HTTP data with symmetric key), where the web server sends back the requested HTML document and HTTP data encrypted with the symmetric key.
- Decrypt HTTP data + document using symmetric key, where the browser decrypts the HTTP data and HTML document using the symmetric key and displays the information.
|
According to most studies, people’s number one fear is public speaking. Number two is death. Death is number two. Does that sound right? This means to the average person, if you go to a funeral, you’re better off in the casket than doing the eulogy. — Jerry Seinfeld |