Computer hardware simulates how human perform addition. For addition, digits are added bit by bit from right to left, with carries passed to the next digit to the left. For example,
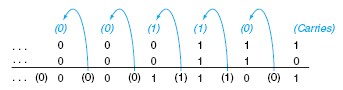
0000 0000 0000 0000 0000 0000 0000 01112 = 710 + 0000 0000 0000 0000 0000 0000 0000 01102 = 610 ——————————————————————————————————————————————— = 0000 0000 0000 0000 0000 0000 0000 11012 = 1310The 4 bits to the right have all the action; the figure shows the sums and carries of the 6 bits. The carries are shown in parentheses, with the arrows showing how they are passed.
| The rightmost bit adds 1 to 0, resulting in the sum of this bit being 1 and the carry out from this bit being 0. |
|
Hence, the operation for the second digit to the right is 0 + 1 + 1. This generates a 0 for this sum bit and a carry out of 1. The third digit is the sum of 1 + 1 + 1, resulting in a carry out of 1 and a sum bit of 1. The fourth bit is 1 + 0 + 0, yielding a 1 sum and no carry. On the other hand, the subtraction is shown next:
0000 0000 0000 0000 0000 0000 0000 01112 = 710 – 0000 0000 0000 0000 0000 0000 0000 01102 = 610 ——————————————————————————————————————————————— = 0000 0000 0000 0000 0000 0000 0000 00012 = 110Instead of using subtraction hardware, the subtraction uses addition hardware: the appropriate operand is simply negated (two’s complemented) before being added.
0000 0000 0000 0000 0000 0000 0000 01112 = 710 + 1111 1111 1111 1111 1111 1111 1111 10102 = -610 ——————————————————————————————————————————————— = 0000 0000 0000 0000 0000 0000 0000 00012 = 110
|
“Where wisdom reigns, there is no conflict between thinking and feeling.” ― Carl Gustav Jung |