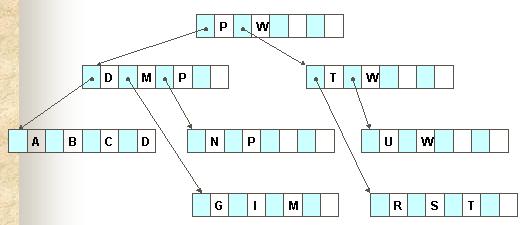
| For example, the figure on the right shows an example of a B-tree defined in the textbook. |
|
A balanced search tree in which every node has between ⌈m/2⌉ and m children, where m>1 is an integer. Root may have as few as zero child and leaves have no children.The maximum number of keys in a record is called the order of the B-tree. Not all the keys of a B-tree are stored in the leaves. Thus, the B-trees discussed in the textbook are actually B+ trees without sequential links. We will follow the terminology used in the textbook. A B+ tree is
A B-tree where the leaves are linked sequentially, thus allowing both fast random access and sequential access to data. The keys of a B+ tree are stored in the leaves.
| For example, the figure on the right shows an example of a B-tree defined in the textbook. |

|