A Binary Search Tree (Cont.)

---

Insertion and Deletion
The running time of an insertion and deletion on a binary search tree is O(h), where h is the height of the tree. This performance is good compared to the one of a simple index which involves moving a large number of the other keys for an insertion or deletion. Thus, a binary search tree solves the second problem but not the first problem.

Implementation

The figure on the right repeats the figure in the previous slide.

The following figure shows an implementation of the above binary search tree with a key LV added.

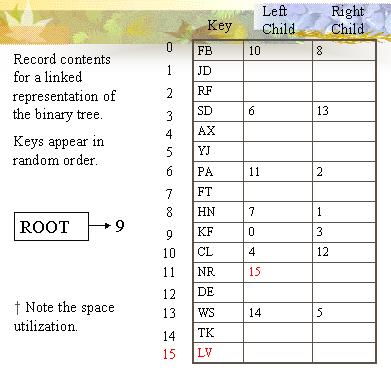
Each node is treated as a fixed-length record in which the link fields contain relative record numbers (RRNs) pointing to other nodes, then it is possible to place such a tree structure on secondary storage. The records appear in random rather than sorted order. All the information about the logical structure is carried in the link fields.