In a public-key cryptosystem, each participant has both a public key and a secret key. Each key is a piece of information. For example, in the RSA cryptosystem, each key consists of a pair of integers. The participants "Alice" and "Bob" are traditionally used in cryptography examples; we denote their public and secret keys as PA, SA for Alice and PB, SB for Bob.
Each participant creates his own public and secret keys. Each keeps his secret key secret, but he can reveal his public key to anyone or even publish it. In fact, it is often convenient to assume that everyone's public key is available in a public directory, so that any participant can easily obtain the public key of any other participant.
The public and secret keys specify functions that can be applied to any message. Let 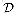 denote the set of permissible messages. For example,
denote the set of permissible messages. For example, 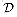 might be the set of all finite-length bit sequences. We require that the public and secret keys specify one-to-one functions from
might be the set of all finite-length bit sequences. We require that the public and secret keys specify one-to-one functions from 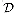 to itself. The function corresponding to Alice's public key P
to itself. The function corresponding to Alice's public key P
 b (mod n) by using Euclid's algorithm. The Chinese remainder theorem is presented in Section 33.5. Section 33.6 considers powers of a given number a, modulo n, and presents a repeated-squaring algorithm for efficiently computing ab mod n, given a, b, and n. This operation is at the heart of efficient primality testing. Section 33.7 then describes the RSA public-key cryptosystem. Section 33.8 describes a randomized primality test that can be used to find large primes efficiently, an essential task in creating keys for the RSA cryptosystem. Finally, Section 33.9 reviews a simple but effective heuristic for factoring small integers. It is a curious fact that factoring is one problem people may wish to be intractable, since the security of RSA depends on the difficulty of factoring large integers.
b (mod n) by using Euclid's algorithm. The Chinese remainder theorem is presented in Section 33.5. Section 33.6 considers powers of a given number a, modulo n, and presents a repeated-squaring algorithm for efficiently computing ab mod n, given a, b, and n. This operation is at the heart of efficient primality testing. Section 33.7 then describes the RSA public-key cryptosystem. Section 33.8 describes a randomized primality test that can be used to find large primes efficiently, an essential task in creating keys for the RSA cryptosystem. Finally, Section 33.9 reviews a simple but effective heuristic for factoring small integers. It is a curious fact that factoring is one problem people may wish to be intractable, since the security of RSA depends on the difficulty of factoring large integers.


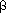 -bit integers by the ordinary method uses
-bit integers by the ordinary method uses  (
( |a|. If d | a, then we also say that a is a multiple of d. If d does not divide a, we write
|a|. If d | a, then we also say that a is a multiple of d. If d does not divide a, we write 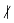 .
. 0, we say that d is a divisor of a. Note that d | a if and only if -d | a, so that no generality is lost by defining the divisors to be nonnegative, with the understanding that the negative of any divisor of a also divides a. A divisor of an integer a is at least 1 but not greater than |a|. For example, the divisors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.
0, we say that d is a divisor of a. Note that d | a if and only if -d | a, so that no generality is lost by defining the divisors to be nonnegative, with the understanding that the negative of any divisor of a also divides a. A divisor of an integer a is at least 1 but not greater than |a|. For example, the divisors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.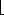 a/n
a/n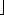 is the quotient of the division. The value r = a mod n is the remainder (or residue) of the division. We have that n | a if and only if a mod n = 0. It follows that
is the quotient of the division. The value r = a mod n is the remainder (or residue) of the division. We have that n | a if and only if a mod n = 0. It follows that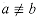 b (mod n) if a is not equivalent to b, modulo n. For example, 61
b (mod n) if a is not equivalent to b, modulo n. For example, 61  Z} .
Z} . b.
b. j, we have gcd(ni, nj) = 1.
j, we have gcd(ni, nj) = 1.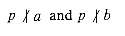 . Thus, gcd(a, p) = 1 and gcd(b, p) = 1, since the only divisors of p are 1 and p, and by assumption p divides neither a nor b. Theorem 33.6 then implies that gcd(ab, p) = 1, contradicting our assumption that p | ab, since p | ab implies gcd(ab, p) = p. This contradiction completes the proof.
. Thus, gcd(a, p) = 1 and gcd(b, p) = 1, since the only divisors of p are 1 and p, and by assumption p divides neither a nor b. Theorem 33.6 then implies that gcd(ab, p) = 1, contradicting our assumption that p | ab, since p | ab implies gcd(ab, p) = p. This contradiction completes the proof. 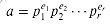
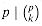 . Conclude that for all integers a, b, and primes p,
. Conclude that for all integers a, b, and primes p,
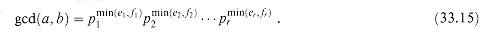
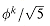 , where
, where  is the golden ratio
is the golden ratio 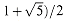 defined by equation (2.14), the number of recursive calls in EUCLID is O(lg b). (See Exercise 33.2-5 for a tighter bound.) It follows that if EUCLID is applied to two
defined by equation (2.14), the number of recursive calls in EUCLID is O(lg b). (See Exercise 33.2-5 for a tighter bound.) It follows that if EUCLID is applied to two  14.
14. EXTENDED-EUCLID(b, a mod b)
EXTENDED-EUCLID(b, a mod b) lg k
lg k pairs of numbers derived from the ni are relatively prime.
pairs of numbers derived from the ni are relatively prime.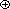 ) is a set S together with a binary operation
) is a set S together with a binary operation 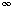 , then it is a finite group.
, then it is a finite group.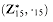
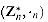 . The elements of this group are the set
. The elements of this group are the set 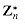 of elements in Zn that are relatively prime to n:
of elements in Zn that are relatively prime to n: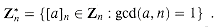
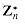 is well defined, note that for 0
is well defined, note that for 0 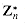 is well defined. An example of such a group is
is well defined. An example of such a group is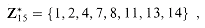
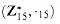 . For example, 8
. For example, 8  11
11 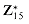 . The identity for this group is 1.
. The identity for this group is 1.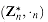 is a finite abelian group.
is a finite abelian group.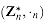 is closed. Associativity and commutativity can be proved for .n as they were for +n in the proof of Theorem 33.12. The identity element is [1]n. To show the existence of inverses, let a be an element of
is closed. Associativity and commutativity can be proved for .n as they were for +n in the proof of Theorem 33.12. The identity element is [1]n. To show the existence of inverses, let a be an element of 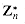 and let (d, x, y) be the output of EXTENDED-EUCLID(a, n). Then d = 1, since a
and let (d, x, y) be the output of EXTENDED-EUCLID(a, n). Then d = 1, since a 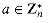 , and
, and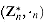 as Zn and
as Zn and 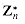 respectively.
respectively.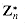 is defined by the equation a/b
is defined by the equation a/b 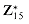 we have that 7-1
we have that 7-1 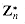 is denoted
is denoted 
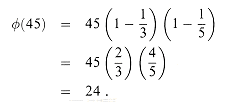
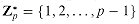 , and
, and S, and (S',
S, and (S', 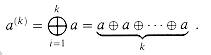
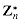 , we have a(k) = ak mod n. The subgroup generated by a, denoted
, we have a(k) = ak mod n. The subgroup generated by a, denoted  a
a or (
or (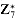 , we have
, we have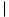
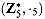 . Show that these groups are isomorphic by exhibiting a one-to-one correspondence
. Show that these groups are isomorphic by exhibiting a one-to-one correspondence  between their elements such that a + b
between their elements such that a + b 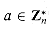 , the function fa:
, the function fa: 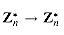 defined by fa(x) = ax mod n is a permutation of
defined by fa(x) = ax mod n is a permutation of 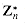 .
.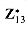 .
.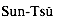 solved the problem of finding those integers x that leave remainders 2, 3, and 2 when divided by 3, 5, and 7 respectively. One such solution is x = 23; all solutions are of the form 23 + 105k for arbitrary integers k. The "Chinese remainder theorem" provides a correspondence between a system of equations modulo a set of pairwise relatively prime moduli (for example, 3, 5, and 7) and an equation modulo their product (for example, 105).
solved the problem of finding those integers x that leave remainders 2, 3, and 2 when divided by 3, 5, and 7 respectively. One such solution is x = 23; all solutions are of the form 23 + 105k for arbitrary integers k. The "Chinese remainder theorem" provides a correspondence between a system of equations modulo a set of pairwise relatively prime moduli (for example, 3, 5, and 7) and an equation modulo their product (for example, 105). (al, a2, . . . , ak),
(al, a2, . . . , ak),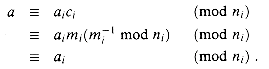
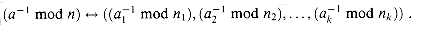
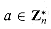 :
: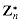 generated by a, and let ordn (a) (the "order of a, modulo n") denote the order of a in
generated by a, and let ordn (a) (the "order of a, modulo n") denote the order of a in 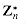 . For example,
. For example, 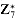 , and ord7 (2) = 3. Using the definition of the Euler phi function
, and ord7 (2) = 3. Using the definition of the Euler phi function 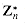 (see Section 33.3), we now translate Corollary 33.19 into the notation of
(see Section 33.3), we now translate Corollary 33.19 into the notation of 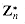 to obtain Euler's theorem and specialize it to
to obtain Euler's theorem and specialize it to 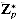 , where p is prime, to obtain Fermat's theorem.
, where p is prime, to obtain Fermat's theorem.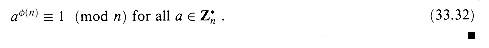

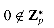 . For all a
. For all a 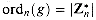 , then every element in
, then every element in 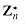 is a power of g, modulo n, and we say that g is a primitive root or a generator of
is a power of g, modulo n, and we say that g is a primitive root or a generator of 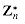 . For example, 3 is a primitive root, modulo 7. If
. For example, 3 is a primitive root, modulo 7. If 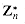 possesses a primitive root, we say that the group
possesses a primitive root, we say that the group 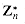 is cyclic. We omit the proof of the following theorem, which is proven by Niven and Zuckerman [151].
is cyclic. We omit the proof of the following theorem, which is proven by Niven and Zuckerman [151].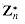 is cyclic are 2, 4, pe, and 2pe, for all odd primes p and all positive integers e.
is cyclic are 2, 4, pe, and 2pe, for all odd primes p and all positive integers e. 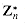 and a is any element of
and a is any element of 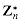 , then there exists a z such that gz
, then there exists a z such that gz 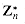 , then the equation gx
, then the equation gx 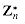 has a primitive root g. Equation (33.34) can be written
has a primitive root g. Equation (33.34) can be written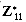 . Pick the smallest primitive root g and compute a table giving ind11,g (x) for all x
. Pick the smallest primitive root g and compute a table giving ind11,g (x) for all x 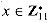 .
.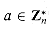 using the procedure MODULAR-EXPONENTIATION, assuming that you know
using the procedure MODULAR-EXPONENTIATION, assuming that you know 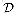 denote the set of permissible messages. For example,
denote the set of permissible messages. For example, 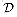 might be the set of all finite-length bit sequences. We require that the public and secret keys specify one-to-one functions from
might be the set of all finite-length bit sequences. We require that the public and secret keys specify one-to-one functions from 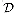 to itself. The function corresponding to Alice's public key P
to itself. The function corresponding to Alice's public key P