The first three sections of this chapter cover the three most common techniques used in amortized analysis. Section 18.1 starts with the aggregate method, in which we determine an upper bound T(n) on the total cost of a sequence of n operations. The amortized cost per operation is then T(n)/n.
Section 18.2 covers the accounting method, in which we determine an amortized cost of each operation. When there is more than one type of operation, each type of operation may have a different amortized cost. The accounting method overcharges some operations early in the sequence, storing the overcharge as "prepaid credit" on specific objects in the data structure. The credit is used later in the sequence to pay for operations that are charged less than they actually cost.
Section 18.3 discusses the potential method, which is like the accounting method in that we determine the amortized cost of each operation and may overcharge operations early on to compensate for undercharges later. The potential method maintains the credit as the "potential energy" of the data structure instead of associating the credit with individual objects within the data structure.
We shall use two examples to examine these three models. One is a stack with the additional operation MULTIPOP, which pops several objects at once. The other is a binary counter that counts up from 0 by means of the single operation INCREMENT.
While reading this chapter, bear in mind that the charges assigned during an amortized analysis are for analysis purposes only. They should not appear in the code. If, for example, a credit is assigned to an object x when using the accounting method, there is no need to assign an appropriate amount to some attribute credit[x] in the code.
The insight into a particular data structure gained by performing an amortized analysis can help in optimizing the design. In Section 18.4, for example, we shall use the potential method to analyze a dynamically expanding and contracting table.
18.1 The aggregate method
In the aggregate method of amortized analysis, we show that for all n, a sequence of n operations takes worst-case time T(n) in total. In the worst case, the average cost, or amortized cost, per operation is therefore T(n) / n. Note that this amortized cost applies to each operation, even when there are several types of operations in the sequence. The other two methods we shall study in this chapter, the accounting method and the potential method, may assign different amortized costs to different types of operations.
In our first example of the aggregate method, we analyze stacks that have been augmented with a new operation. Section 11.1 presented the two fundamental stack operations, each of which takes O(1) time:
PUSH(S, x) pushes object x onto stack S.
POP(S) pops the top of stack S and returns the popped object.
Since each of these operations runs in O(1) time, let us consider the cost of each to be 1. The total cost of a sequence of n PUSH and POP operations is therefore n, and the actual running time for n operations is therefore
The situation becomes more interesting if we add the stack operation MULTIPOP(S, k), which removes the k top objects of stack S, or pops the entire stack if it contains less than k objects. In the following pseudocode, the operation STACK-EMPTY returns TRUE if there are no objects currently on the stack, and FALSE otherwise.
Figure 18.1 shows an example of MULTIPOP.
What is the running time of MULTIPOP(S, k) on a stack of s objects? The actual running time is linear in the number of POP operations actually executed, and thus it suffices to analyze MULTIPOP in terms of the abstract costs of 1 each for PUSH and POP. The number of iterations of the while loop is the number min(s, k) of objects popped off the stack. For each iteration of the loop, one call is made to POP in line 2. Thus, the total cost of MULTIPOP is min(s, k), and the actual running time is a linear function of this cost.
Let us analyze a sequence of n PUSH, POP, and MULTIPOP operations on an initially empty stack. The worst-case cost of a MULTIPOP operation in the sequence is O(n), since the stack size is at most n. The worst-case time of any stack operation is therefore O(n), and hence a sequence of n operations costs O(n2), since we may have O(n) MULTIPOP operations costing O(n) each. Although this analysis is correct, the O(n2) result, obtained by considering the worst-case cost of each operation individually, is not tight.
Using the aggregate method of amortized analysis, we can obtain a better upper bound that considers the entire sequence of n operations. In fact, although a single MULTIPOP operation can be expensive, any sequence of n PUSH, POP, and MULTIPOP operations on an initially empty stack can cost at most O(n). Why? Each object can be popped at most once for each time it is pushed. Therefore, the number of times that POP can be called on a nonempty stack, including calls within MULTIPOP, is at most the number of PUSH operations, which is at most n. For any value of n, any sequence of n PUSH, POP, and MULTIPOP operations takes a total of O(n) time. The amortized cost of an operation is the average: O(n)/n = O(1).
We emphasize again that although we have just shown that the average cost, and hence running time, of a stack operation is O(1), no probabilistic reasoning was involved. We actually showed a worst-case bound of O(n) on a sequence of n operations. Dividing this total cost by n yielded the average cost per operation, or the amortized cost.
As another example of the aggregate method, consider the problem of implementing a k-bit binary counter that counts upward from 0. We use an array A[0 . . k - 1] of bits, where length[A] = k, as the counter. A binary number x that is stored in the counter has its lowest-order bit in A[0] and its highest-order bit in A[k - 1], so that
This algorithm is essentially the same one implemented in hardware by a ripple-carry counter (see Section 29.2.1). Figure 18.2 shows what happens to a binary counter as it is incremented 16 times, starting with the initial value 0 and ending with the value 16. At the start of each iteration of the while loop in lines 2-4, we wish to add a 1 into position i. If A[i] = 1, then adding 1 flips the bit to 0 in position i and yields a carry of 1, to be added into position i + 1 on the next iteration of the loop. Otherwise, the loop ends, and then, if i < k, we know that A[i] = 0, so that adding a 1 into position i, flipping the 0 to a 1, is taken care of in line 6. The cost of each INCREMENT operation is linear in the number of bits flipped.
As with the stack example, a cursory analysis yields a bound that is correct but not tight. A single execution of INCREMENT takes time
We can tighten our analysis to yield a worst-case cost of O(n) for a sequence of n INCREMENT'S by observing that not all bits flip each time INCREMENT is called. As Figure 18.2 shows, A[0] does flip each time INCREMENT is called. The next-highest-order bit, A[1], flips only every other time: a sequence of n INCREMENT operations on an initially zero counter causes A[1] to flip
by equation (3.4). The worst-case time for a sequence of n INCREMENT operations on an initially zero counter is therefore O(n), so the amortized cost of each operation is O(n)/n = O(1).
18.1-1
If a MULTIPUSH operation were included in the set of stack operations, would the O(1) bound on the amortized cost of stack operations continue to hold?
18.1-2
Show that if a DECREMENT operation were included in the k-bit counter example, n operations could cost as much as
18.1-3
A sequence of n operations is performed on a data structure. The ith operation costs i if i is an exact power of 2, and 1 otherwise. Use an aggregate method of analysis to determine the amortized cost per operation.
In the accounting method of amortized analysis, we assign differing charges to different operations, with some operations charged more or less than they actually cost. The amount we charge an operation is called its amortized cost. When an operation's amortized cost exceeds its actual cost, the difference is assigned to specific objects in the data structure as credit. Credit can be used later on to help pay for operations whose amortized cost is less than their actual cost. Thus, one can view the amortized cost of an operation as being split between its actual cost and credit that is either deposited or used up. This is very different from the aggregate method, in which all operations have the same amortized cost.
One must choose the amortized costs of operations carefully. If we want analysis with amortized costs to show that in the worst case the average cost per operation is small, the total amortized cost of a sequence of operations must be an upper bound on the total actual cost of the sequence. Moreover, as in the aggregate method, this relationship must hold for all sequences of operations. Thus, the total credit associated with the data structure must be nonnegative at all times, since it represents the amount by which the total amortized costs incurred exceed the total actual costs incurred. If the total credit were ever allowed to become negative (the result of undercharging early operations with the promise of repaying the account later on), then the total amortized costs incurred at that time would be below the total actual costs incurred; for the sequence of operations up to that time, the total amortized cost would not be an upper bound on the total actual cost. Thus, we must take care that the total credit in the data structure never becomes negative.
To illustrate the accounting method of amortized analysis, let us return to the stack example. Recall that the actual costs of the operations were
where k is the argument supplied to MULTIPOP and s is the stack size when it is called. Let us assign the following amortized costs:
Note that the amortized cost of MULTIPOP is a constant (0), whereas the actual cost is variable. Here, all three amortized costs are O(l), although in general the amortized costs of the operations under consideration may differ asymptotically.
We shall now show that we can pay for any sequence of stack operations by charging the amortized costs. Suppose we use a dollar bill to represent each unit of cost. We start with an empty stack. Recall the analogy of Section 11.1 between the stack data structure and a stack of plates in a cafeteria. When we push a plate on the stack, we use 1 dollar to pay the actual cost of the push and are left with a credit of 1 dollar (out of the 2 dollars charged), which we put on top of the plate. At any point in time, every plate on the stack has a dollar of credit on it.
The dollar stored on the plate is prepayment for the cost of popping it from the stack. When we execute a POP operation, we charge the operation nothing and pay its actual cost using the credit stored in the stack. To pop a plate, we take the dollar of credit off the plate and use it to pay the actual cost of the operation. Thus, by charging the PUSH operation a little bit more, we needn't charge the POP operation anything.
Moreover, we needn't charge MULTIPOP operations anything either. To pop the first plate, we take the dollar of credit off the plate and use it to pay the actual cost of a POP operation. To pop a second plate, we again have a dollar of credit on the plate to pay for the POP operation, and so on. Thus, we have always charged at least enough up front to pay for MULTIPOP operations. In other words, since each plate on the stack has 1 dollar of credit on it, and the stack always has a nonnegative number of plates, we have ensured that the amount of credit is always nonnegative. Thus, for any sequence of n PUSH, POP, and MULTIPOP operations, the total amortized cost is an upper bound on the total actual cost. Since the total amortized cost is O(n), so is the total actual cost.
As another illustration of the accounting method, we analyze the INCREMENT operation on a binary counter that starts at zero. As we observed earlier, the running time of this operation is proportional to the number of bits flipped, which we shall use as our cost for this example. Let us once again use a dollar bill to represent each unit of cost (the flipping of a bit in this example).
For the amortized analysis, let us charge an amortized cost of 2 dollars to set a bit to 1. When a bit is set, we use 1 dollar (out of the 2 dollars charged) to pay for the actual setting of the bit, and we place the other dollar on the bit as credit. At any point in time, every 1 in the counter has a dollar of credit on it, and thus we needn't charge anything to reset a bit to 0; we just pay for the reset with the dollar bill on the bit.
The amortized cost of INCREMENT can now be determined. The cost of resetting the bits within the while loop is paid for by the dollars on the bits that are reset. At most one bit is set, in line 6 of INCREMENT, and therefore the amortized cost of an INCREMENT operation is at most 2 dollars. The number of l's in the counter is never negative, and thus the amount of credit is always nonnegative. Thus, for n INCREMENT operations, the total amortized cost is O(n), which bounds the total actual cost.
18.2-1
A sequence of stack operations is performed on a stack whose size never exceeds k. After every k operations, a copy of the entire stack is made for backup purposes. Show that the cost of n stack operations, including copying the stack, is O(n) by assigning suitable amortized costs to the various stack operations.
18.2-2
Redo Exercise 18.1-3 using an accounting method of analysis.
18.2-3
Suppose we wish not only to increment a counter but also to reset it to zero (i.e., make all bits in it 0). Show how to implement a counter as a bit vector so that any sequence of n INCREMENT and RESET operations takes time O(n) on an initially zero counter. (Hint: Keep a pointer to the high-order 1.)
Instead of representing prepaid work as credit stored with specific objects in the data structure, the potential method of amortized analysis represents the prepaid work as "potential energy,"or just "potential," that can be released to pay for future operations. The potential is associated with the data structure as a whole rather than with specific objects within the data structure.
The potential method works as follows. We start with an initial data structure D0 on which n operations are performed. For each i = 1, 2, . . . , n, we let ci be the actual cost of the ith operation and Di be the data structure that results after applying the ith operation to data structure Di - l. A potential function
The amortized cost of each operation is therefore its actual cost plus the increase in potential due to the operation. By equation (18.1), the total amortized cost of the n operations is
The second equality follows from equation (3.7), since the
If we can define a potential function
Intuitively, if the potential difference
The amortized costs defined by equations (18.1) and (18.2) depend on the choice of the potential function
To illustrate the potential method, we return once again to the example of the stack operations PUSH, POP, and MULTIPOP. We define the potential function
The total amortized cost of n operations with respect to
Let us now compute the amortized costs of the various stack operations. If the ith operation on a stack containing s objects is a PUSH operation, then the potential difference is
By equation (18.1), the amortized cost of this PUSH operation is
Suppose that the ith operation on the stack is MULTIPOP(S,k) and that k' = min(k,s) objects are popped off the stack. The actual cost of the operation is k', and the potential difference is
Thus, the amortized cost of the MULTIPOP operation is
Similarly, the amortized cost of an ordinary POP operation is 0.
The amortized cost of each of the three operations is O(1), and thus the total amortized cost of a sequence of n operations is O(n). Since we have already argued that
As another example of the otential method, we again look at incrementing a binary counter. This time, we define the potential of the counter after the ith INCREMENT operation to be bi, the number of 1's in the counter after the ith operation.
Let us compute the amortized cost of an INCREMENT operation. Suppose that the ith INCREMENT operation resets ti bits. The actual cost of the operation is therefore at most ti +1, since in addition to resetting ti bits, it sets at most one bit to a 1. The number of 1's in the counter after the ith operation is therefore bi
The amortized cost is therefore
If the counter starts at zero, then
The potential method gives us an easy way to analyze the counter even when it does not start at zero. There are initially b0 1's, and after n INCREMENT operations there are bn 1's, where 0
We have
Note in particular that since b0
18.3-1
Suppose we have a potential function
18.3-2
Redo Exercise 18.1-3 using a potential method of analysis.
18.3-3
Consider an ordinary binary heap data structure with n elements that supports the instructions INSERT and EXTRACT-MIN in O(lg n) worst-case time. Give a potential function
18.3-4
What is the total cost of executing n of the stack operations PUSH, POP, and MULTIPOP, assuming that the stack begins with s0 objects and finishes with sn objects?
18.3-5
Suppose that a counter begins at a number with b 1's in its binary representation, rather than at 0. Show that the cost of performing n INCREMENT operations is O( n) if n =
18.3-6
Show how to implement a queue with two ordinary stacks (Exercise 11.1-6) so that the amortized cost of each ENQUEUE and each DEQUEUE operation is O(1).
In some applications, we do not know in advance how many objects will be stored in a table. We might allocate space for a table, only to find out later that it is not enough. The table must then be reallocated with a larger size, and all objects stored in the original table must be copied over into the new, larger table. Similarly, if many objects have been deleted from the table, it may be worthwhile to reallocate the table with a smaller size. In this section, we study this problem of dynamically expanding and contracting a table. Using amortized analysis, we shall show that the amortized cost of insertion and deletion is only O(1), even though the actual cost of an operation is large when it triggers an expansion or a contraction. Moreover, we shall see how to guarantee that the unused space in a dynamic table never exceeds a constant fraction of the total space.
We assume that the dynamic table supports the operations TABLE-INSERT and TABLE-DELETE. TABLE-INSERT inserts into the table an item that occupies a single slot, that is, a space for one item. Likewise, TABLE-DELETE can be thought of as removing an item from the table, thereby freeing a slot. The details of the data-structuring method used to organize the table are unimportant; we might use a stack (Section 11.1), a heap (Section 7.1), or a hash table (Chapter 12). We might also use an array or collection of arrays to implement object storage, as we did in Section 11.3.
We shall find it convenient to use a concept introduced in our analysis of hashing (Chapter 12). We define the load factor
We start by analyzing a dynamic table in which only insertions are performed. We then consider the more general case in which both insertions and deletions are allowed.
Let us assume that storage for a table is allocated as an array of slots. A table fills up when all slots have been used or, equivalently, when its load factor is 1.1 In some software environments, if an attempt is made to insert an item into a full table, there is no alternative but to abort with an error. We shall assume, however, that our software environment, like many modern ones, provides a memory-management system that can allocate and free blocks of storage on request. Thus, when an item is inserted into a full table, we can expand the table by allocating a new table with more slots than the old table had and then copy items from the old table into the new one.
1In some situations, such as an open-address hash table, we may wish to consider a table to be full if its load factor equals some constant strictly less than 1. (See Exercise 18.4-2.)
A common heuristic is to allocate a new table that has twice as many slots as the old one. If only insertions are performed, the load factor of a table is always at least 1/2, and thus the amount of wasted space never exceeds half the total space in the table.
In the following pseudocode, we assume that T is an object representing the table. The field table[T] contains a pointer to the block of storage representing the table. The field num[T]contains the number of items in the table, and the field size[T] is the total number of slots in the table. Initially, the table is empty: num[T] = size[T] = 0.
Notice that we have two "insertion" procedures here: the TABLE-INSERT procedure itself and the elementary insertion into a table in lines 6 and 10. We can analyze the running time of TABLE-INSERT in terms of the number of elementary insertions by assigning a cost of 1 to each elementary insertion. We assume that the actual running time of TABLE-INSERT is linear in the time to insert individual items, so that the overhead for allocating an initial table in line 2 is constant and the overhead for allocating and freeing storage in lines 5 and 7 is dominated by the cost of transferring items in line 6. We call the event in which the then clause in lines 5-9 is executed an expansion.
Let us analyze a sequence of n TABLE-INSERT operations on an initially empty table. What is the cost ci of the ith operation? If there is room in the current table (or if this is the first operation), then ci = 1, since we need only perform the one elementary insertion in line 10. If the current table is full, however, and an expansion occurs, then ci = i: the cost is 1 for the elementary insertion in line 10 plus i - 1 for the items that must be copied from the old table to the new table in line 6. If n operations are performed, the worst-case cost of an operation is O(n), which leads to an upper bound of O(n2) on the total running time for n operations.
This bound is not tight, because the cost of expanding the table is not borne often in the course of n TABLE-INSERT operations. Specifically, the ith operation causes an expansion only when i - 1 is an exact power of 2. The amortized cost of an operation is in fact O(1), as we can show using the aggregate method. The cost of the ith operation is
The total cost of n TABLE-INSERT operations is therefore
since there are at most n operations that cost 1 and the costs of the remaining operations form a geometric series. Since the total cost of n TABLE-INSERT operations is 3n, the amortized cost of a single operation is 3.
By using the accounting method, we can gain some feeling for why the amortized cost of a TABLE-INSERT operation should be 3. Intuitively, each item pays for 3 elementary insertions: inserting itself in the current table, moving itself when the table is expanded, and moving another item that has already been moved once when the table is expanded. For example, suppose that the size of the table is m immediately after an expansion. Then, the number of items in the table is m/2, and the table contains no credit. We charge 3 dollars for each insertion. The elementary insertion that occurs immediately costs 1 dollar. Another dollar is placed as credit on the item inserted. The third dollar is placed as credit on one of the m/2 items already in the table. Filling the table requires m/2 additional insertions, and thus, by the time the table contains m items and is full, each item has a dollar to pay for its reinsertion during the expansion.
The potential method can also be used to analyze a sequence of n TABLE- INSERT operations, and we shall use it in Section 18.4.2 to design a TABLE-DELETE operation that has O(1) amortized cost as well. We start by defining a potential function
is one possibility. Immediately after an expansion, we have num[T] = size[T]/2, and thus
To analyze the amortized cost of the ith TABLE-INSERT operation, we let numi denote the number of items stored in the table after the ith operation, sizei denote the total size of the table after the ith operation, and
If the ith TABLE-INSERT operation does not trigger an expansion, then sizei = sizei - 1 and the amortized cost of the operation is
If the ith operation does trigger an expansion, then sizei/2 = sizei-1 = numi - 1, and the amortized cost of the operation is
Figure 18.3 plots the values of numi, sizei, and
To implement a TABLE-DELETE operation, it is simple enough to remove the specified item from the table. It is often desirable, however, to contract the table when the load factor of the table becomes too small, so that the wasted space is not exorbitant. Table contraction is analogous to table expansion: when the number of items in the table drops too low, we allocate a new, smaller table and then copy the items from the old table into the new one. The storage for the old table can then be freed by returning it to the memory-management system. Ideally, we would like to preserve two properties:
We assume that cost can be measured in terms of elementary insertions and deletions.
A natural strategy for expansion and contraction is to double the table size when an item is inserted into a full table and halve the size when a deletion would cause the table to become less than half full. This strategy guarantees that the load factor of the table never drops below 1/2, but unfortunately, it can cause the amortized cost of an operation to be quite large. Consider the following scenario. We perform n operations on a table T, where n is an exact power of 2. The first n/2 operations are insertions, which by our previous analysis cost a total of
where I stands for an insertion and D stands for a deletion. The first insertion causes an expansion of the table to size n. The two following deletions cause a contraction of the table back to size n/2. Two further insertions cause another expansion, and so forth. The cost of each expansion and contraction is
The difficulty with this strategy is obvious: after an expansion, we do not perform enough deletions to pay for a contraction. Likewise, after a contraction, we do not perform enough insertions to pay for an expansion.
We can improve upon this strategy by allowing the load factor of the table to drop below 1/2. Specifically, we continue to double the table size when an item is inserted into a full table, but we halve the table size when a deletion causes the table to become less than 1/4 full, rather than 1/2 full as before. The load factor of the table is therefore bounded below by the constant 1/4. The idea is that after an expansion, the load factor of the table is 1/2. Thus, half the items in the table must be deleted before a contraction can occur, since contraction does not occur unless the load factor would fall below 1/4. Likewise, after a contraction, the load factor of the table is also 1/2. Thus, the number of items in the table must be doubled by insertions before an expansion can occur, since expansion occurs only when the load factor would exceed 1.
We omit the code for TABLE-DELETE, since it is analogous to TABLE-INSERT. It is convenient to assume for analysis, however, that if the number of items in the table drops to 0, the storage for the table is freed. That is, if num[T] = 0, then size[T] = 0.
We can now use the potential method to analyze the cost of a sequence of n TABLE-INSERT and TABLE-DELETE operations. We start by defining a potential function
Observe that the potential of an empty table is 0 and that the potential is never negative. Thus, the total amortized cost of a sequence of operations with respect to
Before proceeding with a precise analysis, we pause to observe some properties of the potential function. Notice that when the load factor is 1/2, the potential is 0. When it is 1, we have size[T] = num[T], which implies
To analyze a sequence of n TABLE-INSERT and TABLE-DELETE operations, we let ci denote the actual cost of the ith operation,
We start with the case in which the ith operation is TABLE-INSERT. If
Thus, the amortized cost of a TABLE-INSERT operation is at most 3.
We now turn to the case in which the ith operation is TABLE-DELETE. In this case, numi = numi-1 - 1. If
If
When the ith operation is a TABLE-DELETE and
In summary, since the amortized cost of each operation is bounded above by a constant, the actual time for any sequence of n operations on a dynamic table is O(n).
18.4-1
Argue intuitively that if
18.4-2
Suppose that we wish to implement a dynamic, open-address hash table. Why might we consider the table to be full when its load factor reaches some value
18.4-3
Show that if the ith operation on a dynamic table is TABLE-DELETE and
18.4-4
Suppose that instead of contracting a table by halving its size when its load factor drops below 1/4, we contract it by multiplying its size by 2/3 when its load factor drops below 1/3. Using the potential function
show that the amortized cost of a TABLE-DELETE that uses this strategy is bounded above by a constant.
18-1 Bit-reversed binary counter
Chapter 32 examines an important algorithm called the Fast Fourier Transform, or FFT. The first step of the FFT algorithm performs a bit-reversal permutation on an input array A[0 . . n - 1] whose length is n = 2k for some nonnegative integer k. This permutation swaps elements whose indices have binary representations that are the reverse of each other.
We can express each index a as a k-bit sequence
thus,
For example, if n = 16 (or, equivalently, k = 4), then revk(3) = 12, since the 4-bit representation of 3 is 0011, which when reversed gives 1100, the 4-bit representation of 12.
a. Given a function revk that runs in
We can use an algorithm based on an amortized analysis to improve the running time of the bit-reversal permutation. We maintain a "bit-reversed counter " and a procedure BIT-REVERSED-INCREMENT that, when given a bit-reversed-counter value a, produces revk(revk(a) + 1). If k = 4, for example, and the bit-reversed counter starts at 0, then successive calls to BIT-REVERSED-INCREMENT produce the sequence
b. Assume that the words in your computer store k-bit values and that in unit time, your computer can manipulate the binary values with operations such as shifting left or right by arbitrary amounts, bitwise-AND, bitwise-OR, etc. Describe an implementation of the BIT-REVERSED-INCREMENT procedure that allows the bit-reversal permutation on an n-element array to be performed in a total of O(n) time.
c. Suppose that you can shift a word left or right by only one bit in unit time. Is it still possible to implement an O(n)-time bit-reversal permutation?
18-2 Making binary search dynamic
Binary search of a sorted array takes logarithmic search time, but the time to insert a new element is linear in the size of the array. We can improve the time for insertion by keeping several sorted arrays.
Specifically, suppose that we wish to support SEARCH and INSERT on a set of n elements. Let k =
a. Describe how to perform the SEARCH operation for this data structure. Analyze its worst-case running time.
b. Describe how to insert a new element into this data structure. Analyze its worst-case and amortized running times.
c. Discuss how to implement DELETE.
18-3 Amortized weight-balanced trees
Consider an ordinary binary search tree augmented by adding to each node x the field size[x] giving the number of keys stored in the subtree rooted at x. Let
and
The tree as a whole is
a. A 1/2-balanced tree is, in a sense, as balanced as it can be. Given a node x in an arbitrary binary search tree, show how to rebuild the subtree rooted at x so that it becomes 1/2-balanced. Your algorithm should run in time
b. Show that performing a search in an n-node
For the remainder of this problem, assume that the constant
We shall analyze this rebuilding scheme using the potential method. For a node x in a binary search tree T, we define
and we define the potential of T as
where c is a sufficiently large constant that depends on
c. Argue that any binary search tree has nonnegative potential and that a 1/2-balanced tree has potential 0.
d. Suppose that m units of potential can pay for rebuilding an m-node subtree. How large must c be in terms of
e. Show that inserting a node into or deleting a node from an n-node
The aggregate method of amortized' analysis was used by Aho, Hopcroft, and Ullman [4]. Tarjan [189] surveys the accounting and potential methods of amortized analysis and presents several applications. He attributes the accounting method to several authors, including M. R. Brown, R. E. Tarjan, S. Huddleston, and K. Mehlhorn. He attributes the potential method to D. D. Sleator. The term "amortized" is due to D. D. Sleator and R. E. Tarjan.
Stack operations
 (n).
(n).MULTIPOP(S,k)
1 while not STACK-EMPTY(S) and k
 0
02 do POP(S)
3 k
 k - 1
k - 1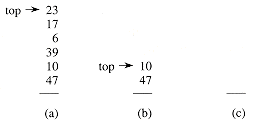
Figure 18.1 The action of MULTIPOP on a stack S, shown initially in (a). The top 4 objects are popped by MULTIPOP(S, 4), whose result is shown in (b). The next operation is MULTIPOP(S, 7), which empties the stack
 shown in (c)
shown in (c) since there were fewer than 7 objects remaining.
since there were fewer than 7 objects remaining.Incrementing a binary counter
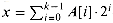 . Initially, x = 0, and thus A[i] = 0 for i = 0, 1, . . . , k - 1. To add 1 (modulo 2k) to the value in the counter, we use the following procedure.
. Initially, x = 0, and thus A[i] = 0 for i = 0, 1, . . . , k - 1. To add 1 (modulo 2k) to the value in the counter, we use the following procedure.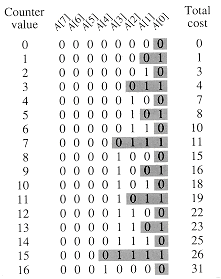
Figure 18.2 An 8-bit binary counter as its value goes from 0 to 16 by a sequence of 16 INCREMENT operations. Bits that flip to achieve the next value are shaded. The running cost for flipping bits is shown at the right. Notice that the total cost is never more than twice the total number of INCREMENT operations.
INCREMENT(A)
1 i
 0
02 while i< length[A] and A[i] = 1
3 do A[i]
 0
04 i
 i + 1
i + 15 if i < length[A]
6 then A[i]
 1
1 (k) in the worst case, in which array A contains all 1's. Thus, a sequence of n INCREMENT operations on an initially zero counter takes time O(nk) in the worst case.
(k) in the worst case, in which array A contains all 1's. Thus, a sequence of n INCREMENT operations on an initially zero counter takes time O(nk) in the worst case. n/2
n/2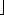 times. Similarly, bit A[2] flips only every fourth time, or
times. Similarly, bit A[2] flips only every fourth time, or 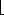 n/4
n/4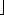 times in a sequence of n INCREMENT'S. In general, for i = 0, 1, . . . ,
times in a sequence of n INCREMENT'S. In general, for i = 0, 1, . . . , 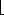 lg n
lg n , bit A[i] flips
, bit A[i] flips  n/2i
n/2i times in a sequence of n INCREMENT operations on an initially zero counter. For i >
times in a sequence of n INCREMENT operations on an initially zero counter. For i >  lg n
lg n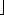 , bit A[i] never flips at all. The total number of flips in the sequence is thus
, bit A[i] never flips at all. The total number of flips in the sequence is thus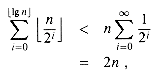
Exercises
 (nk) time.
(nk) time.18.2 The accounting method
Stack operations
PUSH 1 ,
POP 1 ,
MULTIPOP min(k,s) ,
PUSH 2 ,
POP 0 ,
MULTIPOP 0 .
Incrementing a binary counter
Exercises
18.3 The potential method
 maps each data structure Di to a real number
maps each data structure Di to a real number  (Di), which is the potential associated with data structure Di. The amortized cost
(Di), which is the potential associated with data structure Di. The amortized cost 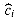 of the ith operation with respect to potential function
of the ith operation with respect to potential function  is defined by
is defined by
(18.1)
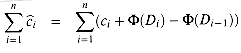

(18.2)
 (Di) telescope.
(Di) telescope. so that
so that  (Dn)
(Dn) 
 (D0), then the total amortized cost
(D0), then the total amortized cost 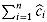 is an upper bound on the total actual cost. In practice, we do not always know how many operations might be performed. Therefore, if we require that
is an upper bound on the total actual cost. In practice, we do not always know how many operations might be performed. Therefore, if we require that  (Di)
(Di) 
 (D0) for all i, then we guarantee, as in the accounting method, that we pay in advance. It is often convenient to define
(D0) for all i, then we guarantee, as in the accounting method, that we pay in advance. It is often convenient to define  (D0) to be 0 and then to show that
(D0) to be 0 and then to show that  (Di)
(Di)  0 for all i. (See Exercise 18.3-1 for an easy way to handle cases in which
0 for all i. (See Exercise 18.3-1 for an easy way to handle cases in which  (D0)
(D0)  0.)
0.) (Di) -
(Di) -  (Di - 1) of the ith operation is positive, then the amortized cost
(Di - 1) of the ith operation is positive, then the amortized cost 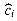 represents an overcharge to the ith operation, and the potential of the data structure increases. If the potential difference is negative, then the amortized cost represents an undercharge to the ith operation, and the actual cost of the operation is paid by the decrease in the potential.
represents an overcharge to the ith operation, and the potential of the data structure increases. If the potential difference is negative, then the amortized cost represents an undercharge to the ith operation, and the actual cost of the operation is paid by the decrease in the potential. . Different potential functions may yield different amortized costs yet still be upper bounds on the actual costs. There are often trade-offs that can be made in choosing a potential function; the best potential function to use depends on the desired time bounds.
. Different potential functions may yield different amortized costs yet still be upper bounds on the actual costs. There are often trade-offs that can be made in choosing a potential function; the best potential function to use depends on the desired time bounds.Stack operations
 on a stack to be the number of objects in the stack. For the empty stack D0 with which we start, we have
on a stack to be the number of objects in the stack. For the empty stack D0 with which we start, we have  (D0) = 0. Since the number of objects in the stack is never negative, the stack Di that results after the ith operation has nonnegative potential, and thus
(D0) = 0. Since the number of objects in the stack is never negative, the stack Di that results after the ith operation has nonnegative potential, and thus (Di)
(Di)  0
0=
 (D0).
(D0). therefore represents an upper bound on the actual cost.
therefore represents an upper bound on the actual cost. (Di) -
(Di) -  (Di - 1) = (s + 1 ) - s
(Di - 1) = (s + 1 ) - s= 1 .
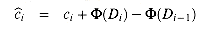
 (Di) -
(Di) -  (Di-1) = -k'.
(Di-1) = -k'.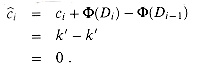
 (Di)
(Di) 
 (D0), the total amortized cost of n operations is an upper bound on the total actual cost. The worst-case cost of n operations is therefore O(n).
(D0), the total amortized cost of n operations is an upper bound on the total actual cost. The worst-case cost of n operations is therefore O(n).Incrementing a binary counter
 bi-1 - ti +1, and the potential difference is
bi-1 - ti +1, and the potential difference is (Di) -
(Di) -  (Di-1)
(Di-1)  (bi-1 - ti + 1) - bi-1
(bi-1 - ti + 1) - bi-1= 1 - ti.
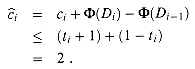
 (D0) = 0. Since
(D0) = 0. Since  (Di)
(Di)  0 for all i, the total amortized cost of a sequence of n INCREMENT operations is an upper bound on the total actual cost, and so the worst-case cost of n INCREMENT operations is O(n).
0 for all i, the total amortized cost of a sequence of n INCREMENT operations is an upper bound on the total actual cost, and so the worst-case cost of n INCREMENT operations is O(n). b0, bn
b0, bn  k. We can rewrite equation (18.2) as
k. We can rewrite equation (18.2) as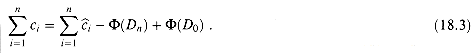
(18.3)
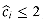 for all 1
for all 1  i
i  n. Since
n. Since  (D0) = b0 and
(D0) = b0 and  (Dn) = bn, the total actual cost of n INCREMENT operations is
(Dn) = bn, the total actual cost of n INCREMENT operations is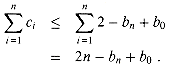
 k, if we execute at least n =
k, if we execute at least n = 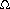 (k) INCREMENT operations, the total actual cost is O(n), no matter what initial value the counter contains.
(k) INCREMENT operations, the total actual cost is O(n), no matter what initial value the counter contains.Exercises
 such that
such that  (Di)
(Di) 
 (D0) for all i, but
(D0) for all i, but  (D0)
(D0)  0. Show that there exists a potential function
0. Show that there exists a potential function  ' such that
' such that  '(D0) = 0,
'(D0) = 0,  '(Di)
'(Di)  0 for all i
0 for all i  1, and the amortized costs using
1, and the amortized costs using  ' are the same as the amortized costs using
' are the same as the amortized costs using  .
. such that the amortized cost of INSERT is O(lg n) and the amortized cost of EXTRACT-MIN is O(1), and show that it works.
such that the amortized cost of INSERT is O(lg n) and the amortized cost of EXTRACT-MIN is O(1), and show that it works.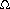 (b). (Do not assume that b is constant.)
(b). (Do not assume that b is constant.)18.4 Dynamic tables
 (T) of a nonempty table T to be the number of items stored in the table divided by the size (number of slots) of the table. We assign an empty table (one with no items) size 0, and we define its load factor to be 1. If the load factor of a dynamic table is bounded below by a constant, the unused space in the table is never more than a constant fraction of the total amount of space.
(T) of a nonempty table T to be the number of items stored in the table divided by the size (number of slots) of the table. We assign an empty table (one with no items) size 0, and we define its load factor to be 1. If the load factor of a dynamic table is bounded below by a constant, the unused space in the table is never more than a constant fraction of the total amount of space.18.4.1 Table expansion
TABLE-INSERT(T,x)
1 if size[T] = 0
2 then allocate table [T] with 1 slot
3 size[T]
 1
14 if num[T] = size[T]
5 then allocate new-table with 2
 size[T] slots
size[T] slots6 insert all items in table[T] into new-table
7 free table[T]
8 table[T]
 new-table
new-table9 size[T]
 2
2  size[T]
size[T]10 insert x into table[T]
11 num[T]
 num[T] + 1
num[T] + 1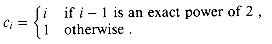
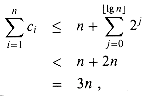
 that is 0 immediately after an expansion but builds to the table size by the time the table is full, so that the next expansion can be paid for by the potential. The function
that is 0 immediately after an expansion but builds to the table size by the time the table is full, so that the next expansion can be paid for by the potential. The function (T) = 2
(T) = 2 num[T] - size[T]
num[T] - size[T](18.4)
 (T) = 0, as desired. Immediately before an expansion, we have num[T] = size[T], and thus
(T) = 0, as desired. Immediately before an expansion, we have num[T] = size[T], and thus  (T) = num[T], as desired. The initial value of the potential is 0, and since the table is always at least half full, num[T]
(T) = num[T], as desired. The initial value of the potential is 0, and since the table is always at least half full, num[T]  size[T]/2, which implies that
size[T]/2, which implies that  (T) is always nonnegative. Thus, the sum of the amortized costs of n TABLE-INSERT operations is an upper bound on the sum of the actual costs.
(T) is always nonnegative. Thus, the sum of the amortized costs of n TABLE-INSERT operations is an upper bound on the sum of the actual costs. i denote the potential after the ith operation. Initially, we have num0 = 0, size0 =0, and
i denote the potential after the ith operation. Initially, we have num0 = 0, size0 =0, and  0 = 0.
0 = 0.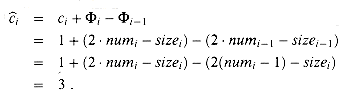
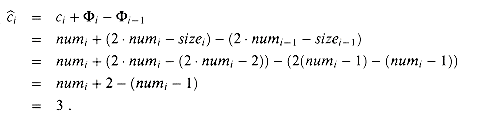
 i against i. Notice how the potential builds to pay for the expansion of the table.
i against i. Notice how the potential builds to pay for the expansion of the table.18.4.2 Table expansion and contraction
 the load factor of the dynamic table is bounded below by a constant, and
the load factor of the dynamic table is bounded below by a constant, and the amortized cost of a table operation is bounded above by a constant.
the amortized cost of a table operation is bounded above by a constant.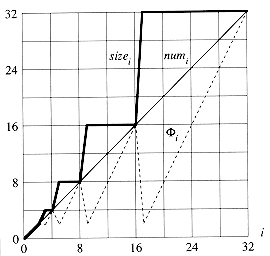
Figure 18.3 The effect of a sequence of n TABLE-INSERT operations on the number numi of items in the table, the number sizei of slots in the table, and the potential
 i = 2
i = 2  numi - sizei, each being measured after the ith operation. The thin line shows numi, the thick line shows sizei, and the dashed line shows
numi - sizei, each being measured after the ith operation. The thin line shows numi, the thick line shows sizei, and the dashed line shows  i. Notice that immediately before an expansion, the potential has built up to the number of items in the table, and therefore it can pay for moving all the items to the new table. Afterwards, the potential drops to 0, but it is immediately increased by 2 when the item that caused the expansion is inserted.
i. Notice that immediately before an expansion, the potential has built up to the number of items in the table, and therefore it can pay for moving all the items to the new table. Afterwards, the potential drops to 0, but it is immediately increased by 2 when the item that caused the expansion is inserted. (n). At the end of this sequence of insertions, num[T] = size[T] = n/2. For the second n/2 operations, we perform the following sequence:
(n). At the end of this sequence of insertions, num[T] = size[T] = n/2. For the second n/2 operations, we perform the following sequence:I, D, D, I, I, D, D, I, I,... ,
 (n), and there are
(n), and there are  (n) of them. Thus, the total cost of the n operations is
(n) of them. Thus, the total cost of the n operations is  (n2), and the amortized cost of an operation is
(n2), and the amortized cost of an operation is  (n).
(n). that is 0 immediately after an expansion or contraction and builds as the load factor increases to 1 or decreases to 1/4. Let us denote the load factor of a nonempty table T by
that is 0 immediately after an expansion or contraction and builds as the load factor increases to 1 or decreases to 1/4. Let us denote the load factor of a nonempty table T by  (T) = num[T]/size[T]. Since for an empty table, num[T] = size[T] = 0 and
(T) = num[T]/size[T]. Since for an empty table, num[T] = size[T] = 0 and  [T] = 1, we always have num[T] =
[T] = 1, we always have num[T] =  (T)
(T)  size[T], whether the table is empty or not. We shall use as our potential function
size[T], whether the table is empty or not. We shall use as our potential function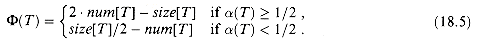
(18.5)
 is an upper bound on their actual cost.
is an upper bound on their actual cost. (T) = num[T], and thus the potential can pay for an expansion if an item is inserted. When the load factor is 1/4, we have size[T] = 4
(T) = num[T], and thus the potential can pay for an expansion if an item is inserted. When the load factor is 1/4, we have size[T] = 4  num[T] , which implies
num[T] , which implies  (T) = num[T], and thus the potential can pay for a contraction if an item is deleted. Figure 18.4 illustrates how the potential behaves for a sequence of operations.
(T) = num[T], and thus the potential can pay for a contraction if an item is deleted. Figure 18.4 illustrates how the potential behaves for a sequence of operations.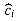 denote its amortized cost with respect to
denote its amortized cost with respect to  , numi denote the number of items stored in the table after the ith operation, sizei denote the total size of the table after the ith operation,
, numi denote the number of items stored in the table after the ith operation, sizei denote the total size of the table after the ith operation,  i denote the load factor of the table after the ith operation, and
i denote the load factor of the table after the ith operation, and  i denote the potential after the ith operation. Initially, num0 = 0, size0 = 0,
i denote the potential after the ith operation. Initially, num0 = 0, size0 = 0,  0 = 1, and
0 = 1, and  0 = 0.
0 = 0.
Figure 18.4 The effect of a sequence of n TABLE-INSERT and TABLE-DELETE operations on the number numi of items in the table, the number sizei of slots in the table, and the potential
each being measured after the ith operation. The thin line shows numi, the thick line shows sizei, and the dashed line shows
 i. Notice that immediately before an expansion, the potential has built up to the number of items in the table, and therefore it can pay for moving all the items to the new table. Likewise, immediately before a contraction, the potential has built up to the number of items in the table.
i. Notice that immediately before an expansion, the potential has built up to the number of items in the table, and therefore it can pay for moving all the items to the new table. Likewise, immediately before a contraction, the potential has built up to the number of items in the table. i-1
i-1 1/2, the analysis is identical to that for table expansion in Section 18.4.1. Whether the table expands or not, the amortized cost
1/2, the analysis is identical to that for table expansion in Section 18.4.1. Whether the table expands or not, the amortized cost 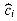 of the operation is at most 3. If
of the operation is at most 3. If  i-1 < 1/2, the table cannot expand as a result of the operation, since expansion occurs only when
i-1 < 1/2, the table cannot expand as a result of the operation, since expansion occurs only when  i-1 = 1. If
i-1 = 1. If  i < 1/2 as well, then the amortized cost of the ith operation is
i < 1/2 as well, then the amortized cost of the ith operation is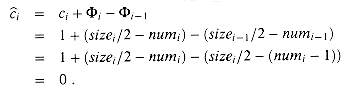
If
 i-1 < 1/2 but
i-1 < 1/2 but  i
i  1/2, then
1/2, then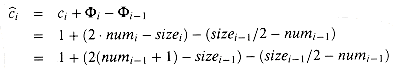
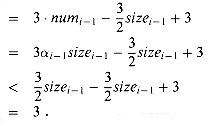
 i-1 < 1/2, then we must consider whether the operation causes a contraction. If it does not, then sizei = sizei-1 and the amortized cost of the operation is
i-1 < 1/2, then we must consider whether the operation causes a contraction. If it does not, then sizei = sizei-1 and the amortized cost of the operation is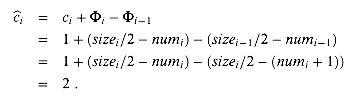
 i-1 < 1/2 and the ith operation does trigger a contraction, then the actual cost of the operation is ci = numi + 1, since we delete one item and move numi items. We have sizei/2 = sizei-1/4 = numi + 1, and the amortized cost of the operation is
i-1 < 1/2 and the ith operation does trigger a contraction, then the actual cost of the operation is ci = numi + 1, since we delete one item and move numi items. We have sizei/2 = sizei-1/4 = numi + 1, and the amortized cost of the operation is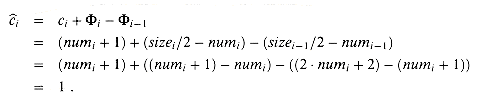
 i-1
i-1  1/2, the amortized cost is also bounded above by a constant. The analysis is left as Exercise 18.4-3.
1/2, the amortized cost is also bounded above by a constant. The analysis is left as Exercise 18.4-3.Exercises
 i-1
i-1  1/2 and
1/2 and  i
i  1/2, then the amortized cost of a TABLE-INSERT operation is 0.
1/2, then the amortized cost of a TABLE-INSERT operation is 0. that is strictly less than 1? Describe briefly how to make insertion into a dynamic, open-address hash table run in such a way that the expected value of the amortized cost per insertion is O(1). Why is the expected value of the actual cost per insertion not necessarily O(1) for all insertions?
that is strictly less than 1? Describe briefly how to make insertion into a dynamic, open-address hash table run in such a way that the expected value of the amortized cost per insertion is O(1). Why is the expected value of the actual cost per insertion not necessarily O(1) for all insertions? i-1
i-1  1/2, then the amortized cost of the operation with respect to the potential function (18.5) is bounded above by a constant.
1/2, then the amortized cost of the operation with respect to the potential function (18.5) is bounded above by a constant. (T) = |2
(T) = |2  num[T] - size[T]| ,
num[T] - size[T]| ,Problems
 ak-1, ak-2, . . . , a0
ak-1, ak-2, . . . , a0 , where
, where 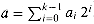 . We define
. We definerevk(
 ak-1, ak-2,..., a0
ak-1, ak-2,..., a0 ) = (
) = ( a0, a1,..., ak-1
a0, a1,..., ak-1 ;
;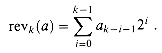
 (k) time, write an algorithm to perform the bit-reversal permutation on an array of length n = 2k in O(nk) time.
(k) time, write an algorithm to perform the bit-reversal permutation on an array of length n = 2k in O(nk) time.0000, 1000, 0100, 1100, 0010, 1010,... = 0, 8, 4, 12, 2, 10,... .
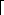 lg(n + 1)
lg(n + 1)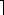 , and let the binary representation of n be
, and let the binary representation of n be  nk-1, nk-2, . . . , n0
nk-1, nk-2, . . . , n0 . We have k sorted arrays A0, A1, . . . , Ak-1, where for i = 0, 1, . . . , k - 1, the length of array Ai is 2i. Each array is either full or empty, depending on whether ni = 1 or ni = 0, respectively. The total number of elements held in all k arrays is therefore
. We have k sorted arrays A0, A1, . . . , Ak-1, where for i = 0, 1, . . . , k - 1, the length of array Ai is 2i. Each array is either full or empty, depending on whether ni = 1 or ni = 0, respectively. The total number of elements held in all k arrays is therefore 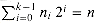 . Although each individual array is sorted, there is no particular relationship between elements in different arrays.
. Although each individual array is sorted, there is no particular relationship between elements in different arrays. be a constant in the range 1/2
be a constant in the range 1/2 
 < 1. We say that a given node x is
< 1. We say that a given node x is  -balanced if
-balanced ifsize[left[x]]

 . size[x]
. size[x]size[right[x]]

 . size[x].
. size[x]. -balanced if every node in the tree is
-balanced if every node in the tree is  -balanced. The following amortized approach to maintaining weight-balanced trees was suggested by G. Varghese.
-balanced. The following amortized approach to maintaining weight-balanced trees was suggested by G. Varghese. (size[x], and it can use O(size[x]) auxiliary storage.
(size[x], and it can use O(size[x]) auxiliary storage. -balanced binary search tree takes O(lg n) worst-case time.
-balanced binary search tree takes O(lg n) worst-case time. is strictly greater than 1/2. Suppose that INSERT and DELETE are implemented as usual for an n-node binary search tree, except that after every such operation, if any node in the tree is no longer
is strictly greater than 1/2. Suppose that INSERT and DELETE are implemented as usual for an n-node binary search tree, except that after every such operation, if any node in the tree is no longer  -balanced, then the subtree rooted at the highest such node in the tree is "rebuilt" so that it becomes 1/2-balanced.
-balanced, then the subtree rooted at the highest such node in the tree is "rebuilt" so that it becomes 1/2-balanced.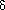 (x) = |size[left[x]] - size[right[x]]| ,
(x) = |size[left[x]] - size[right[x]]| ,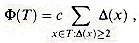
 .
. in order for it to take O(1) amortized time to rebuild a subtree that is not
in order for it to take O(1) amortized time to rebuild a subtree that is not  -balanced?
-balanced? -balanced tree costs O(lg n) amortized time.
-balanced tree costs O(lg n) amortized time.Chapter notes


