12.1 INTRODUCTION
This chapter explores one aspect of how information retrieval systems efficiently process user requests. Most systems rely heavily on the ability to perform Boolean operations. User requests are typically phrased in terms of Boolean operations. Hence, the ability to translate them into a form that may be speedily evaluated is of paramount importance. Techniques for doing so form the subject of this chapter.
Information retrieval systems manage documents. These differ from the data stored in traditional database management systems in that they have much less structure. The data are not organized into neat little units with uniform content, where an integer may be expected at a particular location or a string at another. Little may be reliably determined beyond the existence of a document and its boundaries. Of course, information may be derived from a document (such as inverted indices--see Chapter 3). However, such information is invisible to the user of an information retrieval system. He or she sees only a document, with no particular structure save units derived from natural languages, such as words, sentences, or paragraphs.
This creates a problem for information retrieval systems: queries tend to be vague, especially when compared to database management systems. The latter, with their precise characterization of data, permit a broad range of queries that can exploit known properties of the data. Thus, while a database management system user might issue a query such as:
select Name, Age from Person where Age > 25
the user of an information retrieval system has far less flexibility. The information retrieval system cannot hope to determine what sequence of characters in the documents under consideration represent age. It has no knowledge of document structure and therefore cannot make inferences about portions of a document.
Queries on documents in information retrieval systems, then, are limited to operations involving character strings, at best with some knowledge of sentence structure. A typical query might be, "Give me the names of all documents containing sentences with the words 'computer' and 'science'." Despite its seeming simplicity, such a query can be very costly. In a database management system, one might optimize this query by working from sorted data, and using search algorithms that capitalize on such order. An information retrieval system, however, cannot reorder a document's text. A search for a word within a document may therefore take time linearly proportional to the size of the document. As mentioned, the situation can be improved through the use of indices, but the use of a partial index can limit the flexibility of an information retrieval system, and a full index is often prohibitively expensive.
In any case, the size of the data is often enormous. Information retrieval systems manipulate huge amounts of information, often orders of magnitude more than is found in database management systems. Even if indexing is used, the data sets will be prohibitively large. Simple-minded algorithms to process queries will take unacceptable amounts of time and space.
Boolean operations are the key to describing queries, and their efficient implementation is essential. The typical technique is to use sets. This chapter covers how to implement Boolean operations as sets, and also how to efficiently implement set operations. It emhasizes sets that are expected to contain large numbers of elements. Section 12.2 discussess Boolean operations in more detail, describing precisely their relationship to sets. Section 12.3 presents an abstraction of sets. Sections 12.5 and 12.6 present various implementations of this abstraction. The final section analyzes the run-time properties of the implementation approaches.
Boolean expressions are formed from user queries. In some information retrieval systems, the user enters them directly. In more sophisticated systems, the user enters natural language, which the system converts into Boolean expressions. In any event, they are then evaluated to determine the results of the query. This section will show how Boolean expressions are built from queries, and how those expressions are translated into sets.
An information retrieval system accesses some set of documents. The system must be able to uniquely identify each document. In this chapter, it will suffice to have documents named doc1, doc2, . . . , docn. It is assumed that the name "doci" provides enough information to locate the information associated with document i. In reality, an addressing table would probably be associated with the names of documents, linking each name to some disk location, but this detail can be safely ignored for now.
Boolean expressions are formed from queries. They represent a request to determine what documents contain (or do not contain) a given set of keywords. For example
Find all documents containing "information".
is a query that, when evaluated, should yield a (possibly empty) set of documents, each of which contains the word "information" somewhere within its body. Most of the words in the sentence are noise, however. By definition, a query searches a set of documents to determine their content. The above is therefore usually represented as the Boolean expression:
information
which means, "A set whose elements are the names of all documents containing the pattern "information"."
Some queries attempt to find documents that do not contain a particular pattern, a fact that the corresponding Boolean expression must indicate. This is done using a "not" operator, prefixed to the expression. For example, the query:
is represented as the Boolean expression:
Most queries involve searching more than one term. For example, a user might say any of the following:
Only documents containing both "information" and "retrieval" will satisfy the first query, whereas the second will be satisfied by a document that contains either of the two words. Documents satisfying the third query are a subset of those that satisfy the second. In fact, those documents in the second query are the union of the documents in the first and third.
Each of the above queries illustrates a particular concept that may form a Boolean expression. These concepts are, respectively, conjunction, disjunction, and exclusive disjunction. They are represented in Boolean expressions using the operators and, or, and xor. The queries above would therefore be:
information and retrieval
information or retrieval
information xor retrieval
Boolean expressions may be formed from other Boolean expressions to yield rather complex structures. Consider the following query:
This translates into the following Boolean expression:
Parentheses are often helpful to avoid ambiguity.
Each portion of a Boolean expression yields a set of documents. These portions are evaluated separately, then simplified using techniques that will be discussed in this chapter. That is, "all documents containing 'information' " yields a set of documents D1, and "all documents containing 'retrieval' " yields some set D2. The information retrieval system must combine these two sets to yield the set D3 that contains only documents with both "information" and "retrieval."
The reader may be wondering how certain complex queries are handled. For instance, how is "all documents containing 'information' and 'retrieval' in the same sentence" represented as a Boolean expression? This question will be answered in other chapters. The concern of this chapter is not to study techniques for determining if a document contains a pattern. Rather, given a set of documents known to contain a pattern, the issue at hand is how to combine those patterns efficiently to answer a larger query. In other words, other chapters will discuss how to determine which documents contain "information," and which contain "retrieval." Here, the assumption is that the respective sets are known; the issue is how to combine those sets to determine what documents might contain both, either, or neither.
Combining the terms of Boolean expressions is conceptually quite simple. It involves sequences of familiar set operations. Let U represent the names of all documents stored. Let D1 and D2 represent the names of those documents that contain patterns P1 and P2, respectively. The following list defines how to evaluate Boolean expression operators in terms of the sets:
1. U - D1 is the set of all documents not containing P1 (not).
2. D1
3. D1
4. D1
The following example illustrates these expressions. Consider a set of five documents, and suppose that they contain the terms shown in Figure 12.1. The expressions given above will now be evaluated using the data in Figure 12.1. For instance, the Boolean expression "information" is the names of all documents containing the term "information":
{doc1, doc3}
The expression "information and retrieval" is:
{doc1, doc3}
whereas "information or retrieval" is:
{doc1, doc3}
As a more complex example:
{information and retrieval} or not {retrieval and science}
is:
({doc1, doc3}
- ({doc1, doc2}
= {doc2}
= {doc1, doc2, doc3, doc4, doc5}
Before discussing how to implement sets, it is necessary to define them more precisely. Sets are a familiar concept, and implementations for them may be found in many data structures textbooks. However, no two textbooks seem to have precisely the same operations, and the semantics of the operations vary from book to book (Does an operation modify its inputs? Is it a procedure or a function?). A little time spent discussing the meaning of a set as used in this chapter will avoid confusion.
A set is a homogeneous, unordered collection of elements. In programming language terms, a set has an associated "element data type," and all elements of the set must be of this type. Each element data type has a key. For a given set, no two elements ever simultaneously possess the same key. An element data type may also specify other data that will be included along with the element. These data values need not be unique among all elements of a set. If the key constitutes the entire value of a set element, however, then by definition all values in a set differ.
From the discussion in the previous section, it should be no surprise that the familiar set operations of union, intersection, and difference will be required. However, certain supporting operations will be necessary to provide a satsifactory algorithmic implementation of sets. The presentation will be done using the information hiding principle advanced by Parnas (1972), wherein a set is presented in two parts--a collection of access programs that define the operations a program may legally perform on a set, and an implementation for those programs.
To specify a set, one must provide an element data type E. This specifies the types of elements that may populate a given instance of a set. Some programming languages, such as Ada, permit programmers to enforce the constraint that a set contain homogeneous data. In C, the programming language used here, this constraint is unenforceable. However, only a little care is required to ensure that sets are in fact homogeneous.
The first order of business is to declare a data type for a set, and for elements of the set:
The structure of a set will be defined later, when the implementation is given. For now, it suffices to know that such a type is available. The definition for element types will depend on the type of data to be stored in the set. In C, it is generally possible to use the type "char*" to store data of any type. However, creating typespecific operations is usually better practice. Moreover, one implementation for sets given here cannot easily represent pointer data; in fact, short would be the best choice. This point will be discussed in more detail in each implementation.
Figure 12.2 shows the operations that constitute the interface to a set. A few conventions will be used that should be noted now:
1. All operations use pointers to values of type set. In C, pointer-valued parameters are generally used for parameters that a routine is to modify, or for efficiency. Here, the reason is usually efficiency. An operation does not modify its parameter unless so noted.
2. The existence of a Boolean data type is assumed. This type may be easily declared using the facilities of the C preprocessor:
3. The system using the sets will not modify element values once they have been inserted into a set. This problem might arise in C if a set contained strings. Consider the following:
Unless Insert has stored a copy of the string, the value of v will change inside s, since s will contain a pointer to the string rather than a unique value. This problem can be solved easily in two ways:
a. The application will agree not to modify values that are used in sets.
b. The specification of a set can include a function that creates a copy of a datum.
Case a turns out to suffice for information retrieval. Since it is simpler, it will be used in this chapter.
4. Unless explicitly stated otherwise, a set variable may not appear twice in a parameter list. That is, neither of the following are legal:
This restriction is actually not necessary for all routines, but occurs frequently enough to warrant its inclusion.
Most of the operations are self-explanatory, as they implement familiar set functions. The Iterate operation may require some explanation. Once a Boolean expression has been evaluated, the information retrieval system will need to determine all elements in the set. The system should not depend on a particular implementation of sets, so it must have some other means to access all elements. This is exactly what Iterate provides. The system will call it, supplying as a parameter a C routine that accomplishes some desired function. Iterate will execute this function once for every element in the set, supplying the element to the routine as a parameter. For example, suppose a developer writes the following C procedure:
The following statement would then print all elements of a set S of integers:
No qualifications are made about the order of the elements in the iteration; it is completely random so far as the routine calling Iterate is concerned. The only guarantee is that each element in the set is passed to f () exactly once.
It will be possible to pass parameters to the operations that would, if accepted, result in an erroneous set. Some error-handling mechanism is therefore needed. This mechanism must allow an information retrieval system to detect when an error has occurred. The Error_Occurred () routine, which can be used to check the status of an operation, achieves this. Its value is TRUE if an error occurred during the last executed set operation, and FALSE if no error occurred. A system that wished to check the validity of each operation might contain code such as the following:
The error handling will be accomplished such that a set will always be valid according to the rules of its implementation, even if an error occurred. Applications may therefore attempt corrective action and try again.
The interface given in Figure 12.2 can provide an information retrieval system with operations on sets of various types. These operations may be used by many parts of the system. Their packaging must make this expedient. Information retrieval systems are large and consist of many subsystems. The code for a typical information retrieval system will probably be spread throughout many files. The set operations must be packaged such that each subsystem--that is, set of files--needing access to sets may have them in the simplest possible way, involving no duplication of code.
The usual C technique for doing this is to package the interface in an "include file" (see Kernighan and Ritchie [1988]). This file contains specifications of the types, constants, and procedures that make up the set package, but omits any executable code. (The one exception is routines implemented as macros, rather than procedures. Their expansion, which includes executable code, appears in the include file.)
An implementation of a set would therefore be packaged as follows:
1. An include file, which might be named "set. h". It would contain all of Figure 12.2, plus the type definition and accompanying constants for the set data type. (Ideally the definition of the type would not be in the interface, but C discourages this.)
2. A file containing implementations of the routines, which might be named "set. c". Since set. h contains certain type definitions needed in the implementation, it begins with the line:
The routines' use will be illustrated by using them to solve the query given at the end of section 12.2. Doing so requires the use of six sets--three for each of the patterns, plus three to hold intermediate values and the results. Figure 12.3 gives the code. The issue of how the sets are initialized is ignored here; it is the subject of Chapter 3. That would involve calls to the Insert routine, one for each document to be inserted in a set.
Note that the code has been given independently from the implementation. While this is possible, subsequent analysis will demonstrate that complete independence is not desirable. The implementations include routines that improve run-time performance by supplying implementation-specific details.
Before considering specific techniques for implementing sets, it is worth mentioning the trade-offs one may encounter. Space and time considerations are as applicable in set algorithms as in any other area. However, the sets used in information retrieval can vary greatly in size, indeed by many orders of magnitude. Small documents, or ones being queried in the context of a particular domain, may have only a few terms. Then again, some documents will have tens of thousands of unique index terms on which users may wish to search. Sets for the former may easily be kept in memory and manipulated using fixed-space algorithms. Sets for the latter may require secondary memory implementation strategies. The same information retrieval system may well access both types of documents. One implementation approach to sets might not be enough.
In any case, large rather than small sets are likely to be the exception rather than the rule. Furthermore, the amount of information on one's system seldom shrinks. The ever-increasing amount of knowledge has made gigabyte information bases commonplace. Terabyte systems are not uncommon. Indeed, they will probably be the rule as global networks proliferate. Planning for a small, stable information base is unwise, then, and will lead to unacceptable performance. Every ounce of computing power must therefore be squeezed out of the algorithms that implement Boolean operations. The ones given here attempt to do so. They sometimes sacrifice clarity for speed, but a reader familiar with the C programming language should be able to figure them out without undue effort.
Two implementation strategies are given. This only scratches the surface of possibilities. The two approaches are sufficiently diverse as to be representative of most major trade-offs, however, and therefore will help the reader understand the benefits of other approaches he or she may come across. The technique of balanced trees is worthy of consideration; its performance is, in most respects, intermediate with respect to the approaches in this chapter. See Sedgewick (1990) for an excellent treatment of the topic.
The implementor of an information retrieval system should carefully consider the relationship of the two approaches. Certain external factors may drive which ones are practical. For instance, one technique (bit vectors) is very fast but relies on representing document names as unique integers. Doing so is certainly feasible, but--unless one's documents really are named doc1, doc2, . . .--potentially time-consuming. Whether performing the mapping for each set will result in time savings depends on the document names and the hardware available.
The desire to use this approach may also drive other design decisions in an information retrieval system. Document names are maintained in inverted indices; if the indices are sorted, the names can be mapped much more rapidly than if they are unsorted. Of course, sorting the names is an expensive operation, and practical only for precomputed indices.
This discussion illustrates the complexity that arises from a seemingly simple choice. Such decisions may influence the architecture of the entire system.
Bit vectors are a simple approach to implementing sets. They provide an extremely fast implementation that is particularly suited to sets where the element type has a small domain of possible values. The representation is not compact, as will be seen, but may be appropriate if the number of documents is small.
The approach using bit vectors is to represent a set as a sequence of bits, with one bit for each possible element in the domain of the element type. It is assumed that each value in the element's domain maps to a unique bit. If a bit's value is 1, then the element represented by that bit is in the set; if 0, the element is not in the set. These values map to the TRUE and FALSE constants of the Boolean data type, which provides a clearer understanding of the bit's purpose (TRUE means an element is in a set, FALSE means it is not) than do the digits.
Most computers do not understand bit strings of arbitrary lengths. A program must reference a minimum or maximum number of bits in a given operation--usually corresponding to a byte, word, or the like. It is therefore necessary to arrange the bit string such that it can be treated as a whole, or referenced bit-by-bit, as appropriate. The usual approach is to declare a bit string as a sequence of contiguous storage. Access to individual bits is achieved by first accessing the byte containing the desired bit(s), and then applying a "mask-and-shift" sequence (illustrated below) to recover specific bits.
The technique takes full advantage of computer hardware to achieve efficiency of operations. Most computers have instructions to perform and, or, xor, and not operations on bit strings. The C programming language, which provides access to bit-level operations, is well suited to bit vector implementations.
Consider an example. Suppose there are 20 documents, and suppose further that they may be uniquely identified by numbering them from 1 to 20, inclusive. A string of 20 bits will be used to represent sets of these documents. The first task is to determine the mapping between the numbers and bits. A logical approach is to have document i map to bit i. However, in C the first bit has index 0, not 1. Therefore, document i actually maps to bit i - 1.
Suppose a search reveals that, of the 20 documents, only documents 3, 8, 11, and 12 contain patterns of interest. The bit vector set to represent this consists of 0's at all elements except those four positions:
001000010011000000000000
The alert reader will notice that this string actually consists of 24 bits, not 20. The reason is that computers are not usually capable of storing exactly 20 bits. Most store information in multiples of 8 bits, an assumption made here. Padding the string with zeros is therefore necessary.
Suppose the system now needs to know whether document i is in the set. There is no C operation that allows bit i - 1 to be retrieved directly. However, it can be done by extracting the byte containing bit i - 1 and then setting all other bits in that byte to zero. If the resulting byte is nonzero, then bit i - 1 must have been 1; if it is zero, bit i - 1 must have been 0. The first step, then, is to compute the byte containing bit i - 1. Since there are 8 bits in a byte, each byte stores information on up to 8 elements of a set. Therefore, bit i - 1 is in byte (i - 1)/8 (as with bits, the first byte is indexed by 0, not 1).
The next step is to isolate the individual bit. Modulo arithmetic is used to do so: the bit is at location (i - 1 ) mod 8 within the byte, since the mapping scheme sequences bits in order. Shifting the bit to the first position of the byte, and then and'ing the byte with 1, yields a byte that contains 1 if the bit is 1, and 0 if the bit is 0. The complete C expression to access the bit is therefore:
The inverse operation--setting a particular bit, that is, adding an element to a set--is performed in essentially the reverse manner.
An understanding of bit-manipulation concepts makes the implementation of the remaining operations straightforward. For instance, the intersection of two sets as bit vectors is just a loop that uses C's & operation:
assuming that length (s) returns the number of bytes needed to represent set s.
The drawback of using bit vectors arises when the domain of the element type is large. Representing a set of integers on a 32-bit computer requires bit vectors of length 231/8 = 268,435,456 bytes, an amount beyond most computers' capacities. Knowing that the set will only contain a few of these elements at any time does not help. A set implemented using the above mapping still requires the full amount of space to store the two-element set containing -231 and 231 - 1. Indeed, many compilers that use bit vectors to implement sets restrict the domain to that of the maximum number of bits in a single word--typically 60 or 64. This usually limits their utility to sets of single characters.
The situation is even worse if the element type is character strings, such as might be used to hold document names. A 10-element character string restricted to upper- and lowercase letters has 5210 possible values. Clearly, bit strings will be impractical for such situations. However, there are enough small domains to warrant the consideration of bit vectors as a set implementation technique.
If large bit vectors are impractical, there must be a way to specify the domain of elements of a set. This will require adding a new function to the interface given in Figure 12.2. The function will create a new set capable of storing elements from a given range of values.
In other words, all sets will be treated as sets of integers between lower and upper, inclusive. The set operations will return sets of the same domain as their parameters, and will refuse to operate on sets of two different domains.
Since set operations need to know the domain of elements, a set will need to include information on elements. The implementation for sets, then, will contain three pieces of information: the lower and upper bounds of the set, and the bit string defining the set's elements at any time. The following structure presents this information:
This implementation rather arbitrarily restricts the maximum number of elements that a set may contain to 256. It is possible to provide more flexibility, by making bits a pointer and allocating space for it at run time, but doing so defeats the point of using bit strings for fast access--the system must worry about garbage collection issues. Such flexibility is better achieved using other representations. The implementation also defines the word size--that is, the number of bits per word in a value of type char--at 8. It is worth noting that using an int array might prove faster. Most C implementations have 8 bits in a datum of type char, and 16 or 32 in an int; using an int might make the operations that manipulate entire bytes more efficient. The decision will depend on the underlying hardware, and the types of accesses to sets that occur most frequently. Empirical analysis is the best way to resolve the question.
The implementation for Create is:
The routine simply initializes the bounds of the set. The first few lines, which deal with errors, bear explanation. As mentioned above, errors will be flagged through the use of a function Error_Occurred. This routine will be implemented as a reference to a "hidden" variable:
which would appear in the set's implementation file. Each set operation has the responsibility to set this variable to either TRUE or FALSE. The implementation of Error_Occurred is then:
Note that create does not initialize the set's contents; that is, the set is not guaranteed empty.
Since a zero indicates that an element is not in a set, and since s's bits are all zeros, set s contains no elements.
Insertion and deletion of elements are handled by setting the appropriate bit to 1 and 0, respectively. Figure 12.4 shows the code to do so. The routines mask the byte containing the appropriate bit with a bit string that turns the bit on or off, respectively. The bit string for Insert consists of a string of 0's, with a 1 at the appropriate bit; or'ing this string with a byte with result in a byte unchanged except for (possibly) the bit at the location of the 1 in the bit string. The bit string for Delete consists of a string of 1'S, with a 0 at the appropriate bit; and'ing this string with a byte will result in a byte unchanged except for (possibly) the bit at the location of the 0. C's bit-oriented operators make this simple.
The code for routines that test properties of a set was given above, in simplified form. Figure 12.5 shows the complete C routines. Note that Member is defined to be erroneous if e is not of the correct domain, that is, if it is outside the lower and upper bounds. It still returns FALSE since, as a function, it must return some value. An alternate approach would be to indicate that it is not in the set, without also flagging an error. However, this weakens the abstraction.
The Intersect, Unite and Subtract routines are next. The operations will be restricted such that all three parameters must have the same bounds. This makes the bit-vector approach simple. (Extending the operations to accommodate sets with other bounds is not difficult, but is somewhat harder for systems to use. It is left as an exercise.) Two sets thus constrained will have the same mapping function, so bit i of one set will represent the same element as bit i of another. This means that entire bytes can be combined using C's bit operators. The equivalence of two sets is tested using the macro:
Figures 12.6-12.8 show the code.
Applications sometimes need to copy sets. Using bit vectors, this is straightforward. The bits array must be copied byte by byte, since C does not permit assignment of entire arrays:
The final operation is iteration. This operation uses C's dereferencing features to execute an application-specified function. Figure 12.9 shows the code. The function f receives each element--not the bit, but the actual value. This requires converting the bit position into the value, the inverse mapping from that required for other operations. The function is expected to return a Boolean value. If this value is TRUE, another element will be passed to f; if FALSE, the iteration will cease. This lets applications exert some control over the iteration.
If a large number of documents must be searched, or if representing their names using integers is not convenient, then bit vectors are unacceptable. This section will show how to use hashing, another common set implementation technique. The approach is not as fast as bit vectors, but it makes far more efficient use of space. In fact, whereas bit vectors explicitly restrict the maximum number of elements, hashing permits sets of arbitrary size. The trade-off is in speed: performance is inversely proportional to a set's cardinality. However, good performance characteristics can be achieved if one has some idea in advance of the average size of the sets that will be manipulated, a quantity that is usually available.
Hashing is actually useful in implementing many important IR operations. Chapter 13 gives an in-depth presentation of hashing. Readers not familiar with hashing may wish to study that chapter before reading any more of this section.
The implementation will use chaining, not open addressing. It is possible, but risky, to use open addressing. A hash table must be resized when full, which is a difficult operation, as explained later.
The concepts underlying the hashing-based implementation are straightforward. Each set is implemented using a single hash table. An element is inserted in a set by inserting it into the set's hash table. Its presence is verified by examining the appropriate bucket.
This implementation will be less restrictive about typing than the implementation given for bit vectors. No assumptions will be made about the type of data; the application using the hash table will be responsible for assuring that the elements are all homogeneously typed. The results will be unpredictable if this requirement is violated. In return, it will be possible to store any type of data--not just integers. The application must provide some hints to the set operation routines about the nature of the data, however. It will supply the number of buckets and a hashing function â(v), mapping from the domain of the set elements to integers. This lets applications achieve much better performance. The information will be passed as part of the process of creating a set. There will be some enforcement of set types, however, and it will be based on this information.
The implementation of the set, then, will need to maintain this information. A plausible implementation of the set type is:
The first type definition gives the data type for set elements. Each datum is of type "char *", a C convention for a variable to contain information of any type. The second definition is used to construct the linked lists that form the buckets. The third definition contains the information needed for a set. Note that the buckets are not preallocated; only a pointer is included in the definition. The array of buckets is allocated when the set is created.
The restrictions on set equivalence can be greatly relaxed for hash sets. There are no bounds that need to be identical, as in bit vectors. The appropriate hashing function must be applied--that is, the hashing function from one table should not be used on another--but adhering to this rule is simple, since the function is included in the structure.
The creation routine is given in Figure 12.10. Note that its interface is different from the bit-vector approach, reflecting the different information needed to maintain and manipulate the sets. A "Comparator" routine must also be provided. This routine, given two values of type elementType, should return TRUE if they are equal, and FALSE if they are not. Such a routine is needed for hash tables containing strings or dynamically allocated data, since C's "= =" operator does not understand such structures.
C's global memory allocation routine, malloc, is used to provide space for the buckets. The use of dynamic memory requires some care. It must be freed when no longer needed, lest the application eventually run out of space. This will require the introduction of a "Destroy" operation, whose purpose is opposite of Create. Its implementation is left as an exercise to the reader.
In the bit-vector implementation, Create leaves the set in an uninitialized state, needing to be cleared before use. This is not feasible in hashing. The reason is that clearing the set involves freeing dynamically allocated space. In C, the presence of such storage is indicated by a non-null pointer. Therefore, Clear might become confused if Create did not set all buckets to . That, however, leaves the set "cleared." This does leave Clear able to de-allocate space:
Almost all the operations on sets will use the hashing function. Rather than repeat it in each routine, the following C macro will be used:
Insertion and deletion into a hash table involve linked-list operations. Figures 12.11 and 12.12 contain one implementation. This version of Insert ( ) inserts an element by traversing the list associated with the bucket to which it maps. If the element is not already in the list, it is inserted at the list's head. Insertion at the head is common because, in practice, elements added recently tend to be accessed most often. Data sets for which this does not hold could use an implementation where the element is added at the end of the list. Note that application-supplied hashing function is equivalent to â (v), not h (v), that is, its range is all integers rather than all integers between a certain bucket size. This simplifies dynamic resizing of hash tables (an improvement discussed in Chapter 13).
Deleting an element is done using a standard linked-list technique: the list is searched for the element while a pointer is kept to the previous node. If the element is found, the pointer to the previous node is used to make that node point to the one following the element to be deleted. The storage for the deleted node is then freed. Note that if the datum component of the node points to dynamically allocated memory, that memory will be lost unless some other node points to it. This situation may be rectified by adding a Free_datum function parameter to Create, an extension left to the reader.
Testing whether the set is empty involves testing if there are any pointers to elements. Figure 12.13 contains the code for this. It also contains the implementation of Member, done using linked-list traversal.
Constructing the union of two sets implemented using hashing is somewhat more involved than is the operation with bit vectors. No one-to-one correspondence can be established between elements. All elements that hash to the same bucket will be in the same list, but the respective lists may be ordered differently--a list's order depends on the order in which elements were inserted. The approach used is to add each element of set s1 to s3, then scan through each element of s2, adding the element to s3 if it is not already there. Figure 12.14 shows the implementation.
The concepts behind the implementations of intersection and subtraction are similar. They are shown in Figures 12.15 and 12.16. Intersecting involves traversing through s1 and adding to s3 those elements that are also in s2; subtracting works by adding to s3 those elements that are in s1 but not s2.
Copying a hash table involves copying the bucket array, plus all lists in the buckets. The code to do so is in Figure 12.17. The routine does not simply copy the lists; the data from one must be rehashed into the other, since the two may not have identical bucket array lengths or hash functions. Even if the tables are equivalent in these respects, they will not be identical after the copying operation: the order of elements within the buckets is reversed. This will only show up during iteration. Since the order of elements during iteration is not defined, the difference is irrelevant.
The final operation is iteration. It is shown in Figure 12.18. The technique to be used is similar to that of Copy: traverse through each list in each bucket, passing each datum to the function provided to Iterate. Unlike bit vectors, this traversal will almost certainly not yield the elements in any particular oder. The order will depend on both the hashing function and the order of insertion.
To aid the reader in understanding the relative merits of the two implementations, this section presents an analysis of the time and space required for the two set implementation techniques. The analysis for each is straightforward. The operations of most concern are Insert, Unite, Intersect, and Subtract, since it is presumed that most applications will spend the majority of their time manipulating sets rather than creating them. For the sake of completeness, however, all routines will be analyzed.
For bit vectors, the insertion and deletion operations are O(C), that is, their running time is constant. The exact time will depend on the speed of the division operation on the underlying hardware, the fundamental bottleneck in the implementation (bit operations such as &= and ~ are usually much quicker). The other operations, which iterate across the set, have running time that depends on the set domain. Assuming this quantity to be N, they require O(N) steps. The actual value will be closer to N/WORDSIZE, since the operations are able to access entire words rather than individual bits. The exception is Iterate( ), which must scan every bit, making it closer to O(N).
The space requirements for bit vectors are somewhat worse. They are also constant, but potentially quite large. In the implementation given here, MAX_ELEMENTS/WORDSIZE+2
The behavior of hashing algorithms is not quite so predictable. It depends on the randomness of the hashing function on the data being stored. Assuming that the hashing function is "reasonably" random, worst-case and expected behavior are not difficult to derive. Worst-case will be presented first. The hashing function is usually chosen to be O(C) (nonlinear functions defeat the advantages of hashing). The time required once the hashing function is computed will be proportional to the number of elements in the bucket. At worst, all elements will be in a single bucket. If so, then insertion, deletion, and membership tests all require O(N), where N is the number of elements in the set. The union, intersection, and difference routines have significantly poorer worst-case behavior. Consider the Unite operation on two sets that each have all elements in a single bucket. The Member() test requires O(N) steps for a single invocation. Since the inner for-loop iterates through N elements, the complexity of the loop is O(N2). This logic also applies to Intersect and Subtract.
The expected running time is significantly better. If the elements are distributed randomly, and if the number of elements N is less than the number of buckets B, then the expected number of elements in any bucket is less than one. Thus, the expected time for insertion, deletion, and membership testing would be constant, and the expected time for uniting, intersecting, or subtracting two sets would be O(N). This is likely to be a great improvement over bit vectors, since the number of elements in a set is usually very small compared to the number of elements in a domain. Of course, N cannot easily be predicted in advance, so N may very well exceed B. Even so, N must reach B2 before the performance degrades to O(N2) for union, intersection, and difference. Moreover, the number of buckets can also be increased at any time to exceed N, lowering the expected complexity to O(C). Table 12.1 summarizes this data for both approaches.
N = number of elements
C = constant
B = number of buckets in hash table
W = number of words in bit string
Hash tables require considerably less space than bit vectors. The size is determined more by the number of elements than the size of the domain. The exact formula for the space depends on the number of buckets as well. Assuming that P is the space required to store a pointer, and that each element requires E units of space, a hash table of N element requires
BP + NP + NE
units. Table 12.2 contrasts the space requirements for bit vectors and hash tables. Bytes are assumed to contain 8 bits, pointers 16. The sets are representing integers; it is assumed that the minimum possible size will be used (i.e., short, int, or long). The hash table has 503 buckets, implying that any hash table requires at least 1,006 bytes. The tables show how the advantages of bit vectors rapidly diminish in proportion to the size of the number of elements in the domain.
KERNIGHAN, B. W., and D. M. RITCHIE. 1988. The C Programming Language, 2nd ed. Englewood Cliffs, N.J.: Prentice Hall.
PARNAS, D. L. 1972. On the Criteria to be Used in Decomposing Systems into Modules. Communications of the ACM, 15(12), 1053-58.
SEDGEWICK, R. 1990. Algorithms in C. Reading, Mass: Addison-Wesley.
12.2 BOOLEAN EXPRESSIONS AND THEIR REPRESENTATION AS SETS
Find all documents that do not contain "information".
not information
Find all documents containing "information" and "retrieval".
Find all documents containing "information"
or "retrieval" (or both).
Find all documents containing "information"
or "retrieval", but not both.
Find all documents containing "information", "retrieval",
or not containing both "retrieval" and "science".
(information and retrieval) or not (retrieval and science)
 D2 is the set of all documents containing both P1 and P2 (and).
D2 is the set of all documents containing both P1 and P2 (and).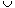 D2 is the set of all documents containing either P1 or P2 (or).
D2 is the set of all documents containing either P1 or P2 (or).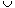 D2 - D1
D2 - D1  D2 is the set of all documents containing either P1 or P2, but not both (xor).
D2 is the set of all documents containing either P1 or P2, but not both (xor). {doc1, doc2, doc4} = {doc1}
{doc1, doc2, doc4} = {doc1}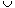 {doc1, doc2, doc4} = {doc1, doc2, doc3, doc4}
{doc1, doc2, doc4} = {doc1, doc2, doc3, doc4} {doc1, doc2, doc4})
{doc1, doc2, doc4}) 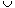 {doc1, doc2, doc3, doc4, doc5}
{doc1, doc2, doc3, doc4, doc5} {doc2, doc4, doc5})
{doc2, doc4, doc5}) {doc1, doc3, doc4, doc5}
{doc1, doc3, doc4, doc5}Document Terms
---------------------------------------------------
doc1 algorithm, information, retrieval
doc2 retrieval, science
doc3 algorithm, information, science
doc4 pattern, retrieval, science
doc5 science, algorithm
Figure 12.1: Example documents and their terms
12.3 OPERATIONS ON SETS
12.3.1 Set Interface
typedef <...> set;
typedef <...> elementType;
#define TRUE 1
#define FALSE 0
typedef int boolean;
v = "abc";
Insert(s, v);
v[1] = 'x';
Copy (s, s);
Unite(a, b, b);
void Clear(set *s); /* Make s contain zero elements. */
void Insert(set *s, /* Modify s to contain e, if */
elementType e); /* it does not already. */
void Delete(set *s, /* Remove e from s. */
elementType e);
void Unite(set *s1, set *s2, /* Make s3 the union of sets */
set *s3); /* s1 and s2. */
void Intersect(set *s1, set *s2, /* Make s3 the intersection */
set *s3); /* of sets s1 and s2. */
void Subtract(set *s1, set *s2, /* Make s3 the difference */
set *s3); /* of sets s1 and s2. */
boolean Empty(set *s); /* Return TRUE iff s has */
/* zero elements. */
boolean Member(set *s, /* Return TRUE iff e is a */
elementType e); /* member of s. */
void Copy(set *source, /* Make "destination" the */
set *destination); /* same set as "source". */
void Iterate(set *s, /* Call f(e) once for every */
boolean (*f)()); /* element e in set s. */
boolean Error_Occurred(); /* Return TRUE iff the last */
/* operation caused an error. */
Figure 12.2: Set interface operations
boolean PrintElement(i)
elementType i;
{printf("The value is %d\n", i);return TRUE;
}
Iterate(S, PrintElement);
Intersect (s1, s2, s3);
if ( Error_Occurred () ) {...
}
12.3.2 Packaging
#include "set. h"
12.3.3 Example
#include "set.h"
SolveQuery ()
{set info_docs, retr_docs, sci_docs;
set t1, t2, t3;
Clear (&info_docs);
Clear (&retr_docs);
Clear (&sci_docs);
Clear (&t1);
Clear (&t2);
Clear (&t3);
... Find the documents containing "information",
"retrieval" and "science", and put their names
into info_docs, retr_docs, and sci_docs,
respectively ...
Intersect(&info_docs, &retr_docs, &t1);
Intersect(&retr_docs, &sci_docs, &t2);
Unite(&t1, &retr_docs, &t3);
Subtract(&t3, &t2, &t1);
/* Set t1 contains the result of the query. */
}
Figure 12.3: Solving a simple set query
12.4 GENERAL CONSIDERATIONS FOR IMPLEMENTING SETS
12.5 BIT VECTORS
( vector [ (i-1) /8] >> (i-1)%8 ) & 01
for ( i = 0; i < length(s1); i++ )
s3[i] = s1[i]&s2[i];
void Create(int lower, int upper, set *s);
#define MAX_ELEMENTS 256
#define WORDSIZE 8
typedef struct {int lower;
int upper;
char bits[MAX_ELEMENTS\WORDSIZE];
} set;
void Create(lower, upper, s)
int lower, upper;
set *s;
{if ( lower > upper
|| (upper - lower) >= MAX_ELEMENTS ) {error_occurred = TRUE;
return;
}
s->lower = lower;
s->upper = upper;
error_occurred = FALSE;
}
static boolean error_occurred;
boolean Error_Occurred()
{return error_occurred;
}
void Clear(s)
set *s;
{register int i, Number_Of_Bytes;
Number_Of_Bytes = (s->upper - s-lower)/WORDSIZE + 1;
for ( i = 0; i < Number_Of_Bytes; i++ )
s->bits[i] = 0;
error_occurred = FALSE;
}
void Insert(s, e)
set *s;
elementType e;
{if ( e < s->lower || e > s->upper ) {error_occurred = TRUE;
return;
}
s->bits[(e-s->lower)/WORDSIZE] |= 01 << ( (e-s->lower)%WORDSIZE);
error_occurred = FALSE;
}
void Delete(s, e)
set *s;
elementType e;
{if ( e < s->lower || e > s->upper ) {error_occurred = TRUE;
return;
}
s->bits[(e-s->lower)/WORDSIZE] &= ~(01 << ((e-s->lower)%WORDSIZE));
error_occurred = FALSE;
}
Figure 12.4: Inserting and deleting elements in a bit-vector set
boolean Empty(s)
set *s;
{register int i, Number_Of_Bytes;
error_occurred = FALSE;
Number_Of_Bytes = (s->upper - s->lower)/WORDSIZE + 1;
for ( i = 0; i < Number_Of_Bytes; i++ )
if ( s->bits[i] )
return FALSE;
return TRUE;
}
boolean Member(s, e)
set *s;
elementType e;
{if ( error_occurred = (e < s->lower || e < s->upper) )
return FALSE;
return (s->bits[(e - s->lower)/WORDSIZE] >>
(e - s->lower)%WORDSIZE) & 01;
}
Figure 12.5: Empty and Member bit-vector routines
#define equivalent(s1, s2) \
((s1)->lower==(s2)->lower && (s1)->upper==(s2)->upper)
void Unite(s1, s2, s3)
set *s1, *s2;
set *s3;
{register int i, Number_Of_Bytes;
if ( ! (equivalent(s1, s2) && equivalent(s2, s3)) ) {error_occurred = TRUE;
return;
}
Number_Of_Bytes = (s1->upper - s1->lower)/WORDSIZE + 1;
for ( i = 0 ; i Number_Of_Bytes; i++ )
s3->bits[i] = (s1->bits[i] | s2->bits[i]);
error_occurred = FALSE;
}
Figure 12.6: Unite bit-vector routine
void Copy(source, destination)
set *source,*destination;
{register int i;
if ( ! equivalent(source, destination) ) {error_occurred = TRUE;
return;
}
for ( i = 0; i < MAX_ELEMENTS/WORDSIZE; i++ )
destination-bits[i] = source->bits[i];
error_occurred = FALSE;
}
void Intersect(s1, s2, s3)
set *s1, *s2;
set *s3;
{register int i, Number_Of_Bytes;
if ( ! (equivalent(s1, s2) && equivalent(s2, s3)) ) {error_occurred = TRUE;
return;
}
Number_Of_Bytes = (s1->upper - s1->lower)/WORDSIZE + 1;
for ( i = 0 ; i < Number_Of_Bytes; i++ )
s3->bits[i] = (s1->bits[i] & s2->bits[i]);
error_occurred = FALSE;
}
Figure 12.7: Intersect bit-vector routine
void Subtract(s1, s2, s3)
set *s1, *s2;
set *s3;
{register int i, Number_Of_Bytes;
if ( ! (equivalent(s1, s2) && equivalent(s2, s3)) ) {error_occurred = TRUE;
return;
}
Number_Of_Bytes = (s1->upper - s1->lower)/WORDSIZE + 1;
for ( i = 0 ; i < Number_Of_Bytes; i++ )
s3->bits[i] = s1->bits[i] & ~ (s2->bits[i]);
error_occurred = FALSE;
}
Figure 12.8: Subtract bit-vector routine
void Iterate(s, f)
set *s;
boolean (*f) ();
{register int i, j, Number_Of_Bytes;
Number_Of_Bytes = (s->upper - s->lower)/WORDSIZE + 1;
error_occurred = FALSE;
for ( i = 0; i < Number_Of_Bytes; i++ )
for ( j = 0; j < WORDSIZE; j++ )
if ( (s->bits[i] >> j) % 2 )
if ( ! (*f)(j + i*WORDSIZE + s->lower) )
return;
}
Figure 12.9: Bit-vector iterator routine
12.6 HASHING
typedef char element_Type;
typedef struct be_str {elementType datum;
struct be_str *next_datum;
} bucket_element;
typedef struct {int Number_Of_Buckets;
bucket_element **buckets;
int (*hashing_function)();
boolean (*comparator)();
} set;
void Create(Number_Of_Buckets, Hashing_Function, Comparator, s)
int Number_Of_Buckets;
int (*Hashing_Function)();
boolean (*Comparator)();
set *s;
{register unsigned int Bucket_Array_Size;
register int i;
if ( Number_Of_Buckets <= 0 ) {error_occurred = TRUE;
return;
}
s->Number_Of_Buckets = Number_Of_Buckets;
s->hashing_function = Hashing_Function;
s->comparator = Comparator;
Bucket_Array_Size = sizeof(bucket_element) * Number_Of_Buckets;
s->buckets = (bucket_element **)malloc(Bucket_Array_Size);
if ( error_occurred = (s->buckets == NULL) )
return;
for ( i = 0; i < Number_Of_Buckets; i++ )
s->buckets[i] = (bucket_element *)NULL;
}
Figure 12.10: Hashing version of Create
void Clear(s)
set *s;
{register int i;
register bucket_element *b, *next_b;
for ( i = 0; i < s->Number_Of_Buckets; i++ )
if ( s->buckets[i] != NULL ) {b = s->buckets[i];
while ( b != NULL ) {next_b = b->next_datum;
free( (char *)b );
b = next_b;
}
s->buckets[i] = NULL;
}
error_occurred = FALSE;
}
#define hash(s,e) (abs ((* ((s)->hashing_function)) (e)) %
(s)->Number_Of_Buckets)
void Insert(s, e)
set *s;
elementType e;
{register bucket_element *b, *New_Element;
register int bucket;
error_occurred = FALSE;
bucket = hash(s,e);
for ( b = s->buckets[bucket]; b != NULL ; b = b->next_datum )
if ( (*(s->comparator))(b->datum, e) )
return;
New_Element = (bucket_element *)malloc(sizeof (bucket_element));
if ( New_Element == NULL ) {error_occurred = TRUE;
return;
}
New_Element->datum = e;
New_Element->next_datum = s-->buckets[bucket];
s->buckets[bucket] = New_Element;
}
Figure 12.11: Inserting elements in a hash table set
void Delete(s, e)
set *s;
elementType e;
{register bucket_element *b, *previous;
register int bucket;
error_occurred = FALSE;
bucket = hash(s, e);
if ( (b = s->buckets[bucket]) == NULL )
return;
if ( (*(s->comparator))(b->datum, e) )
s->buckets[bucket] = b->next_datum;
else {while ( b->next_datum != NULL ) {if ( (*(s->comparator))(b->datum, e) )
break;
previous = b;
b = b->next_datum;
}
if ( b == NULL )
return;
previous->next_datum = b->next_datum;
}
free ( (char *)b );
}
Figure 12.12: Deleting elements from a hash table set
boolean Empty(s)
set *s;
{register int i;
error_occurred = FALSE;
for ( i = 0; i < s->Number_Of_Buckets; i++ )
if ( s->buckets[i] != NULL )
return FALSE;
return TRUE;
}
boolean Member (s, e)
set *s;
elementType e;
{register bucket_element *b;
register int bucket;
error_occurred = FALSE;
bucket = hash(s, e);
for ( b = s->buckets[bucket]; b != NULL ; b = b->next_datum )
if ( (*(s->comparator))(b->datum, e) )
return TRUE;
return FALSE;
}
Figure 12.13: Empty and Member hashing routines
void Unite(s1, s2, s3)
set *s1, *s2;
set *s3;
{register int i;
register bucket_element *b;
Copy(s1, s3);
if ( Error_Occurred() )
return;
for ( i = 0; i < s2->Number_Of_Buckets; i++ ) {if ( s2->buckets[i] == NULL )
continue;
for ( b = s2->buckets[i]; b != NULL; b = b->next_datum )
if ( ! Member(s3, b->datum) ) {Insert(s3, b->datum);
if ( Error_Occurred() )
return;
}
}
error_occurred = FALSE;
}
Figure 12.14: Unite hashing routine
void Intersect(s1, s2, s3)
set *s1, *s2;
set *s3;
{register int i;
register bucket_element *b;
Clear(s3);
for ( i = 0; i < s1->Number_Of_Buckets; i++ ) {if ( s1->buckets[i] == NULL )
continue;
for ( b = s1->buckets[i]; b != NULL; b = b->next_datum )
if ( Member(s2, b->datum) ) {Insert(s3, b->datum);
if ( Error_Occurred() )
return;
}
}
error_occurred = FALSE;
}
Figure 12.15: Intersect hashing routine
void Subtract (s1, s2, s3)
set *s1, *s2;
set *s3;
{register int i;
register bucket_element *b;
Clear(s3);
for ( i = 0; i < s1->Number_Of_Buckets; i++ ) {if ( s1->buckets[i] == NULL )
continue;
for ( b = s1->buckets[i]; b != NULL; b = b->next_datum )
if ( ! Member(s2, b->datum) ) {Insert(s3, b->datum);
if ( Error_Occurred() )
return;
}
}
error_occurred = FALSE;
}
Figure 12.16: Subtract hashing routine
12.7 ANALYSIS
void Copy(source, destination)
set *source, *destination;
{register int i h;
register bucket_element *e, *b;
Clear (destination);
for ( i = o; i < source->Number_Of_Buckets; i++ ) {if ( source->buckets[i] == NULL )
continue;
for ( b = source->buckets[i]; b != NULL; b = b->next_datum ) {h = hash(destination, b->datum);
e = (bucket_element *)malloc(sizeof (bucket_element));
if ( e == NULL ) {error_occurred = TRUE;
return;
}
e->datum = b->datum;
e->next_datum = destination->buckets[h];
destination->buckets[h] = e;
}
}
error_occurred = FALSE;
}
Figure 12.17: Copying a hash table set
void Iterate(s, f)
set *s;
boolean (*f) ();
{register int i;
register bucket_element *b;
error_occurred = FALSE;
for ( i = 0; i < s->Number_Of_Buckets; i++ )
for ( b = s->buckets[i]; b != NULL; b = b->next_datum )
if ( ! (*f) (b->datum) )
return;
}
Figure 12.18: Hashing iterator routine
 sizeof (int) bytes will be needed to store any bit-vector set. As noted previously, this can easily be rather large.
sizeof (int) bytes will be needed to store any bit-vector set. As noted previously, this can easily be rather large.Table 12.1: Relative Algorithmic Complexity for Different Set Implementations
Hashing Bit Vectors
Worst-Case Average Worst-Case Average
-------------------------------------------------------------------
Insert/Delete/Member O(N) O(C) 0(C) O(C)
Unite/Intersect/Subtract O(N2) O(N) O(W) 0(W)
Create/Empty O(B) O(B) O(W) 0(W)
Copy O(N) O(N) 0(W) 0(W)
Table 12.2: Relative Space Requirements for Different Set Implementations
Bit Vectors Hash Tables
Domain Number of Elements Domain Number of Elements
Size 64 1024 215 Size 64 1024 215
--------------------------- ----------------------------
256 32 -- -- 256 1198 4078 99,310
215 4096 4096 4096 215 1262 5102 132,078
231 228 228 228 231 1390 7100 197,614
REFERENCES


