8.1 INTRODUCTION
One technique for improving IR performance is to provide searchers with ways of finding morphological variants of search terms. If, for example, a searcher enters the term stemming as part of a query, it is likely that he or she will also be interested in such variants as stemmed and stem. We use the term conflation, meaning the act of fusing or combining, as the general term for the process of matching morphological term variants. Conflation can be either manual--using some kind of regular expressions--or automatic, via programs called stemmers. Stemming is also used in IR to reduce the size of index files. Since a single stem typically corresponds to several full terms, by storing stems instead of terms, compression factors of over 50 percent can be achieved.
As can be seen in Figure 1.2 in Chapter 1, terms can be stemmed at indexing time or at search time. The advantage of stemming at indexing time is efficiency and index file compression--since index terms are already stemmed, this operation requires no resources at search time, and the index file will be compressed as described above. The disadvantage of indexing time stemming is that information about the full terms will be lost, or additional storage will be required to store both the stemmed and unstemmed forms.
Figure 8.1 shows a taxonomy for stemming algorithms. There are four automatic approaches. Affix removal algorithms remove suffixes and/or prefixes from terms leaving a stem. These algorithms sometimes also transform the resultant stem. The name stemmer derives from this method, which is the most common. Successor variety stemmers use the frequencies of letter sequences in a body of text as the basis of stemming. The n-gram method conflates terms based on the number of digrams or n-grams they share. Terms and their corresponding stems can also be stored in a table. Stemming is then done via lookups in the table. These methods are described below.
There are several criteria for judging stemmers: correctness, retrieval effectiveness, and compression performance. There are two ways stemming can be incorrect--overstemming and understemming. When a term is overstemmed, too much of it is removed. Overstemming can cause unrelated terms to be conflated. The effect on IR performance is retrieval of nonrelevant documents. Understemming is the removal of too little of a term. Understemming will prevent related terms from being conflated. The effect of understemming on IR performance is that relevant documents will not be retrieved. Stemmers can also be judged on their retrieval effectiveness--usually measured with recall and precision as defined in Chapter 1, and on their speed, size, and so on. Finally, they can be rated on their compression performance. Stemmers for IR are not usually judged on the basis of linguistic correctness, though the stems they produce are usually very similar to root morphemes, as described below.
To illustrate how a stemmer is used in searching, consider the following example from the CATALOG system (Frakes 1984, 1986). In CATALOG, terms are stemmed at search time rather than at indexing time. CATALOG prompts for queries with the string "Look for:". At the prompt, the user types in one or more terms of interest. For example:
will cause CATALOG to attempt to find documents about system users. CATALOG takes each term in the query, and tries to determine which other terms in the database might have the same stem. If any possibly related terms are found, CATALOG presents them to the user for selection. In the case of the query term "users," for example, CATALOG might respond as follows:
The user selects the terms he or she wants by entering their numbers.
This method of using a stemmer in a search session provides a naive system user with the advantages of term conflation while requiring little knowledge of the system or of searching techniques. It also allows experienced searchers to focus their attention on other search problems. Since stemming may not always be appropriate, the stemmer can be turned off by the user. Having a user select the terms from the set found by the stemmer also reduces the likelihood of false matches.
There are several approaches to stemming. One way to do stemming is to store a table of all index terms and their stems. For example:
Terms from queries and indexes could then be stemmed via table lookup. Using a B-tree or hash table, such lookups would be very fast.
There are problems with this approach. The first is that there is no such data for English. Even if there were, many terms found in databases would not be represented, since they are domain dependent that is, not standard English. For these terms, some other stemming method would be required. Another problem is the storage overhead for such a table, though trading size for time is sometimes warranted. Storing precomputed data, as opposed to computing the data values on the fly, is useful when the computations are frequent and/or expensive. Bentley (1982), for example, reports cases such as chess computations where storing precomputed results gives significant performance improvements.
Successor variety stemmers (Hafer and Weiss 1974) are based on work in structural linguistics which attempted to determine word and morpheme boundaries based on the distribution of phonemes in a large body of utterances. The stemming method based on this work uses letters in place of phonemes, and a body of text in place of phonemically transcribed utterances.
Hafer and Weiss formally defined the technique as follows:
Let
In less formal terms, the successor variety of a string is the number of different characters that follow it in words in some body of text. Consider a body of text consisting of the following words, for example.
able, axle, accident, ape, about.
To determine the successor varieties for "apple," for example, the following process would be used. The first letter of apple is "a." "a" is followed in the text body by four characters: "b," "x," "c," and "p." Thus, the successor variety of "a" is four. The next successor variety for apple would be one, since only "e" follows "ap" in the text body, and so on.
When this process is carried out using a large body of text (Hafer and Weiss report 2,000 terms to be a stable number), the successor variety of substrings of a term will decrease as more characters are added until a segment boundary is reached. At this point, the successor variety will sharply increase. This information is used to identify stems.
Once the successor varieties for a given word have been derived, this information must be used to segment the word. Hafer and Weiss discuss four ways of doing this.
1. Using the cutoff method, some cutoff value is selected for successor varieties and a boundary is identified whenever the cutoff value is reached. The problem with this method is how to select the cutoff value--if it is too small, incorrect cuts will be made; if too large, correct cuts will be missed.
2. With the peak and plateau method, a segment break is made after a character whose successor variety exceeds that of the character immediately preceding it and the character immediately following it. This method removes the need for the cutoff value to be selected.
3. In the complete word method method, a break is made after a segment if the segment is a complete word in the corpus.
4. The entropy method takes advantage of the distribution of successor variety letters. The method works as follows. Let |D
Using this equation, a set of entropy measures can be determined for a word. A set of entropy measures for predecessors can also be defined similarly. A cutoff value is selected, and a boundary is identified whenever the cutoff value is reached.
Hafer and Weiss experimentally evaluated the various segmentation methods using two criteria: (1) the number of correct segment cuts divided by the total number of cuts, and (2) the number of correct segment cuts divided by the total number of true boundaries. They found that none of the methods performed perfectly, but that techniques that combined certain of the methods did best.
To illustrate the use of successor variety stemming, consider the example below where the task is to determine the stem of the word READABLE.
Using the complete word segmentation method, the test word "READABLE" will be segmented into "READ" and "ABLE," since READ appears as a word in the corpus. The peak and plateau method would give the same result.
After a word has been segmented, the segment to be used as the stem must be selected. Hafer and Weiss used the following rule:
The check on the number of occurrences is based on the observation that if a segment occurs in more than 12 words in the corpus, it is probably a prefix. The authors report that because of the infrequency of multiple prefixes in English, no segment beyond the second is ever selected as the stem. Using this rule in the example above, READ would be selected as the stem of READABLE.
In summary, the successor variety stemming process has three parts: (1) determine the successor varieties for a word, (2) use this information to segment the word using one of the methods above, and (3) select one of the segments as the stem. The aim of Hafer and Weiss was to develop a stemmer that required little or no human processing. They point out that while affix removal stemmers work well, they require human preparation of suffix lists and removal rules. Their stemmer requires no such preparation. The retrieval effectiveness of the Hafer and Weiss stemmer is discussed below.
Adamson and Boreham (1974) reported a method of conflating terms called the shared digram method. A digram is a pair of consecutive letters. Since trigrams, or n-grams could be used, we have called it the n-gram method. Though we call this a "stemming method," this is a bit confusing since no stem is produced.
In this approach, association measures are calculated between pairs of terms based on shared unique digrams. For example, the terms statistics and statistical can be broken into digrams as follows.
Thus, "statistics" has nine digrams, seven of which are unique, and "statistical" has ten digrams, eight of which are unique. The two words share six unique digrams: at, ic, is, st, ta, ti.
Once the unique digrams for the word pair have been identified and counted, a similarity measure based on them is computed. The similarity measure used was Dice's coefficient, which is defined as
where A is the number of unique digrams in the first word, B the number of unique digrams in the second, and C the number of unique digrams shared by A and B. For the example above, Dice's coefficient would equal (2 x 6)/(7 + 8) = .80. Such similarity measures are determined for all pairs of terms in the database, forming a similarity matrix. Since Dice's coefficient is symmetric (Sij = Sji), a lower triangular similarity matrix can be used as in the example below.
Once such a similarity matrix is available, terms are clustered using a single link clustering method as described in Chapter 16. The algorithm for calculating a digram similarity matrix follows.
When they used their method on a sample of words from Chemical Titles, Adamson and Boreham found that most pairwise similarity measures were 0. Thus, the similarity matrix will be sparse, and techniques for handling sparse matrices will be appropriate. Using a cutoff similarity value of .6, they found ten of the eleven clusters formed were correct. More significantly, in hardly any cases did the method form false associations. The authors also report using this method successfully to cluster document titles.
Affix removal algorithms remove suffixes and/or prefixes from terms leaving a stem. These algorithms sometimes also transform the resultant stem. A simple example of an affix removal stemmer is one that removes the plurals from terms. A set of rules for such a stemmer is as follows (Harman 1991).
In this algorithm only the first applicable rule is used.
Most stemmers currently in use are iterative longest match stemmers, a kind of affix removal stemmer first developed by Lovins (1968). An iterative longest match stemmer removes the longest possible string of characters from a word according to a set of rules. This process is repeated until no more characters can be removed. Even after all characters have been removed, stems may not be correctly conflated. The word "skies," for example, may have been reduced to the stem "ski" which will not match "sky." There are two techniques to handle this--recoding or partial matching.
Recoding is a context sensitive transformation of the form AxC -> AyC where A and C specify the context of the transformation, x is the input string, and y is the transformed string. We might, for example, specify that if a stem ends in an "i" following a "k," then i -> y. In partial matching, only the n initial characters of stems are used in comparing them. Using this approach, we might say that two stems are equivalent if they agree in all but their last characters.
In addition to Lovins, iterative longest match stemmers have been reported by Salton (1968), Dawson (1974), Porter (1980), and Paice (1990). As discussed below, the Porter algorithm is more compact than Lovins, Salton, and Dawson, and seems, on the basis of experimentation, to give retrieval performance comparable to the larger algorithms. The Paice stemmer is also compact, but since experimental data was not available for the Paice algorithm, we chose the Porter algorithm as the example of this type of stemmer.
The Porter algorithm consists of a set of condition/action rules. The conditions fall into three classes: conditions on the stem, conditions on the suffix, and conditions on the rules.
There are several types of stem conditions.
1. The measure, denoted m, of a stem is based on its alternate vowel-consonant sequences. Vowels are a, e, i, o, u, and y if preceded by a consonant. Consonants are all letters that are not vowels. Let C stand for a sequence of consonants, and V for a sequence of vowels. The measure m, then, is defined as
[C](VC)m[V]
The superscript m in the equation, which is the measure, indicates the number of VC sequences. Square brackets indicate an optional occurrence. Some examples of measures for terms follows.
2. * < X >--the stem ends with a given letter X
3. *v*--the stem contains a vowel
4. *d--the stem ends in a double consonant
5. *o--the stem ends with a consonant-vowel-consonant, sequence, where the final consonant is not w, x, or y.
Suffix conditions take the form: (current_suffix == pattern). Rule conditions take the form: (rule was used).
Actions are rewrite rules of the form:
old_suffix -> new_suffix
The rules are divided into steps. The rules in a step are examined in sequence, and only one rule from a step can apply. The longest possible suffix is always removed because of the ordering of the rules within a step. The algorithm is as follows.
The rules for the steps of the stemmer are as follows.
A full implementation of this stemmer, in C, is in the appendix to this chapter.
There have been many experimental evaluations of stemmers. Salton (1968) examined the relative retrieval performance of fully stemmed terms against terms with only the suffix "s" removed. The stemmer used was an iterative longest match stemmer of the type described above, employing about 200 endings. Three document collections were used in these studies: the IRE-3 collection consisting of 780 computer science abstracts and 34 search requests, the ADI collection consisting of 82 papers and 35 search requests, and the Cranfield-1 collection consisting of 200 aerodynamics abstracts and 42 search requests.
Differences between the two conflation methods, fully stemmed and "s" stemmed, were calculated on 14 dependent variables for each query: rank recall, log precision, normalized recall, normalized precision, and precision for ten recall levels. As Salton points out, these measures are probably intercorrelated, and since the inferential tests used require independence of the dependent variables, the results reported must be viewed with caution. This data was analyzed using both related group t tests and sign tests. Both of these statistical methods yielded significant results at the .05 probability level, but since none of the t values are reported, precluding their use in an estimate of effect size, and since sufficient data is provided for the estimate of effect size from the sign tests, the latter will be discussed here. (The effect size is the percentage of the variance of the independent variable accounted for by the dependent variables.) The effect size for a sign test is the difference between the obtained proportion (that is, the number of cases favoring a given method over the number of all cases where a difference was detected), and the expected proportion if there is no difference between means (that is, .50*).
*The effect size for a sign test can only take on values in the range 0 to .5.
For the IRE-3 collection, 476 differences were used for the sign test (the 14 dependent variables measures
The most striking feature of these experiments is the discrepancy between the results for the IRE-3 and ADI collections, and the results for the Cranfield-1 collection. Salton offers the plausible explanation that the discrepancy is due to the highly technical and homogenous nature of the Cranfield vocabulary. He states:
To be able to differentiate between the various document abstracts, it is . . . important to maintain finer distinctions for the Cranfield case than for ADI and IRE, and these finer distinctions are lost when several words are combined into a unique class through the suffix cutoff process.
One of Salton's assertions about these experiments seems ill founded in light of the effect sizes calculated above. He states that, "For none of the collections (ADI, IRE-3, Cranfield-1) is the improvement of one method over the other really dramatic, so that in practice, either procedure might reasonably be used" . It seems much more reasonable, given the differences observed between the methods, to conclude that conflation may have a significant effect on retrieval performance, but that the effect may depend on the vocabulary involved. It may be, however, that Salton's remarks are based on unreported t-test data which may have indicated small effect sizes. The sign test is insensitive to the magnitude of differences, and thus a large effect might be found using a sign test, while a small effect was found using a t-test.
Hafer and Weiss (1974) tested their stemmer against other stemming methods using the ADI collection, and the Carolina Population Center (CPC) Collection consisting of 75 documents and five queries. Comparisons were made on the basis of recall-precision plots. No statistical testing was reported. For the ADI collection, the Hafer and Weiss stemmer outperformed the SMART stemmer. The authors also determined "each family derived from a common stem . . . by hand." . The method and criteria used are not reported. In a test using the CRC collection, the Hafer and Weiss stemmer performed equally to the manually derived stems. All methods of stemming outperformed full terms for both test collections.
Van Rijsbergen et al. (1980) tested their stemmer (Porter 1980) against the stemmer described by Dawson (1974) using the Cranfield-1 test collection. Both of these stemmers are of the longest match type, though the Dawson stemmer is more complex. They report that the performance of their stemmer was slightly better across ten paired recall-precision levels, but that the observed differences are probably not meaningful. No statistical results of any kind are reported.
Katzer et al. (1982) examined the performance of stemmed title-abstract terms against six other document representations: unstemmed title-abstract terms, unstemmed abstract terms, unstemmed title terms, descriptors, identifiers, and descriptors and identifiers combined. The stemmer used was a simple suffix removal stemmer employing 20 endings.
The database consisted of approximately 12,000 documents from Computer and Control Abstracts. Seven experienced searchers were used in the study, with each searcher searching different representations for each query. Relevance judgments on a scale of 1-4 (highly relevant to nonrelevant) were obtained from the users who requested the searches.
The dependent variable measures used were recall and precision for highly relevant documents, and recall and precision for all documents. On no dependent variable did stemmed terms perform less well than other representations, and in some cases they performed significantly better than descriptors, and on all document recall, stemming did significantly better than both descriptors and title terms. The effect sizes, calculated here on the basis of reported data, were .26 for highly relevant, and .22 and .20 for all relevant. The results of this study must be viewed with some caution because for a given query, different searchers searched different representations. This means that observed differences between representations may to some degree have been caused by searcher-representation interactions.
Lennon et al. (1981) examined the performance of various stemmers both in terms of retrieval effectiveness and inverted file compression. For the retrieval comparisons, the Cranfield-1400 collection was used. This collection contains 1,396 documents, and also 225 queries. The titles of documents and the queries were matched, and the documents ranked in order of decreasing match value. A cutoff was then applied to specify a given number of the highest ranked documents. This procedure was done for each of the methods used, that is, eight stemming methods, and nonstemmed terms.
The evaluation measure was E, as defined in Chapter 1. The various methods were evaluated at b levels of .5 (indicating that a user was twice as interested in precision as recall), and 2 (indicating that a user was twice as interested in recall as precision). These levels of b were not chosen by users, but were set by the experimenters.
The eight stemmers used in this study were: the Lovins stemmer, the Porter stemmer, the RADCOL stemmer, a suffix frequency stemmer based on the RADCOL project, a stemmer developed by INSPEC, the Hafer and Weiss stemmer, a trigram stemmer, and a stemmer based on the frequency of word endings in a corpus. As stated above, unstemmed terms were also used.
Thus, the two questions that this study addressed concerned (1) the relative effectiveness of stemming versus nonstemming, and (2) the relative performance of the various stemmers examined. In terms of the first question, only the Hafer and Weiss stemmer did worse than unstemmed terms at the two levels of b. At the b = .5 level, the INSPEC, Lovins, Porter, trigram, and both frequency stemmers all did better than unstemmed terms, and at the b = 2 level, all but Hafer and Weiss did better than unstemmed terms.
This information was derived from a table of means reported for the two b levels. As for the second question, though Lennon et al. (1981) report that, "a few of the differences between algorithms were statistically significant at the .05 probability level of significance in the precision oriented searches" , they fail to report any test statistics or effect sizes, or even identify which pairs of methods were significantly different. They conclude that
Despite the very different means by which the various algorithms have been developed, there is relatively little difference in terms of the dictionary compression and retrieval performance obtained from their use; in particular, simple, fully automated methods perform as well as procedures which involve a large degree of manual involvement in their development.
This assertion seems to be contradicted by the significant differences found between algorithms. However, the paucity of reported data in this study makes an independent evaluation of the results extremely difficult.
Frakes (1982) did two studies of stemming. The first tested the hypothesis that the closeness of stems to root morphemes will predict improved retrieval effectiveness. Fifty-three search queries were solicited from users and searched by four professional searchers under four representations: title, abstract, descriptors, and identifiers. The experiments were done using a database of approximately 12,000 document representations from six months of psychological abstracts. The retrieval system used was DIATOM (Waldstein 1981), a DIALOG simulator. In addition to most of the features of DIALOG, DIATOM allows stemmed searching using Lovins' (1968) algorithm, and permits search histories to be trapped and saved into files. As is the case with almost all IR systems, DIATOM allows only right and internal truncation; thus, the experiments did not address prefix removal.
User need statements were solicited from members of the Syracuse University academic community and other institutions. Each user need statement was searched by four experienced searchers under four different representations (abstract, title, identifiers, and descriptors). Each searcher did a different search for each representation. In addition, some user statements were searched using a stemmed title-abstract representation. This study made use of only title and abstract searches, since searches of these fields were most likely to need conflation, together with stemmed searches. However, relevant documents retrieved under all representations were used in the calculation of recall measures.
The hypothesis for the first experiment, based on linguistic theory, was that terms truncated on the right at the root morpheme boundary will perform better than terms truncated on the right at other points. To test this hypothesis, searches based on 34 user need statements were analyzed using multiple regression, and the non-parametric Spearman's test for correlation. The independent variables were positive and negative deviations of truncation points from root boundaries, where deviation was measured in characters. Root morphemes were determined by applying a set of generation rules to searcher supplied full-term equivalents of truncated terms, and checking the results against the linguistic intuitions of two judges.
The dependent variables were E measures (see Chapter 1) at three trade-off values: b = .5 ( precision twice as important as recall), b = 1 (precision equals recall in importance), b = 2 ( recall twice as important as precision). The data analysis showed that searchers truncated at or near the root morpheme boundaries. The mean number of characters that terms truncated by searchers varied from root boundaries in a positive direction was .825 with a standard deviation of .429. Deviations in a negative direction were even smaller with a mean of .035 and a standard deviation of .089. The tests of correlation revealed no significant relationship between the small deviations of stems from root boundaries, and retrieval effectiveness.
The purpose of the second experiment was to determine if conflation can be automated with no loss of retrieval effectiveness. Smith (1979), in an extensive survey of artificial intelligence techniques for information retrieval, stated that "the application of truncation to content terms cannot be done automatically to duplicate the use of truncation by intermediaries because any single rule [used by the conflation algorithm] has numerous exceptions" ( p. 223). However, no empirical test of the relative effectiveness of automatic and manual conflation had been made. The hypothesis adopted for the second experiment was that stemming will perform as well or better than manual conflation.
To test this hypothesis, searches based on 25 user need statements were analyzed. The primary independent variable was conflation method--with the levels automatic (stemming) and manual. The blocking variable was queries, and searchers was included as an additional independent variable to increase statistical power. Data was derived by re-executing each search with stemmed terms in place of the manually conflated terms in the original searches. The dependent variables were E measures at the three trade-off levels as described above. No significant difference was found between manual and automatic conflation, indicating that conflation can be automated with no significant loss in retrieval performance.
Walker and Jones (1987) did a thorough review and study of stemming algorithms. They used Porter's stemming algorithm in the study. The database used was an on-line book catalog (called RCL) in a library. One of their findings was that since weak stemming, defined as step 1 of the Porter algorithm, gave less compression, stemming weakness could be defined by the amount of compression. They also found that stemming significantly increases recall, and that weak stemming does not significantly decrease precision, but strong stemming does. They recommend that weak stemming be used automatically, with strong stemming reserved for those cases where weak stemming finds no documents. Another finding was that the number of searches per session was about the same for weak and strong stemming.
Harman (1991) used three stemmers--Porter, Lovins, and S removal--on three databases--Cranfield 1400, Medlars, and CACM--and found that none of them significantly improved retrieval effectiveness in a ranking IR system called IRX. The dependent variable measure was again E, at b levels of .5, 1.0, and 2.0. Attempts to improve stemming performance by reweighting stemmed terms, and by stemming only shorter queries, failed in this study.
Table 8.1 summarizes the various studies of stemming for improving retrieval effectiveness.
These studies must be viewed with caution. The failure of some of the authors to report test statistics, especially effect sizes, make interpretation difficult. Since some of the studies used sample sizes as small as 5 (Hafer and Weiss), their validity is questionable. Given these cautions, we offer the following conclusions.
Since a stem is usually shorter than the words to which it corresponds, storing stems instead of full words can decrease the size of index files. Lennon et al. (1981), for example, report the following compression percentages for various stemmers and databases. For example, the indexing file for the Cranfield collection was 32.1 percent smaller after it was stemmed using the INSPEC stemmer.
It is obvious from this table that the savings in storage using stemming can be substantial.
Harman (1991) reports that for a database of 1.6 megabytes of source text, the index was reduced 20 percent, from .47 megabytes to .38 megabytes, using the Lovins stemmer. For larger databases, however, reductions are smaller. For a database of 50 megabytes, the index was reduced from 6.7 to 5.8 megabytes--a savings of 13.5 percent. She points out, however, that for real world databases that contain numbers, misspellings, proper names, and the like, the compression factors are not nearly so large.
Compression rates increase for affix removal stemmers as the number of suffixes increases, as the following table, also from the Lennon et al. study, shows.
Stemmers are used to conflate terms to improve retrieval effectiveness and/or to reduce the size of indexing files. Stemming will, in general, increase recall at the cost of decreased precision. Studies of the effects of stemming on retrieval effectiveness are equivocal, but in general stemming has either no effect, or a positive effect, on retrieval performance where the measures used include both recall and precision. Stemming can have a marked effect on the size of indexing files, sometimes decreasing the size of the files as much as 50 percent.
Several approaches to stemming were described--table lookup, affix removal, successor variety, and n-gram. The Porter stemmer was described in detail, and a full implementation of it, in C, is presented in the appendix to this chapter. In the next chapter, the thesaurus approach to conflating semantically related words is discussed.
ADAMSON, G., and J. BOREHAM. 1974. "The Use of an Association Measure Based on Character Structure to Identify Semantically Related Pairs of Words and Document Titles," Information Storage and Retrieval, 10, 253-60.
BENTLEY, J. 1982. Writing Efficient Programs. Englewood Cliffs, N.J.: Prentice Hall.
DAWSON, J. 1974. "Suffix Removal and Word Conflation." ALLC Bulletin, Michelmas, 33-46.
FRAKES, W. B. 1982. Term Conflation for Information Retrieval, Doctoral Dissertation, Syracuse University.
FRAKES, W. B. 1984. "Term Conflation for Information Retrieval" in Research and Development in Information Retrieval, ed. C. van Rijsbergen. New York: Cambridge University Press.
FRAKES, W. B. 1986. "LATTIS: A Corporate Library and Information System for the UNIX Environment," Proceedings of the National Online Meeting, Medford, N.J.: Learned Information Inc., 137-42.
HAFER, M., and S. WEISS. 1974. "Word Segmentation by Letter Successor Varieties," Information Storage and Retrieval, 10, 371-85.
HARMAN, D. 1991. "How Effective is Suffixing?" Journal of the American Society for Information Science, 42(1), 7-15.
KATZER, J., M. MCGILL, J. TESSIER, W. FRAKES, and P. DAS GUPTA. 1982. "A Study of the Overlaps among Document Representations," Information Technology: Research and Development, 1, 261-73.
LENNON, M., D. PIERCE, B. TARRY, and P. WILLETT. 1981. "An Evaluation of Some Conflation Algorithms for Information Retrieval." Journal of Information Science 3, 177-83.
LOVINS, J. B. 1968. "Development of a Stemming Algorithm." Mechanical Translation and Computational Linguistics, 11(1-2), 22-31.
PAICE, C. 1990. "Another Stemmer," ACM SIGIR Forum, 24(3), 56-61.
PORTER, M. F. 1980. "An Algorithm for Suffix Stripping." Program, 14(3), 130-37.
SALTON, G. 1968. Automatic Information Organization and Retrieval. New York: McGraw-Hill.
SMITH, L. C. 1979. Selected Artificial Intelligence Techniques in Information Retrieval. Doctoral Dissertation, Syracuse University.
VAN RIJSBERGEN, C. J., S. E. ROBERTSON, and M. F. PORTER. 1980. New Models in Probabilistic Information Retrieval. Cambridge: British Library Research and Development Report no. 5587.
WALKER, S., and R. JONES. 1987. "Improving Subject Retrieval in Online Catalogues." British Library Research Paper no. 24, vol. 1.
WALDSTEIN, R. 1981. "Diatom: A Dialog Simulator." Online, 5, 68-72.
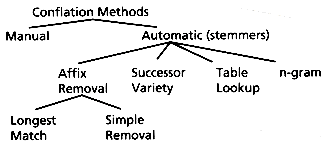
Figure 8.1: Conflation methods
8.1.1 Example of Stemmer Use in Searching
Look for: system users
Search Term: users
Term Occurrences
1. user 15
2. users 1
3. used 3
4. using 2
Which terms (0 = none, CR = all):
8.2 TYPES OF STEMMING ALGORITHMS
Term Stem
---------------------
engineering engineer
engineered engineer
engineer engineer
8.2.1 Successor Variety
 be a word of length n;
be a word of length n;  i, is a length i prefix of
i, is a length i prefix of  . Let D be the corpus of words. D
. Let D be the corpus of words. D i is defined as the subset of D containing those terms whose first i letters match
i is defined as the subset of D containing those terms whose first i letters match  i exactly. The successor variety of
i exactly. The successor variety of  i, denoted S
i, denoted S i, is then defined as the number of distinct letters that occupy the i + 1st position of words in D
i, is then defined as the number of distinct letters that occupy the i + 1st position of words in D i. A test word of length n has n successor varieties S
i. A test word of length n has n successor varieties S i, S
i, S 2, . . . , S
2, . . . , S n.
n.  i| be the number of words in a text body beginning with the i length sequence of letters
i| be the number of words in a text body beginning with the i length sequence of letters  . Let |D
. Let |D ij| be the number of words in D
ij| be the number of words in D i with the successor j. The probability that a member of D
i with the successor j. The probability that a member of D i has the successor j is given by
i has the successor j is given by 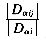 . The entropy of |D
. The entropy of |D i| is
i| is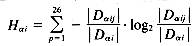
Test Word: READABLE
Corpus: ABLE, APE, BEATABLE, FIXABLE, READ, READABLE
READING, READS, RED, ROPE, RIPE.
Prefix Successor Variety Letters
-----------------------------------------
R 3 E,I,O
RE 2 A,D
REA 1 D
READ 3 A,I,S
READA 1 B
READAB 1 L
READABL 1 E
READABLE 1 BLANK
if (first segment occurs in <= 12 words in corpus)
first segment is stem
else (second segment is stem)
8.2.2 n-gram stemmers
statistics => st ta at ti is st ti ic cs
unique digrams = at cs ic is st ta ti
statistical => st ta at ti is st ti ic ca al
unique digrams = al at ca ic is st ta ti
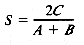
word1 word2 word3. . .wordn-1
word1
word2 S21
word3 S31 S32


wordn Sn1 Sn2 Sn3 Sn(n-1)
/* calculate similarity matrix for words based on digrams */
#define MAXGRAMS 50 /* maximum n-grams for a word */
#define GRAMSIZE 2 /* size of the n-gram */
void
digram_smatrix (wordlist, word_list_length, smatrix)
char *wordlist[]; /* list of sorted unique words */
int word_list_length; /* length of wordlist */
double *smatrix[];
{int i, j; /* loop counters */
int uniq_in_wordl; /* number of unique digrams in word 1 */
int uniq_in_word2; /* number of unique digrams in word 2 */
int common_uniq; /* number of unique digrams shared by words 1 and 2 */
char uniq_digrams_1 [MAXGRAMS] [GRAMSIZE]; /* array of digrams */
char uniq_digrams_2 [MAXGRAMS] [GRAMSIZE]; /* array of digrams */
int unique_digrams(); /* function to calculate # of unique digrams in word */
int common_digrams(); /* function to calculate # of shared unique digrams */
for ( i=0; i< word_list_length; ++i)
for (j=i+1; j <word_list_length ;++j) {/* find unique digrams for first word in pair */
uniq_in_word1 = unique_digrams(wordlist [i], uniq_digrams 1);
/* find unique digrams for second word in pair */
uniq_in_word2 = unique_digrams(wordlist [j], uniq_digrams_2);
/* find number of common unique digrams */
common_uniq = common_digrams(uniq_digrams_1, uniq_digrams_2);
/* calculate similarity value and store in similarity matrix */
smatrix[i][j] = (2*common_uniq)/(uniq_in_word1+uniq_in_word2);
} /* end for */
} /* end digram_smatrix */
8.2.3 Affix Removal Stemmers
If a word ends in "ies" but not "eies" or "aies"
Then "ies" -> "y"
If a word ends in "es" but not "aes", "ees", or "oes"
then "es" -> "e"
If a word ends in "s", but not "us" or "ss"
then "s" -> NULL
Measure Examples
---------------------------------------
m=0 TR, EE, TREE, Y, BY
m=1 TROUBLE, OATS, TREES, IVY
m=2 TROUBLES, PRIVATE, OATEN
{step1a(word);
step1b(stem);
if (the second or third rule of step 1b was used)
step1b1(stem);
step1c(stem);
step2(stem);
step3(stem);
step4(stem);
step5a(stem);
step5b(stem);
}
Step 1a Rules
Conditions Suffix Replacement Examples
---------------------------------------------------
NULL sses ss caresses -> caress
NULL ies i ponies -> poni
ties -> tie
NULL ss ss carress -> carress
NULL s NULL cats -> cat
Step 1b Rules
Conditions Suffix Replacement Examples
----------------------------------------------------
(m>0) eed ee feed-> feed
agreed -> agree
(*v*) ed NULL plastered-> plaster
bled -> bled
(*v*) ing NULL motoring-> motor
sing-> sing
Step 1b1 Rules
Conditions Suffix Replacement Examples
------------------------------------------------------------------------
NULL at ate conflat(ed) -> conflate
NULL bl ble troubl(ing) -> trouble
NULL iz ize siz(ed) -> size
(*d and not
(*<L> or *<S> or *<Z>)) NULL single letter hopp(ing) -> hop
tann(ed) -> tan
fall(ing) -> fall
hiss(ing) -> hiss
fizz(ed) -> fizz
(m=1 and *o) NULL e fail(ing) -> fail
fil(ing) -> file
Step 1c Rules
Conditions Suffix Replacement Examples
-----------------------------------------------------------
(*v*) y i happy - > happi
sky -> sky
Step 2 Rules
Conditions Suffix Replacement Examples
--------------------------------------------------------------
(m>0) ational ate relational -> relate
(m>0) tional tion conditional -> condition
rational -> rational
(m>0) enci ence valenci -> valence
(m>0) anci ance hesitanci -> hesitance
(m>0) izer ize digitizer -> digitize
(m>0) abli able conformabli -> conformable
(m>0) alli al radicalli -> radical
(m>0) entli ent differentli -> different
(m>0) eli e vileli -> vile
(m>0) ousli ous analogousli -> analogous
(m>0) ization ize vietnamization -> vietnamize
(m>0) ation ate predication -> predicate
(m>0) ator ate operator -> operate
(m>0) alism al feudalism -> feudal
(m>0) iveness ive decisiveness -> decisive
(m>0) fulness ful hopefulness -> hopeful
(m>0) ousness ous callousness -> callous
(m>0) aliti al formaliti -> formal
(m>0) iviti ive sensitiviti -> sensitive
(m>0) biliti ble sensibiliti -> sensible
Step 3 Rules
Conditions Suffix Replacement Examples
--------------------------------------------------------
(m>0) icate ic triplicate -> triplic
(m>0) ative NULL formative -> form
(m>0) alize al formalize -> formal
(m>0) iciti ic electriciti -> electric
(m>0) ical ic electrical -> electric
(m>0) ful NULL hopeful -> hope
(m>0) ness NULL goodness -> good
Step 4 Rules
Conditions Suffix Replacement Examples
---------------------------------------------------------------------
(m>1) al NULL revival -> reviv
(m>1) ance NULL allowance -> allow
(m>1) ence NULL inference -> infer
(m>1) er NULL airliner-> airlin
(m>1) ic NULL gyroscopic -> gyroscop
(m>1) able NULL adjustable -> adjust
(m>1) ible NULL defensible -> defens
(m>1) ant NULL irritant -> irrit
(m>1) ement NULL replacement -> replac
(m>1) ment NULL adjustment -> adjust
(m>1) ent NULL dependent -> depend
(m>1 and (*<S> or *<T>)) ion NULL adoption -> adopt
(m>1) ou NULL homologou-> homolog
(m>1) ism NULL communism-> commun
(m>1) ate NULL activate -> activ
(m>1) iti NULL angulariti -> angular
(m>1) ous NULL homologous -> homolog
(m>1) ive NULL effective -> effect
(m>1) ize NULL bowdlerize -> bowdler
Step 5a Rules
Conditions Suffix Replacement Examples
---------------------------------------------------------
(m>1) e NULL probate -> probat
rate - > rate
(m=1 and not *o) e NULL cease - > ceas
Step 5b Rules
Conditions Suffix Replacement Examples
-------------------------------------------------------------------
(m> 1 and *d and *<L>) NULL single letter controll -> control
roll -> roll
8.3 EXPERIMENTAL EVALUATIONS OF STEMMING
 34 queries). Of these, 272 pairs favored full stemming, 132 pairs favored suffix "s" stemming, and in 72 cases neither method was favored. Thus, the effect size for the IRE-3 collection is 272/ (272+132) - .50 = .175. In the test of ADI collection, 254 cases were found to favor full stemming, 107 cases favored suffix "s" stemming, and 129 cases favored neither. The effect size for this collection is .20. The results for the Cranfield-1 collection are opposite those for IRE-3 and ADI. For Cranfield-1, 134 cases favored full stemming, 371 favored the suffix "s" stemming, and 183 favored neither. The effect size for this collection is .235.
34 queries). Of these, 272 pairs favored full stemming, 132 pairs favored suffix "s" stemming, and in 72 cases neither method was favored. Thus, the effect size for the IRE-3 collection is 272/ (272+132) - .50 = .175. In the test of ADI collection, 254 cases were found to favor full stemming, 107 cases favored suffix "s" stemming, and 129 cases favored neither. The effect size for this collection is .20. The results for the Cranfield-1 collection are opposite those for IRE-3 and ADI. For Cranfield-1, 134 cases favored full stemming, 371 favored the suffix "s" stemming, and 183 favored neither. The effect size for this collection is .235.8.3.1 Stemming Studies: Conclusion
 Stemming can affect retrieval performance, but the studies are equivocal. Where effects have been found, the majority have been positive, with the Hafer and Weiss stemmer in the study by Lennon et al., and the effect of the strong stemmer in the Walker and Jones study, being the exceptions. Otherwise there is no evidence that stemming will degrade retrieval effectiveness.
Stemming can affect retrieval performance, but the studies are equivocal. Where effects have been found, the majority have been positive, with the Hafer and Weiss stemmer in the study by Lennon et al., and the effect of the strong stemmer in the Walker and Jones study, being the exceptions. Otherwise there is no evidence that stemming will degrade retrieval effectiveness. Stemming is as effective as manual conflation.
Stemming is as effective as manual conflation. Salton's results indicate that the effect of stemming is dependent on the nature of the vocabulary used. A specific and homogeneous vocabulary may exhibit different conflation properties than will other types of vocabularies.
Salton's results indicate that the effect of stemming is dependent on the nature of the vocabulary used. A specific and homogeneous vocabulary may exhibit different conflation properties than will other types of vocabularies. There also appears to be little difference between the retrieval effectiveness of different full stemmers, with the exception of the Hafer and Weiss stemmer, which gave poorer performance in the Lennon et al. study.
There also appears to be little difference between the retrieval effectiveness of different full stemmers, with the exception of the Hafer and Weiss stemmer, which gave poorer performance in the Lennon et al. study.Table 8.1: Stemming Retrieval Effectiveness Studies Summary
Study Question Test Collection Dependent Vars Results
-----------------------------------------------------------------------
Salton Full stemmer IRE-3 14 DV's Full > s
vs.
suffix s ADI Full > s
stemmer
Cranfield-1 s > Full
-----------------------------------------------------------------------
Hafer and HW stemmer ADI recall(R), HW > SMART
Weiss vs.
SMART precision (P)
stemmer
HW stemmer CRC HW=Manual
vs.
manual
stemming
stemmed vs. ADI Stemmed >
unstemmed CRC Unstemmed
-----------------------------------------------------------------------
VanRijs- Porter vs. Cranfield-1 R,P Porter =
bergen Dawson Dawson
et al. stemmer
-----------------------------------------------------------------------
Katzer stemmed vs. CCA R,P(highest) stemmed =
et al. unstemmed 12,000 R,P(all) unstemmed
stemmed vs. stemmed >
other reps. title,
descriptors
-----------------------------------------------------------------------
Lennon stemmed vs. Cranfield-1400 E(.5,2) stemmed >
et al. unstemmed unstemmed >
HW stemmer
stemmer stemmers =
comparison
-----------------------------------------------------------------------
Frakes closeness Psychabs E(.5,1,2) No
of stem to improvement
root morpheme
improves IR
performance
truncation truncation=
vs. stemming stemming
-----------------------------------------------------------------------
Walker stemmed vs. PCL R stemmed >
and Jones unstemmed unstemmed
weak stemmed PCL P weak stemmed=
vs. unstemmed unstemmed
strong stemmed PCL P strong
vs. unstemmed stemmed <
unstemmed
-----------------------------------------------------------------------
Harman stemmed vs. Cranfield-1400 E(.5,1,2) stemmed =
unstemmed unstemmed
Medlars
CACM " "
" "
8.4 STEMMING TO COMPRESS INVERTED FILES
Index Compression Percentages from Stemming
Stemmer Cranfield National Physical Laboratory INSPEC Brown Corpus
----------------------------------------------------------------------
INSPEC 32.1 40.7 40.5 47.5
Lovins 30.9 39.2 39.5 45.8
RADCOL 32.1 41.8 41.8 49.1
Porter 26.2 34.6 33.8 38.8
Frequency 30.7 39.9 40.1 50.5
Compression vs. Suffix Set Size: NPL Database
------------------------------------------------------------------
Number of Suffixes 100 200 300 400 500 600 700 800
Compression 28.2 33.7 35.9 37.3 38.9 40.1 41.0 41.6
8.5 SUMMARY
REFERENCES
APPENDIX
/******************************* stem.c **********************************
Version: 1.1
Purpose: Implementation of the Porter stemming algorithm.
Provenance: Written by C. Fox, 1990.
Notes: This program is a rewrite of earlier versions by B. Frakes and S. Cox
**/
/************************ Standard Include Files *************************/
#include <stdio.h>
#include <string.h>
#include <ctype.h>
/******************** Private Function Declarations **********************/
static int WordSize( /* word */ );
static int ContainsVowel( /* word */ );
static int EndsWithCVC( /* word */ );
static int AddAnE( /* word */ );
static int RemoveAnE( /* word */ );
static int ReplaceEnd( /* word, rule */ );
/***************** Private Defines and Data Structures *******************/
#define FALSE 0
#define TRUE 1
#define EOS '\0'
#define IsVowel(c) ('a' == (c) | | 'e' == (c) | | 'i' == (c) | | 'o' == (c) | | 'u' == (c))typedef struct {int id; /* returned if rule fired */
char *old_end; /* suffix replaced */
char *new_end; /* suffix replacement */
int old_offset; /* from end of word to start of suffix */
int new_offset; /* from beginning to end of new suffix */
int min_root_size; /* min root word size for replacement */
int (*condition)(); /* the replacement test function */
} RuleList;
static char LAMBDA[1] = " "; /* the constant empty string */
static char *end; /* pointer to the end of the word */
static RuleList step1a_rules[] =
{101, "sses", "ss", 3, 1, -1, NULL,
102, "ies", "i", 2, 0, -1, NULL,
103, "ss", "ss", 1, 1, -1, NULL,
104, "s", LAMBDA, 0, -1, -1, NULL,
000, NULL, NULL, 0, 0, 0, NULL,
};
static RuleList step1b_rules[] =
{105, "eed", "ee", 2, 1, 0, NULL,
106, "ed", LAMBDA, 1, -1, -1, ContainsVowel,
107, "ing", LAMBDA, 2, -1, -1, ContainsVowel,
000, NULL, NULL, 0, 0, 0, NULL,
};
static RuleList step1b1_rules[ ] =
{108, "at", "ate", 1, 2, -1, NULL,
109, "bl", "ble", 1, 2, -1, NULL,
110, "iz", "ize", 1, 2, -1, NULL,
111, "bb" "b", 1, 0, -1, NULL,
112, "dd" "d", 1, 0, -1, NULL,
113, "ff", "f", 1, 0, -1, NULL,
114, "gg", "g", 1, 0, -1, NULL,
115, "mm, "m", 1, 0, -1, NULL,
116, "nn", "n", 1, 0, -1, NULL,
117, "pp", "p", 1, 0, -1, NULL,
118, "rr", "r", 1, 0, -1, NULL,
119, "tt", "t", 1, 0, -1, NULL,
120, "ww", "w", 1, 0, -1, NULL,
121, "xx", "x", 1, 0, -1, NULL,
122, LAMBDA "e", -1, 0, -1, AddAnE,
000, NULL, NULL, 0, 0, 0, NULL,
} ;
static RuleList step1c_rules[ ] =
{123, "y", "i", 0, 0, -1, ContainsVowel,
000, NULL, NULL, 0, 0, 0, NULL,
};
static RuleList step2_rules[ ] =
{203, "ational", "ate", 6, 2, 0, NULL,
204, "tional", "tion", 5, 3, 0, NULL,
205, "enci", "ence", 3, 3, 0, NULL,
206, "anci", "ance", 3, 3, 0, NULL,
207, "izer", "ize", 3, 2, 0, NULL,
208, "abli", "able", 3, 3, 0, NULL,
209, "alli", "al", 3, 1, 0, NULL,
210, "entli", "ent", 4, 2, 0, NULL,
211, "eli", "e", 2, 0, 0, NULL,
213, "ousli", "ous", 4, 2, 0, NULL,
214, "ization", "ize", 6, 2, 0, NULL,
215, "ation", "ate", 4, 2, 0, NULL,
216, "ator", "ate", 3, 2, 0, NULL,
217, "alism", "al", 4, 1, 0, NULL,
218, "iveness", "ive", 6, 2, 0, NULL,
219, "fulnes", "ful", 5, 2, 0, NULL,
220, "ousness", "ous", 6, 2, 0, NULL,
221, "aliti", "al", 4, 1, 0, NULL,
222, "iviti", "ive", 4, 2, 0, NULL,
223, "biliti", "ble", 5, 2, 0, NULL,
000, NULL, NULL, 0, 0, 0, NULL,
};
static RuleList step3_rules[ ] =
{301, "icate", "ic", 4, 1, 0, NULL,
302, "ative", LAMBDA, 4, -1, 0, NULL,
303, alize", "al", 4, 1, 0, NULL,
304, "iciti", "ic", 4, 1, 0, NULL,
305, "ical", "ic", 3, 1, 0, NULL,
308, "ful", LAMBDA, 2, -1, 0, NULL,
309, "ness", LAMBDA, 3, -1, 0, NULL,
000, NULL, NULL, 0, 0, 0, NULL,
};
static RuleList step4_rules[ ] =
{401, "al", LAMBDA, 1, -1, 1, NULL,
402, "ance", LAMBDA, 3, -1, 1, NULL,
403, "ence", LAMBDA, 3, -1, 1, NULL,
405, "er", LAMBDA, 1, -1, 1, NULL,
406, "ic", LAMBDA, 1, -1, 1, NULL,
407, "able", LAMBDA, 3, -1, 1, NULL,
408, "ible", LAMBDA, 3, -1, 1, NULL,
409, "ant", LAMBDA, 2, -1, 1, NULL,
410, "ement", LAMBDA, 4, -1, 1, NULL,
411, "ment", LAMBDA, 3, -1, 1, NULL,
412, "ent", LAMBDA, 2, -1, 1, NULL,
423, "sion", "s", 3, 0, 1, NULL,
424, "tion", "t", 3, 0, 1, NULL,
415, "ou", LAMBDA, 1, -1, 1, NULL,
416, "ism", LAMBDA, 2, -1, 1, NULL,
417, "ate", LAMBDA, 2, -1, 1, NULL,
418, "iti", LAMBDA, 2, -1, 1, NULL,
419, "ous", LAMBDA, 2, -1, 1, NULL,
420, "ive", LAMBDA, 2, -1, 1, NULL,
421, "ize", LAMBDA, 2, -1, 1, NULL,
000, NULL, NULL, 0, 0, 0, NULL,
};
static RuleList step5a_rules[ ] =
{501, "e", LAMBDA, 0, -1, 1, NULL,
502, "e", LAMBDA, 0, -1, -1, RemoveAnE,
000, NULL, NULL, 0, 0, 0, NULL,
};
static RuleList step5b_rules[ ] =
{503, "ll", "l", 1, 0, 1, NULL,
000, NULL, NULL, 0, 0, 0, NULL,
};
/*******************************************************************/
/******************** Private Function Declarations **************/
/*FN****************************************************************
WordSize( word )
Returns: int -- a weird WordSize of word size in adjusted syllables
Purpose: Count syllables in a special way: count the number
vowel-consonant pairs in a word, disregarding initial
consonants and final vowels. The letter "y" counts as a
consonant at the beginning of a word and when it has a vowel
in front of it; otherwise (when it follows a consonant) it
is treated as a vowel. For example, the WordSize of "cat"
is 1, of "any" is 1, of "amount" is 2, of "anything" is 3.
Plan: Run a DFA to compute the word size
Notes: The easiest and fastest way to compute this funny measure is
with a finite state machine. The initial state 0 checks
the first letter. If it is a vowel, then the machine changes
to state 1, which is the "last letter was a vowel" state.
If the first letter is a consonant or y, then it changes
to state 2, the "last letter was a consonant state". In
state 1, a y is treated as a consonant (since it follows
a vowel), but in state 2, y is treated as a vowel (since
it follows a consonant. The result counter is incremented
on the transition from state 1 to state 2, since this
transition only occurs after a vowel-consonant pair, which
is what we are counting.
**/
static int
WordSize( word )
register char *word; /* in: word having its WordSize taken */
{register int result; /* WordSize of the word */
register int state; /* current state in machine */
result = 0;
state = 0;
/* Run a DFA to computer the word size */
while ( EOS != *word )
{switch ( state )
{case 0: state = (IsVowel(*word)) ? 1: 2;
break;
case 1: state = (IsVowel(*word)) ? 1 : 2;
if ( 2 == state ) result++;
break;
case 2: state = (IsVowel(*word) | | ('y' == *word)) ? 1 : 2;break;
}
word++;
}
return( result );
} /* WordSize */
/*FN************************************************************************
ContainsVowel( word )
Returns: int -- TRUE (1) if the word parameter contains a vowel,
FALSE (0) otherwise.
Purpose: Some of the rewrite rules apply only to a root containing
a vowel, where a vowel is one of "aeiou" or y with a
consonant in front of it.
Plan: Obviously, under the definition of a vowel, a word contains
a vowel iff either its first letter is one of "aeiou", or
any of its other letters are "aeiouy". The plan is to
test this condition.
Notes: None
**/
static int
ContainsVowel( word )
register char *word; /* in: buffer with word checked */
{if ( EOS == *word )
return( FALSE );
else
return ( IsVowel(*word) | | (NULL != strpbrk(word+1,"aeiouy")) );
} /* ContainsVowel */
/*FN**********************************************************************
EndsWithCVC( word )
Returns: int -- TRUE (1) if the current word ends with a
consonant-vowel-consonant combination, and the second
consonant is not w, x, or y, FALSE (0) otherwise.
Purpose: Some of the rewrite rules apply only to a root with
this characteristic.
Plan: Look at the last three characters.
Notes: None
**/
static int
EndsWithCVC( word )
register char *word; /* in: buffer with the word checked */
{int length; /* for finding the last three characters */
if ( (length = strlen(word)) < 2 )
return( FALSE );
else
{end = word + length - 1;
return( (NULL == strchr("aeiouwxy", *end--)) /* consonant */&& (NULL != strchr("aeiouy", *end--)) /* vowel */&& (NULL == strchr("aeiou", *end )) ) /* consonant */}
} /* EndsWithCVC */
/*FN***********************************************************************
AddAnE( word )
Returns: int -- TRUE (1) if the current word meets special conditions
for adding an e.
Purpose: Rule 122 applies only to a root with this characteristic.
Plan: Check for size of 1 and a consonant-vowel-consonant ending.
Notes: None
**/
static int
AddAnE( word )
register char *word;
{return( (1 == WordSize(word)) && EndsWithCVC(word) );
} /* AddAnE */
/*FN************************************************************************
RemoveAnE( word )
Returns: int -- TRUE (1) if the current word meets special conditions
for removing an e.
Purpose: Rule 502 applies only to a root with this characteristic.
Plan: Check for size of 1 and no consonant-vowel-consonant ending.
Notes: None
**/
static int
RemoveAnE( word )
register char *word;
{return( (1 == WordSize(word)) && !EndsWithCVC(word) );
} /* RemoveAnE */
/*FN************************************************************************
ReplaceEnd( word, rule )
Returns: int -- the id for the rule fired, 0 is none is fired
Purpose: Apply a set of rules to replace the suffix of a word
Plan: Loop through the rule set until a match meeting all conditions
is found. If a rule fires, return its id, otherwise return 0.
Connditions on the length of the root are checked as part of this
function's processing because this check is so often made.
Notes: This is the main routine driving the stemmer. It goes through
a set of suffix replacement rules looking for a match on the
current suffix. When it finds one, if the root of the word
is long enough, and it meets whatever other conditions are
required, then the suffix is replaced, and the function returns.
**/
static int
ReplaceEnd( word, rule )
register char *word; /* in/out: buffer with the stemmed word */
RuleList *rule; /* in: data structure with replacement rules */
{register char *ending; /* set to start of possible stemmed suffix */
char tmp_ch; /* save replaced character when testing */
while ( 0 != rule->id )
{ending = end - rule->old_offset;
if ( word = ending )
if ( 0 == strcmp(ending,rule->old_end) )
{tmp_ch = *ending;
*ending = EOS;
if ( rule->min_root_size < WordSize(word) )
if ( !rule->condition | | (*rule->condition)(word) )
{(void)strcat( word, rule->new_end );
end = ending + rule->new_offset;
break;
}
*ending = tmp_ch;
}
rule++;
}
return( rule->id );
} /* ReplaceEnd */
/************************************************************************/
/********************* Public Function Declarations ********************/
/*FN************************************************************************
Stem( word )
Returns: int -- FALSE (0) if the word contains non-alphabetic characters
and hence is not stemmed, TRUE (1) otherwise
Purpose: Stem a word
Plan: Part 1: Check to ensure the word is all alphabetic
Part 2: Run through the Porter algorithm
Part 3: Return an indication of successful stemming
Notes: This function implements the Porter stemming algorithm, with
a few additions here and there. See:
Porter, M.F., "An Algorithm For Suffix Stripping,"
Program 14 (3), July 1980, pp. 130-137.
Porter's algorithm is an ad hoc set of rewrite rules with
various conditions on rule firing. The terminology of
"step 1a" and so on, is taken directly from Porter's
article, which unfortunately gives almost no justification
for the various steps. Thus this function more or less
faithfully refects the opaque presentation in the article.
Changes from the article amount to a few additions to the
rewrite rules; these are marked in the RuleList data
structures with comments.
**/
int
Stem( word )
register char *word; /* in/out: the word stemmed */
{int rule; /* which rule is fired in replacing an end */
/* Part 1: Check to ensure the word is all alphabetic */
for ( end = word; *end != EOS; end++ )
if ( !isalpha(*end) ) return( FALSE );
end--;
/* Part 2: Run through the Porter algorithm */
ReplaceEnd( word, step1a_rules );
rule = ReplaceEnd( word, step1b_rules );
if ( (106 == rule) | | (107 == rule) )
ReplaceEnd( word, step1b1_rules );
ReplaceEnd( word, step1c_rules );
ReplaceEnd( word, step2_rules );
ReplaceEnd( word, step3_rules );
ReplaceEnd( word, step4_rules );
ReplaceEnd( word, step5a_rules );
ReplaceEnd( word, step5b_rules );
/* Part 3: Return an indication of successful stemming */
return( TRUE );
} /* Stem */


