University of Maryland, College Park and UMIACS
Abstract
This chapter presents a survey and discussion on signature-based text retrieval methods. It describes the main idea behind the signature approach and its advantages over other text retrieval methods, it provides a classification of the signature methods that have appeared in the literature, it describes the main representatives of each class, together with the relative advantages and drawbacks, and it gives a list of applications as well as commercial or university prototypes that use the signature approach.
Text retrieval methods have attracted much interest recently (Christodoulakis et al. 1986; Gonnet 1982; Gonnet and Tompa 1987; Stanfill and Kahle 1986; Tsichritzis and Christodoulakis 1983). There are numerous applications involving storage and retrieval of textual data:
The main operational characteristics of all the above applications are the following two:
Test retrieval methods form the following large classes (Faloutsos 1985): Full text scanning, inversion, and signature files, on which we shall focus next.
Signature files are based on the idea of the inexact filter: They provide a quick test, which discards many of the nonqualifying items. The qualifying items definitely pass the test; some additional items ("false hits" or "false drops") may also pass it accidentally. The signature file approach works as follows: The documents are stored sequentially in the "text file." Their "signatures" (hash-coded bit patterns) are stored in the "signature file." When a query arrives, the signature file is scanned and many nonqualifying documents are discarded. The rest are either checked (so that the "false drops" are discarded) or they are returned to the user as they are.
A brief, qualitative comparison of the signature-based methods versus their competitors is as follows: The signature-based methods are much faster than full text scanning (1 or 2 orders of magnitude faster, depending on the individual method). Compared to inversion, they require a modest space overhead (typically
On the other hand, signature files may be slow for large databases, precisely because their response time is linear on the number of items N in the database. Thus, signature files have been used in the following environments:
1. PC-based, medium size db
2. WORMs
3. parallel machines
4. distributed text db
This chapter is organized as follows: In section 4.2 we present the basic concepts in signature files and superimposed coding. In section 4.3 we discuss methods based on compression. In section 4.4 we discuss methods based on vertical partitioning of the signature file. In section 4.5 we discuss methods that use both vertical partitioning and compression. In section 4.6 we present methods that are based on horizontal partitioning of the signature file. In section 4.7 we give the conclusions.
Signature files typically use superimposed coding (Moders 1949) to create the signature of a document. A brief description of the method follows; more details are in Faloutsos (1985). For performance reasons, which will be explained later, each document is divided into "logical blocks," that is, pieces of text that contain a constant number D of distinct, noncommon words. (To improve the space overhead, a stoplist of common words is maintainted.) Each such word yields a "word signature," which is a bit pattern of size F, with m bits set to "1", while the rest are "0" (see Figure 4.1). F and m are design parameters. The word signatures are OR'ed together to form the block signature. Block signatures are concatenated, to form the document signature. The m bit positions to be set to "1" by each word are decided by hash functions. Searching for a word is handled by creating the signature of the word and by examining each block signature for "1" 's in those bit positions that the signature of the search word has a "1".
In order to allow searching for parts of words, the following method has been suggested (Faloutsos and Christodoulakis 1984): Each word is divided into successive, overlapping triplets (e.g., "fr", "fre", "ree", "ee" for the word "free"). Each such triplet is hashed to a bit position by applying a hashing function on a numerical encoding of the triplet, for example, considering the triplet as a base-26 number. In the case of a word that has l triplets, with l > m, the word is allowed to set l (nondistinct) bits. If l < m, the additional bits are set using a random number generator, initialized with a numerical encoding of the word.
An important concept in signature files is the false drop probability Fd. Intuitively, it gives the probability that the signature test will fail, creating a "false alarm" (or "false hit" or "false drop"). Notice that the signature test never gives a false dismissal.
DEFINITION: False drop probability, Fd, is the probability that a block signature seems to qualify, given that the block does not actually qualify. Expressed mathematically:
The signature file is an F
This is the reason that documents have to be divided into logical blocks: Without logical blocks, a long document would have a signature full of "l" 's, and it would always create a false drop. To avoid unnecessary complications, for the rest of the discussion we assume that all the documents span exactly one logical block.
The most straightforward way to store the signature matrix is to store the rows sequentially. For the rest of this work, the above method will be called SSF, for Sequential Signature File. Figure 4.2 illustrates the file structure used: In addition to the text file and the signature file, we need the so-called "pointer file," with pointers to the beginnings of the logical blocks (or, alternatively, to the beginning of the documents).
Although SSF has been used as is, it may be slow for large databases. Many methods have been suggested, trying to improve the response time of SSF, trading off space or insertion simplicity for speed. The main ideas behind all these methods are the following:
1. Compression: If the signature matrix is deliberately sparse, it can be compressed.
2. Vertical partitioning: Storing the signature matrix columnwise improves the response time on the expense of insertion time.
3. Horizontal partitioning: Grouping similar signatures together and/or providing an index on the signature matrix may result in better-than-linear search.
The methods we shall examine form the classes shown in Figure 4.3. For each of these classes we shall describe the main idea, the main representatives, and the available performance results, discussing mainly
In this section we examine a family of methods suggested in Faloutsos and Christodoulakis (1987). These methods create sparse document signatures on purpose, and then compress them before storing them sequentially. Analysis in that paper showed that, whenever compression is applied, the best value for m is 1. Also, it was shown that the resulting methods achieve better false drop probability than SSF for the same space overhead.
The idea in these methods is that we use a (large) bit vector of B bits and we hash each word into one (or perhaps more, say n) bit position(s), which are set to "1" (see Figure 4.4). The resulting bit vector will be sparse and therefore it can be compressed.
The spacewise best compression method is based on run-length encoding (McIlroy 1982), using the approach of "infinite Huffman codes" (Golomb 1966; Gallager and van Voorhis 1975). However, searching becomes slow. To determine whether a bit is "1" in the sparse vector, the encoded lengths of all the preceding intervals (runs) have to be decoded and summed (see Figure 4.5).
This method accelerates the search by sacrificing some space, compared to the run-length encoding technique. The compression method is based on bit-blocks, and was called BC (for bit-Block Compression). To speed up the searching, the sparse vector is divided into groups of consecutive bits (bit-blocks); each bit-block is encoded individually. The size of the bit-blocks is chosen according to Eq. (A2.2) in Faloutsos and Christodoulakis (1987) to achieve good compression. For each bit-block we create a signature, which is of variable length and consists of at most three parts (see Figure 4.6):
Part I. It is one bit long and it indicates whether there are any "l"s in the bit-block (1) or the bit-block is empty (0). In the latter case, the bit-block signature stops here.
Part II. It indicates the number s of "1"s in the bit-block. It consists of s - 1 "1"s and a terminating zero. This is not the optimal way to record the number of "1"s. However this representation is simple and it seems to give results close to the optimal. [See Eq. (4.1.4, 4.1.5) in Faloutsos and Christodoulakis (1987)].
Part III. It contains the offsets of the "1"s from the beginning of the bit-block (1 gb bits for each "1", where b is the bit-block size).
Figure 4.6 illustrates how the BC method compresses the sparse vector of Figure 4.4. Figure 4.7 illustrates the way to store parts of a document signature: the first parts of all the bit-block signatures are stored consecutively, then the second parts, and so on.
The BC method was slightly modified to become insensitive to changes in the number of words D per block. This is desirable because the need to split messages in logical blocks is eliminated, thus simplifying the resolution of complex queries: There is no need to "remember" whether some of the terms of the query have appeared in one of the previous logical blocks of the message under inspection.
The idea is to use a different value for the bit-block size bopt for each message, according to the number W of bits set to "1" in the sparse vector. The size of the sparse vector B is the same for all messages. Analysis in Faloutsos and Christodoulakis (1987) shows how to choose the optimal size b of the bit-blocks for a document with W (distinct) words; arithmetic examples in the same paper indicate the advantages of the modified method.
This method was called VBC (for Variable bit-Block Compression). Figure 4.8 illustrates an example layout of the signatures in the VBC method. The upper row corresponds to a small message with small W, while the lower row to a message with large W. Thus, the upper row has a larger value of bopt, fewer bit-blocks, shorter Part I (the size of Part I is the number of bit-blocks), shorter Part II (its size is W) and fewer but larger offsets in Part III (the size of each offset is log bopt bits).
With respect to space overhead, the two methods (BC and VBC) require less space than SSF for the same false drop probability. Their response time is slightly less than SSF, due to the decreased I/0 requirements. The required main-memory operations are more complicated (decompression, etc.), but they are probably not the bottleneck. VBC achieves significant savings even on main-memory operations. With respect to insertions, the two methods are almost as easy as the SSF; they require a few additional CPU cycles to do the compression.
As shown in Figure 4.9, the BC method achieves
The idea behind the vertical partitioning is to avoid bringing useless portions of the document signature in main memory; this can be achieved by storing the signature file in a bit-sliced form (Roberts 1979; Faloutsos and Chan 1988) or in a "frame-sliced" form (Lin and Faloutsos 1988).
The bit-sliced design is illustrated in Figure 4.10.
To allow insertions, we propose using F different files, one per each bit position, which will be referred to as "bit-files." The method will be called BSSF, for "Bit-Sliced Signature Files." Figure 4.11 illustrates the proposed file structure.
Searching for a single word requires the retrieval of m bit vectors (instead of all of the F bit vectors) which are subsequently ANDed together. The resulting bit vector has N bits, with "1" 's at the positions of the qualifying logical blocks.
An insertion of a new logical block requires F disk accesses, one for each bit-file, but no rewriting! Thus, the proposed method is applicable on WORM optical disks. As mentioned in the introduction, commercial optical disks do not allow a single bit to be written; thus, we have to use a magnetic disk, that will hold the last page of each file; when they become full, we will dump them on the optical disk. The size of each bit file can be predicted (Faloutsos and Chan 1988) and the appropriate space can be preallocated on the disk.
The following data are taken from product specification:
Micropolis,
Alcatel Thompson Gigadisk GM 1001 (WORM) Seek time within +/- 100 tracks = 35 ms; Seek time beyond current band = 200 ms; Latency (avg) = 27 ms; Transfer rate = 3.83 Mbits/sec; Sector size = 1K bytes.
The traditional design of BSSF suggests chosing the optimal value for m to be such that the document signatures contain "l"s by 50 percent. A typical value of m is of the order of 10 (Christodoulakis and Faloutsos 1984). This implies 10 random disk accesses on a single word query. In Lin and Faloutsos (1988) it is suggested to use a smaller than optimal value of m; thus, the number of random disk accesses decreases. The drawback is that, in order to maintain the same false drop probability, the document signatures have to be longer.
The idea behind this method (Lin and Faloutsos 1988) is to force each word to hash into bit positions that are close to each other in the document signature.Then, these bit files are stored together and can be retrieved with few random disk accesses. The main motivation for this organization is that random disk accesses are more expensive than sequential ones, since they involve movement of the disk arm.
More specifically, the method works as follows: The document signature (F bits long) is divided into k frames of s consecutive bits each. For each word in the document, one of the k frames will be chosen by a hash function; using another hash function, the word sets m bits (not necessarily distinct) in that frame. F, k, s, m are design parameters. Figure 4.12 gives an example for this method.
The signature matrix is stored framewise. Each frame will be kept in consecutive disk blocks. Only one frame has to be retrieved for a single word query, that is, only one random disk access is required. At most, n frames have to be scanned for an n word query. Insertion will be much faster than BSSF since we need only access k frames instead of F bit-slices. This method will be referred to as Frame-Sliced Signature file (FSSF).
In FSSF, each word selects only one frame and sets m bit positions in that frame. A more general approach is to select n distinct frames and set m bits (not necessarily distinct) in each frame to generate the word signature. The document signature is the OR-ing of all the word signatures of all the words in that document. This method is called Generalized Frame-Sliced Signature File (GFSSF; Lin and Faloutsos 1988).
Notice that BSSF, B'SSF, FSSF, and SSF are actually special cases of GFSSF:
Since GFSSF is a generalized model, we expect that a careful choice of the parameters will give a method that is better (whatever the criterion is) than any of its special cases. Analysis in the above paper gives formulas for the false drop probability and the expected response time for GFSSF and the rest of the methods. Figure 4.13 plots the theoretically expected performance of GFSSF, BSSF, B'SSF, and FSSF. Notice that GFSSF is faster than BSSF, B'SSF, and FSSF, which are all its special cases. It is assumed that the transfer time for a page
Ttrans = 1 msec
and the combined seek and latency time Tseek is
Tseek = 40 msec
The text file was 2.8Mb long, with average document size
The experiments were conducted on a SUN 3/50 with a local disk, when the load was light; the system was implemented in C, under UNIX. The experiments on the 2.8Mb database showed good agreement between the theoretical and experimental values for the false drop probability. The maximum relative error was 16 percent. The average response time ("real time") was 420 ms for FSSF with s = 63, m = 8, Ov = 18 percent, and 480 ms for GFSSF with s = 15, n = 3, m = 3, and Ov = 18 percent.
The idea in all the methods in this class (Faloutsos and Chan 1988) is to create a very sparse signature matrix, to store it in a bit-sliced form, and compress each bit slice by storing the position of the "1"s in the slice. The methods in this class are closely related to inversion with a hash table.
Although the bit-sliced method is much faster than SSF on retrieval, there may be room for two improvements:
1. On searching, each search word requires the retrieval of m bit files, exactly because each word signature has m bits set to "1". The search time could be improved if m was forced to be "1".
2. The insertion of a logical block requires too many disk accesses (namely, F, which is typically 600-1,000).
If we force m = l, then F has to be increased, in order to maintain the same false drop probability (see the formulas in Faloutsos and Chan [1988]. For the next three methods, we shall use S to denote the size of a signature, to highlight the similarity of these methods to inversion using hash tables. The corresponding bit matrix and bit files will be sparse and they can be compressed. Figure 4.14 illustrate a sparse bit matrix. The easiest way to compress each bit file is to store the positions of the "1" 's. However, the size of each bit file is unpredictable now, subject to statistical variations. Therefore, we store them in buckets of size Bp, which is a design parameter. As a bit file grows, more buckets are allocated to it on demand. These buckets are linked together with pointers. Obviously, we also need a directory (hash table) with S pointers, one for each bit slice. Notice the following:
1. There is no need to split documents into logical blocks any more.
2. The pointer file can be eliminated. Instead of storing the position of each "1" in a (compressed) bit file, we can store a pointer to the document in the text file.
Thus, the compressed bit files will contain pointers to the appropriate documents (or logical blocks). The set of all the compressed bit files will be called "leve1 1" or "postings file," to agree with the terminology of inverted files (Salton and McGill 1983).
The postings file consists of postings buckets, of size Bp bytes (Bp is a design parameter). Each such bucket contains pointers to the documents in the text file, as well as an extra pointer, to point to an overflow postings bucket, if necessary.
Figure 4.15 illustrates the proposed file structure, and gives an example, assuming that the word "base" hashes to the 30-th position (h("base") = 30), and that it appears in the document starting at the 1145-th byte of the text file.
Searching is done by hashing a word to obtain the postings bucket address. This bucket, as well as its overflow buckets, will be retrieved, to obtain the pointers to the relevant documents. To reduce the false drops, the hash table should be sparse. The method is similar to hashing. The differences are the following:
a. The directory (hash table) is sparse; Traditional hashing schemes require loads of 80-90 percent.
b. The actual word is stored nowhere. Since the hash table is sparse, there will be few collisions. Thus, we save space and maintain a simple file structure.
The motivation behind this method is to try to compress the sparse directory of CBS. The file structure we propose consists of a hash table, an intermediate file, a postings file and the text file as in Figure 4.16. The method is similar to CBS. It uses a hashing function h1(), which returns values in the range (O,(S-1)) and determines the slot in the directory. The difference is that DCBS makes an effort to distinguish among synonyms, by using a second hashing function h2(), which returns bit strings that are h bits long. These hash codes are stored in the "intermediate file," which consists of buckets of Bi bytes (design parameter). Each such bucket contains records of the form (hashcode, ptr). The pointer ptr is the head of a linked list of postings buckets.
Figure 4.16 illustrates an example, where the word "base" appears in the document that starts at the 1145-th byte of the text file. The example also assumes that h = 3 bits, hl("base") = 30, and h2("base") = (011)2.
Searching for the word "base" is handled as follows:
Step 1 h1("base") = 30: The 30-th pointer of the directory will be followed. The corresponding chain of intermediate buckets will be examined.
Step 2 h2("base") = (011)2: The records in the above intermediate buckets will be examined. If a matching hash code is found (at most one will exist!), the corresponding pointer is followed, to retrieve the chain of postings buckets.
Step 3 The pointers of the above postings buckets will be followed, to retrieve the qualifying (actually or falsely) documents.
Insertion is omitted for brevity.
This method avoids false drops completely, without storing the actual words in the index. The idea is to modify the intermediate file of the DCBS, and store a pointer to the word in the text file. Specifically, each record of the intermediate file will have the format (hashcode, ptr, ptr-to-word), where ptr-to-word is a pointer to the word in the text file. See Figure 4.17 for an illustration.
This way each word can be completely distinguished from its synonyms, using only h bits for the hash code and p (=4 bytes, usually) for the ptr-to-word. The advantages of storing ptr-to-word instead of storing the actual word are two: (1) space is saved (a word from the dictionary is
Searching is done in a similar way with DCBS. The only difference is that, whenever a matching hash code is found in Step 2, the corresponding ptr-to-word is followed, to avoid synonyms completely.
In Faloutsos and Chan (1988), an analytical model is developed for the performance of each of the above methods. Experiments on the 2.8Mb database showed that the model is accurate. Figure 4.18 plots the theoretical performance of the methods (search time as a function of the overhead).
The final conclusion is that these methods are fast, requiring few disk accesses, they introduce 20-25 percent space overhead, and they still require append-only operations on insertion.
The motivation behind all these methods is to avoid the sequential scanning of the signature file (or its bit-slices), in order to achieve better than O(N) search time. Thus, they group the signatures into sets, partitioning the signature matrix horizontally. The grouping criterion can be decided beforehand, in the form of a hashing function h(S), where S is a document signature (data independent case). Alternatively, the groups can be determined on the fly, using a hierarchical structure (e.g. a B-tree--data dependent case).
The earliest approach was proposed by Gustafson (1971). Suppose that we have records with, say six attributes each. For example, records can be documents and attributes can be keywords describing the document. Consider a hashing function h that hashes a keyword w to a number h(w) in the range 0-15. The signature of a keyword is a string of 16 bits, all of which are zero except for the bit at position h(w). The record signature is created by superimposing the corresponding keyword signatures. If k < 6 bits are set in a record signature, additional 6 - k bits are set by some random method. Thus, there are comb (16,6) = 8,008 possible distinct record signatures (where C(m,n) denotes the combinations of m choose n items). Using a hash table with 8,008 slots, we can map each record signature to one such slot as follows: Let p1 < p2 < . . . < p6 the positions where the "1"s occur in the record signature. Then the function
maps each distinct record signature to a number in the range 0-8,007. The interesting point of the method is that the extent of the search decreases quickly (almost exponentially) with the number of terms in the (conjunctive) query. Single word queries touch C(15,5) = 3,003 slots of the hash table, two-word queries touch C(14, 4) = 1,001 slots, and so on.
Although elegant, Gustafson's method suffers from some practical problems:
1. Its performance deteriorates as the file grows.
2. If the number of keywords per document is large, then either we must have a huge hash table or usual queries (involving 3-4 keywords) will touch a large portion of the database.
3. Queries other than conjunctive ones are handled with difficulty.
Lee and Leng (1989) proposed a family of methods that can be applied for longer documents. They suggested using a portion of a document signature as a signature key to partition the signature file. For example, we can choose the first 20 bits of a signature as its key and all signatures with the same key will be grouped into a so-called "module." When a query signature arrives, we will first examine its signature key and look for the corresponding modules, then scan all the signatures within those modules that have been selected. They report 15 to 85 percent speedups over SSF, depending on the number of bits being specified in the query signature.
Sacks-Davis and his colleagues (1983, 1987) suggested using two levels of signatures. Their documents are bibliographic records of variable length. The first level of signatures consists of document signatures that are stored sequentially, as in the SSF method. The second level consists of "block signatures"; each such signature corresponds to one block (group) of bibliographic records, and is created by superimposing the signatures of all the words in this block, ignoring the record boundaries. The second level is stored in a bit-sliced form. Each level has its own hashing functions that map words to bit positions.
Searching is performed by scanning the block signatures first, and then concentrating on these portions of the first-level signature file that seem promising.
Analysis on a database with N
A subtle problem arises when multiterm conjunctive queries are asked, (e.g., "data and retrieval"): A block may result in an unsuccessful block match, because it may contain the desired terms, but not within the same record. The authors propose a variety of clever ways to minimize these block matches.
Deppisch (1986) proposed a B-tree like structure to facilitate fast access to the records (which are signatures) in a signature file. The leaf of an S-tree consists of k "similar" (i.e., with small Hamming distance) document signatures along with the document identifiers. The OR-ing or these k document signatures forms the "key" of an entry in an upper level node, which serves as a directory for the leaves. Recursively we construct directories on lower level directories until we reach the root. The S-tree is kept balanced in a similar manner as a B-trees: when a leaf node overflows it is split in two groups of "similar" signatures; the father node is changed appropriately to reflect the new situation. Splits may propagate upward until reaching the root.
The method requires small space overhead; the response time on queries is difficult to estimate analytically. The insertion requires a few disk accesses (proportional to the height of the tree at worst), but the append-only property is lost. Another problem is that higher level nodes may contain keys that have many 1's and thus become useless.
Signature files provide a space-time trade-off between full text scanning, which is slow but requires no overheads, and inversion, which is fast but requires expensive insertions and needs significant space overhead. Thus, signature-based methods have been applied in the following environments:
1. Medium-size databases. "Hyperties" (Lee et al. 1988), a hypertext package that is commercially available on IBM PCs, uses the SSF method, due to its simplicity, low space overhead, and satisfactory search time (3-10 seconds, for queries with low selectivities) on databases of
2. Databases with low query frequencies. In this case, it is not worth building and maintaining a B-tree inverted index; signature files provide a low-cost alternative, that avoids scanning the full text. This situation is probably true for message files in Office Automation; several prototype systems use the signature approach, like the Office Filing Project (Tsichritzis et al. 1983) at the University of Toronto, MINOS (Christodoulakis et al. 1986) at the University of Waterloo, the MULTOS project (Croft and Savino 1988) funded by the ESPRIT project of the European Community.
3. Due to the append-only insertion, signature-based methods can be used on WORM optical disks.
4. Due to the linear searching, signature files can easily benefit from parallelism. Stanfill and Kahle (1986) used signature files on the Connection Machine (Hillis 1985). Keeping the whole signature file in core, they can provide fast responses against databases that are
5. In distributed environments. In this case, keeping copies of signature files of all the sites can save remote-logins, for a modest space overhead.
6. Chang and Schek (1989) recommend signature files as a simple and flexible access method for records and "long fields" (=text and complex objects) in IBM's STAR-BUST extensible DBMS.
CHANG, W. W. and H. J. SCHEK. 1989. "A Signature Access Method for the Starbust Database System." Proc. VLDB Conference, pp. 145-53. Amsterdam, Netherlands, Aug. 22-25.
CHRISTODOULAKIS, S. 1987. "Analysis of Retrieval Performance for Records and Objects Using Optical Disk Technology," ACM TODS, 12(2), 137-69.
CHRISTODOULAKIS, S., and C. FALOUTSOS. 1984. "Design Considerations for a Message File Server." IEEE Trans. on Software Engineering, SE-10 (2), 201-10.
CHRISTODOULAKIS, S., F. Ho, and M. THEODORIDOU. 1986. "The Multimedia Object Presentation Manager in MINOS: A Symmetric Approach." Proc. ACM SIGMOD.
CHRISTODOULAKIS, S., M. THEODORIDOU, F. Ho, M. PAPA, and A. PATHRIA. 1986. "Multimedia Document Presentation, Information Extraction and Document Formation in MINOS: A Model and a System." ACM TOOIS, 4 (4).
CROFT, W. B, and P. SAVINO. 1988. "Implementing Ranking Strategies Using Text Signatures." ACM Trans. on Office Informations Systems (TOOIS), 6 (1), 42-62.
DEPPISCH, U. 1986. "S-tree: A Dynamic Balanced Signature Index for Office Retrieval." Proc. of ACM "Research and Development in Information Retrieval," pp. 77-87, Pisa, Italy, Sept. 8-10.
EWING, J., S. MEHRABANZAD, S. SHECK, D. OSTROFF, and B. SHNEIDERMAN. 1986. "An Experimental Comparison of a Mouse and Arrow-jump Keys for an Interactive Encyclopedia." Int. Journal of Man-Machine Studies, 24, (1) 29-45.
FALOUTSOS, C. 1985. "Access Methods for Text." ACM Computing Surveys, 17 (1), 49-74.
FALOUTSOS, C., and R. CHAN. 1988. "Fast Text Access Methods for Optical and Large Magnetic Disks: Designs and Performance Comparison." Proc. 14th International Conf. on VLDB, pp. 280-93, Long Beach, Calif. August.
FALOUTSOS, C., and S. CHRISTODOULAKIS. 1984. "Signature Files: An Access Method for Documents and its Analytical Performance Evaluation." ACM Trans. on Office Information Systems, 2 (4), 267-88.
FALOUTSOS, C., and S. CHRISTODOULAKIS. 1987. "Description and Performance Analysis of Signature File Methods." ACM TOOIS, 5 (3), 237-57.
FUJITANI, L. 1984. "Laser Optical Disk: The Coming Revolution in On-Line Storage." CACM, 27 (6), 546-54.
GALLAGER, R. G., and D. C. VAN VOORHIS. 1975. "Optimal Source Codes for Geometrically Distributed Integer Alphabets." IEEE Trans. on Information Theory, IT-21, 228-30.
GOLOMB, S. W. 1966. "Run Length Encodings." IEEE Trans. on Information Theory, IT-12, 399-401.
GONNET, G. H. 1982. "Unstructured Data Bases," Tech Report CS-82-09, University of Waterloo.
GONNET, G. H., and F. W. TOMPA. 1987. "Mind Your Grammar: A New Approach to Modelling Text." Proc. of the Thirteenth Int. Conf. on Very Large Data Bases, pp. 339-346, Brighton, England, September 1-4.
GUSTAFSON, R. A. 1971. "Elements of the Randomized Combinatorial File Structure." ACM SIGIR, Proc. of the Symposium on Information Storage and Retrieval, pp. 163-74, University of Maryland. April.
HASKIN, R. L. 1981. "Special-Purpose Processors for Text Retrieval." Database Engineering, 4 (1), 16-29.
HILLIS, D. 1985. The Connection Machine. Cambridge, Mass.: MIT Press.
HOLLAAR, L. A. 1979. "Text Retrieval Computers." IEEE Computer Magazine, 12 (3), 40-50.
HOLLAAR, L. A., K. F. SMITH, W. H. CHOW, P. A. EMRATH, and R. L. HASKIN. 1983. "Architecture and Operation of a Large, Full-Text Information-Retrieval System," in Advanced Database Machine Architecture, D. K. Hsiao, ed. pp. 256-99. Englewood Cliffs, N.J.: Prentice Hall.
KIMBRELL, R. E. 1988. "Searching for Text? Send an N-gram!" Byte, 13 (5) 297-312.
LEE, D. L., and C.-W. LENG. 1989. "Partitioned Signature File: Designs and Performance Evaluation." ACM Trans. on Information Systems (TOIS), 7 (2), 158-80.
LEE, R., C. FALOUTSOS, C. PLAISANT, and B. SHNEIDERMAN. 1988. "Incorporating String Search in a Hypertext System: User Interface and Physical Design Issues." Dept. of Computer Science, University of Maryland, College Park. Working paper.
LEWIS, E. P. 1989. "Animated Images for a Multimedia Database." Master's Thesis, Dept. of Computer Science, University of Maryland.
LIN, Z., and C. FALOUTSOS. 1988. "Frame Sliced Signature Files," CS-TR-2146 and UMI-ACS-TR-88-88, Dept. of Computer Science, University of Maryland.
LIPMAN, D. J., and W. R. PEARSON. 1985. "Rapid and Sensitive Protein Similarity Searches." Science, 227, 1435-41, American Association for the Advancement of Science, March 22.
MCILROY, M. D. 1982. "Development of a Spelling List." IEEE Trans. on Communications, COM-30, (1), 91-99.
MOOERS, C. 1949. "Application of Random Codes to the Gathering of Statistical Information." Bulletin 31, Zator Co., Cambridge, Mass. Based on M.S. thesis, MIT, January 1948.
NOFEL, P. J. 1986. "40 Million Hits on Optical Disk." Modern Office Technology, 84-88. March.
PETERSON, J. L. 1980. "Computer Programs for Detecting and Correcting Spelling Errors." CACM, 23 (12), 676-87.
PRICE, J. 1984. "The Optical Disk Pilot Project At the Library of Congress." Videodisc and Optical Disk, 4 (6), 424-32.
ROBERTS, C. S. 1979. "Partial-Match Retrieval via the Method of Superimposed Codes." Proc. IEEE, 67 (12), 1624-42.
SACKS-DAVIS, R., A. KENT, and K. RAMAMOHANARAO. 1987. "Multikey Access Methods Based on Superimposed Coding Techniques" ACM Trans. on Database Systems (TODS), 12 (4), 655-96.
SACKS-DAVIS, R., and K. RAMAMOHANARAO. 1983. "A Two Level Superimposed Coding Scheme for Partial Match Retrieval." Information Systems, 8 (4), 273-80.
SALTON, G., and M. J. MCGILL. 1983. Introduction to Modern Information Retrieval. New York: McGraw-Hill.
STANDISH, T. A. 1984. "An Essay on Software Reuse." IEEE Trans. on Software Engineering, SE-10 (5), 494-97.
STANFILL, C., and B. KAHLE. 1986. "Parallel Free-Text Search on the Connection Machine System." CACM, 29 (12), 1229-39.
STIASSNY, S., 1960. "Mathematical Analysis of Various Superimposed Coding Methods." American Documentation, 11 (2), 155-69.
THOMA, G. R., S. SUTHASINEKUL, F. A. WALKER, J. COOKSON, and M. RASHIDIAN. 1985. "A Prototype System for the Electronic Storage and Retrieval of Document Images." ACM TOOIS, 3 (3).
TSICHRITZIS, D., and S. CHRISTODOULAKIS. 1983. "Message Files." ACM Trans. on Office Information Systems, 1 (1), 88-98.
TSICHRITZIS, D., S. CHRISTODOULAKIS, P. ECONOMOPOULOS, C. FALOUTSOS, A. LEE, D. LEE, J. VANDENBROEK, and C. WOO. 1983. "A Multimedia Office Filing System." Proc. 9th International Conference on VLDB, Florence, Italy, October-November.
4.1 INTRODUCTION
Electronic office filing (Tsichritzis and Christodoulakis 1983; Christodoulakis et al. 1986). Computerized libraries. For example, the U.S. Library of Congress has been pursuing the "Optical Disk Pilot Program" (Price 1984; Nofel 1986), where the goal is to digitize the documents and store them on an optical disk. A similar project is carried out at the National Library of Medicine (Thoma et al. 1985). Automated law (Hollaar 1979) and patent offices (Hollaar et al. 1983). The U.S. Patent and Trademark Office has been examining electronic storage and retrieval of the recent patents on a system of 200 optical disks. Electronic storage and retrieval of articles from newspapers and magazines. Consumers' databases, which contain descriptions of products in natural language. Electronic encyclopedias (Ewing et al. 1986; Gonnet and Tompa 1987). Indexing of software components to enhance reusabililty (Standish 1984). Searching databases with descriptions of DNA molecules (Lipman and Pearson 1985). Searching image databases, where the images are manually annotated (Christodoulakis et al. 1986). A similar approach could be used to search a database with animations, if scripted animation is used (Lewis 1989). Text databases are traditionally large. Text databases have archival nature: there are insertions in them, but almost never deletions and updates.
10-15% [Christodoulakis and Faloutsos 1984], as opposed to 50-300% that inversion requires [Haskin 1981]); moreover, they can handle insertions more easily than inversion, because they need "append-only" operations--no reorganization or rewriting of any portion of the signatures. Methods requiring "append-only" insertions have the following advantages: (a) increased concurrency during insertions (the readers may continue consulting the old portion of index structure, while an insertion takes place) (b) these methods work well on Write-Once-Read-Many (WORM) optical disks, which constitute an excellent archival medium (Fujitani 1984; Christodoulakis 1987).4.2 BASIC CONCEPTS
Word Signature
-----------------------------------
free 001 000 110 010
text 000 010 101 001
-----------------------------------
block signature 001 010 111 011
Figure 4.1: Illustration of the superimposed coding method. It is assumed that each logical block consists of D=2 words only. The signature size F is 12 bits, m=4 bits per word.
Fd = Prob{signature qualifies/block does not}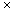
N binary matrix. Previous analysis showed that, for a given value of F, the value of m that minimizes the false drop probability is such that each row of the matrix contains "1" 's with probability 50 percent. Under such an optimal design, we have (Stiassny 1960):Fd = 2-m
F1n2 = mD
Table 4.1:. Symbols and definitions
Symbol Definition
--------------------------------------------------------
F signature size in bits
m number of bits per word
D number of distinct noncommon words per document
Fd false drop probability
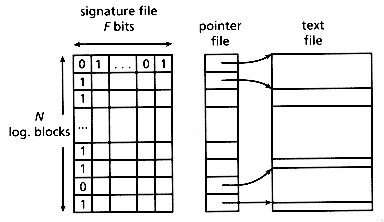
Figure 4.2: File structure for SSF
the storage overhead, the response time on single word queries, the performance on insertion, as well as whether the insertion maintains the "append-only" property. Sequential storage of the signature matrix
without compression
sequential signature files (SSF)
with compression
bit-block compression (BC)
variable bit-block compression (VBC)
Vertical partitioning
without compression
bit-sliced signature files (BSSF, B'SSF))
frame sliced (FSSF)
generalized frame-sliced (GFSSF)
with compression
compressed bit slices (CBS)
doubly compressed bit slices (DCBS)
no-false-drop method (NFD)
Horizontal partitioning
data independent partitioning
Gustafson's method
partitioned signature files
data dependent partitioning
2-level signature files
S-trees
Figure 4.3: Classification of the signature-based methods
4.3 COMPRESSION
data 0000 0000 0000 0010 0000
base 0000 0001 0000 0000 0000
management 0000 1000 0000 0000 0000
system 0000 0000 0000 0000 1000
----------------------------------------
block
signature 0000 1001 0000 0010 1000
Figure 4.4: Illustration of the compression-based methods. With B = 20 and n = 1 bit per word, the resulting bit vector is sparse and can be compressed.
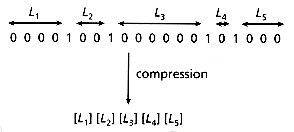
Figure 4.5: Compression using run-length encoding. The notation [x] stands for the encoded value of number x
4.3.1 Bit-block Compression (BC)
b
<-->
sparse vector 0000 1001 0000 0010 1000
-------------------------------------------
Part I 0 1 0 1 1
Part II 10 0 0
Part III 0011 10 00
Figure 4.6: Illustration of the BC method with bit-block size b = 4.
0 1 0 1 1 | 10 0 0 | 00 11 10 00
Figure 4.7: BC method--Storing the signature by concatenating the parts. Vertical lines indicate the part boundaries.
4.3.2 Variable Bit-block Compression (VBC)
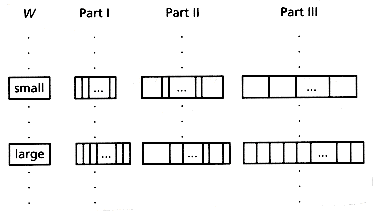
Figure 4.8: An example layout of the message signatures in the VBC method.
4.3.3 Performance
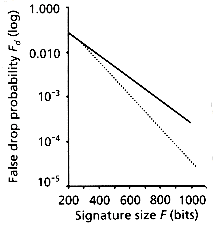
Figure 4.9: Comparison of Fd of BC (dotted line) against SSF (solid line), as a function of the space overhead Ov. Analytical results, from Faloutsos and Christodoulakis (1987).
50 percent savings in false drops for documents with D = 40 vocabulary words each.4.4 VERTICAL PARTITIONING
4.4.1 Bit-Sliced Signature Files (BSSF)
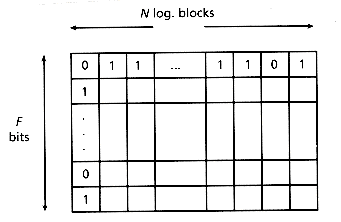
Figure 4.10: Transposed bit matrix
Winchester, 1350 Series Seek time (avg) = 28 ms; Latency time (avg) = 8.33 ms; Transfer rate = 10 Mbits/sec; Sector size = 512 bytes.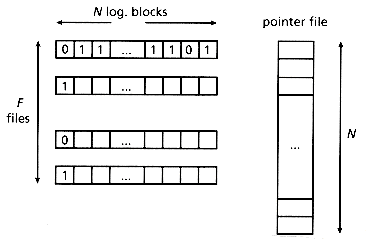
Figure 4.11: File structure for Bit-Sliced Signature Files. The text file is omitted.
4.4.2 B'SSF, a Faster Version of BSSF
4.4.3 Frame-Sliced Signature File
Word Signature
free 000000 110010
text 010110 000000
doc. signature 010110 110010
Figure 4.12: D = 2 words. F = 12, s = 6, k = 2, m = 3. The word free is hashed into the second frame and sets 3 bits there. The word text is hashed into the first frame and also sets 3 bits there.
4.4.4 The Generalized Frame-Sliced Signature File (GFSSF)
When k = F, n = m, it reduces to the BSSF or B'SSF method. When n = 1, it reduces to the FSSF method. When k = 1, n = 1, it becomes the SSF method (the document signature is broken down to one frame only).4.4.5 Performance
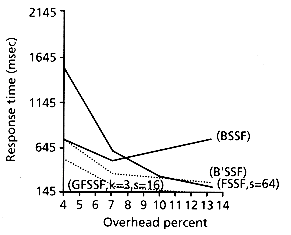
Figure 4.13: Response time vs. space overhead: a comparison between BSSF, B'SSF, FSSF and GFSSF. Analytical results on a 2.8Mb database.
1 Kb. Each document contained D = 58 distinct noncommon words.4.5 VERTICAL PARTITIONING AND COMPRESSION
4.5.1 Compressed Bit Slices (CBS)
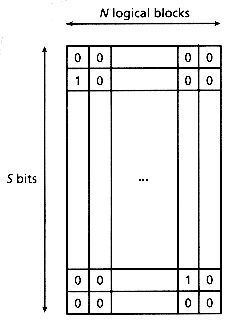
Figure 4.14: Sparse bit matrix
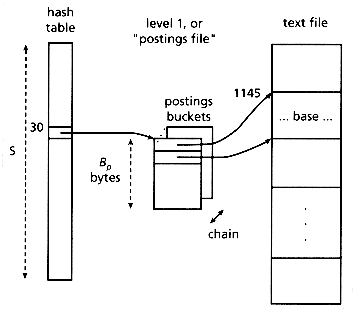
Figure 4.15: Illustration of CBS
4.5.2 Doubly Compressed Bit Slices (DCBS)
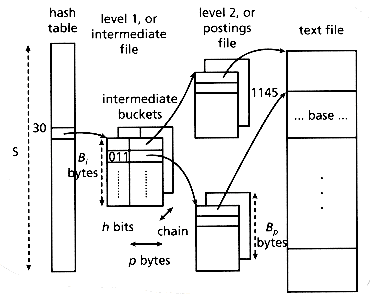
Figure 4.16: Illustration of DCBS
4.5.3 No False Drops Method (NFD)
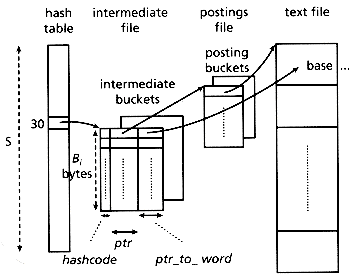
Figure 4.17: Illustration of NFD
8 characters long (Peterson 1980), and (2) the records of the intermediate file have fixed length. Thus, there is no need for a word delimiter and there is no danger for a word to cross bucket boundaries.4.5.4 Performance
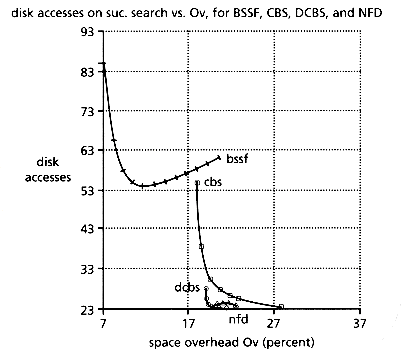
Figure 4.18: Total disk accesses on successful search versus space overhead. Analytical results for the 2.8 Mb database, with p = 3 bytes per pointer. Squares correspond to the CBS method, circles to DCBS, and triangles to NFD.
4.6 HORIZONTAL PARTITIONING
4.6.1 Data Independent Case
Gustafson's method
C(p1, 1) + C(p2, 2) + . . . + C(p6, 6)
Partitioned signature files
4.6.2 Data Dependent Case
Two-level signature files
106 records (with 128 bytes per record on the average) reported response times as low as 0.3 seconds for single word queries, when 1 record matched the query. The BSSF method required 1-5 seconds for the same situation.S-tree
4.7 DISCUSSION
200 Kb (after compression). Thanks to the low overhead, the whole package (software, data, and indices) fits in floppy diskettes. Another commercial product (Kimbrell 1988) is also reported to use signature files for text retrieval.10 times larger than the available main memory storage.REFERENCES