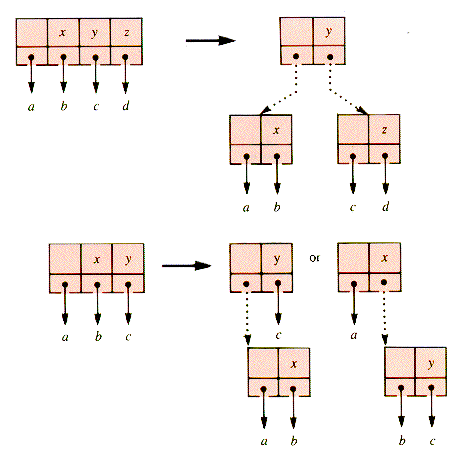
A 3-ode or a 4-ode can be modeled with a binary subtree, bound together with links that are called red links to distinguish them from the links of the 2-3-4 tree in which they occur, called black links. With the use of dashed lines to represent red links, the tree is shown in Figure U.1 . In a tree represented this way, 4-nodes are characterized by having a subtree root with red links to both children.
The depth of an RBT (Red-Black Tree) binary tree may be twice that of the corresponding 2-3-4 tree, but it is still proportional to the log of the number of keys in it. The links of an RBT need to be flagged with their color; and, if the nodes are entirely supported in arrays, the sign bit of the pointer index may be used. An alternate scheme, used here, is to flag a node with the color of the link that leads to it from its parent. It is convenient to include a field in the node that contains a pointer Up to the parent of the node.
The creation operation becomes:
procedure Create(rbt,LeftChild,RightChild)
NEW(rbt)
rbt.Up
rbt
rbt
rbt
rbt
end {Create
The search operation, likely to be used more than any other, is then:
procedure RBSearch(rbt,SearchKey,Node,Found)
Node
Parent
while Nodeu do {u is the universal tail.
if SearchKey = Node
then Found
return
endif
Parent
if SearchKey < Node
then Node
else Node
endif
endwhile
Found
Node
end {RBSearchInsertion includes a similar traverse that splits 4-nodes as they are encountered. The splitting operation is applied to the root node, or to a 4-node reached from a 2-node (a 2-4 subtree) or a 4-node reached from a 3-node (a 3-4 subtree).
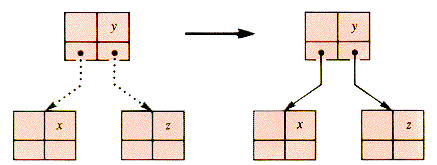
The root-node split is shown schematically in Figure U.2 . The split simply changes two red links to black links. No key value is actually shifted.
The 2-4 subtree split schematically changes the (2-node to 4-node subtree) to a (3-node to two 2-nodes) subtree, shown in Figure U.3.
Once again, no information is altered except the color of the links.
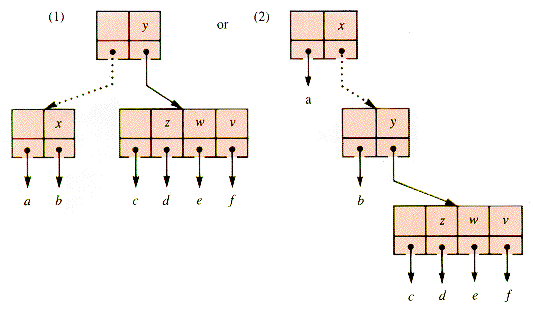
In the case of a 3-4 subtree, the 3-node may have either binary node as the subtree root. For example, Figure U.4 may be represented in either of the ways shown in Figure U.5 .
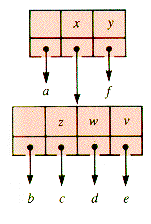
Similarly, the 3-4 subtree of Figure U.6 has two representations, shown in Figure U.7, both having a red grandparent-parent link relative to the 4-node.
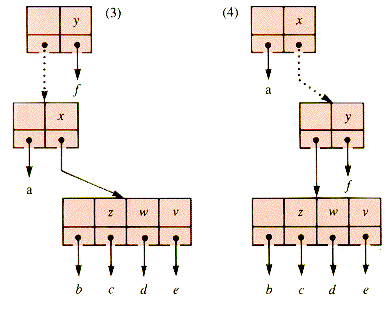
When the grandparent-parent link of a 4-node is red, a simple color-shift applied during splitting of the node produces two red links in sequence, as Figure U.8 illustrates for case (2) (from Figure U.5).
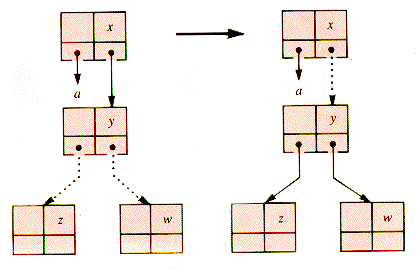
This is prevented for the case of Figure U.4 by a rotation, in which the lexicographic order of the keys is unchanged, but the relative levels of two nodes are switched. A rotation switches the binary-tree levels of the two keys in a 3-node and shifts links to their parent and children to match. A rotation of keys x and y is considered to be the rotation of the child and grandchild of the node n, as depicted in Figure U.9. After this rotation, splitting the right child of gc does not produce two red links in succession.
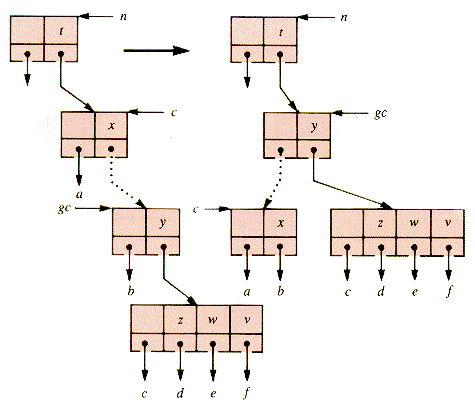
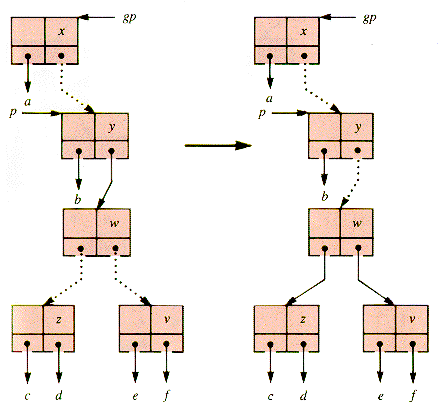
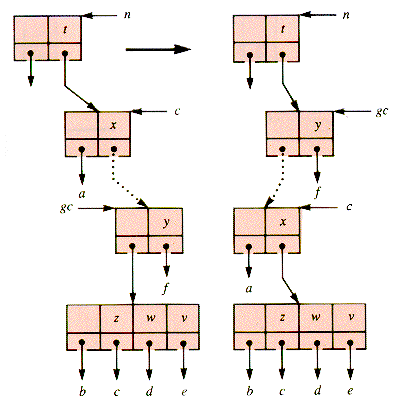
If a 4-node is the middle child of a 3-node, it remains a middle child after rotation and retains a red grandparent-parent link, as shown in Figure U.10. One approach to resolving this problem is a prior rotation involving the root of the 4-node itself, shown in Figure U.11. Figure U.12 shows the result when this rotation is followed by a rotation at the (original) great-grandparent of node.
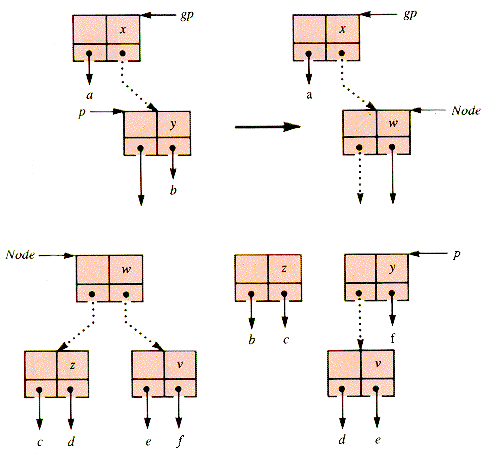
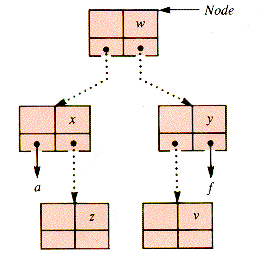
With color changes at z and f, this double rotation has the effect in the RBT shown in Figure U.13. None of these rotations change the number of levels in the 2-3-4 tree.
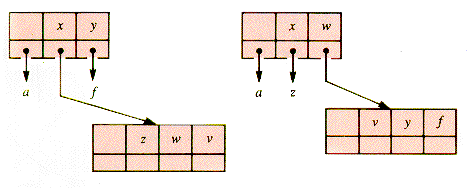
It is convenient to design a generic rotation that internally traces the path from node to grandchild in order to detect left and right branches:
procedure Rotate(SKey,n)
if SKey > n
then c
else c
endif
if SKey > c
then gc
ggc
c
gc
else gc
ggc
c
gc
endif
if SKey > n
then n
else n
endif
gc
c
ggc
Color
gc
c
end {RotateThe middle-child case is characterized by the alteration in direction of grandparent-parent and parent-node links and requires a rotation to change it into the other case. The splitting operation thus becomes:
procedure RBSplit(SKey,Node)
p
if p
then gp
ggp
if SKey < gp
then Rotate(SKey,gp)
if SKey < p
then p
Node
else p
Node
endif
endif
Rotate(SKey,ggp)
endif
if Node
Node
Node
end {RBSplitThe insertion procedure repeats the search process explicitly, except that it also splits 4-nodes during the traverse. The use of a universal tail node u allows the new node to be treated as the root of a 4-node subtree and immediately split upon entry to properly adjust its relationship to its parent:
procedure RedBlackIn(rbt,NewKey,NewValue)
if rbt = u
then Create(rbt,u,u)
rbt
rbt
return
endif
Node
while Node
if NewKey = Node
then return {or otherwise deal with
endif {a duplicate key.
Parent
if Node
then RBSplit(NewKey,Node)
else if NewKey < Node
then Node
else Node
endif
endif
endwhile
Create(Node,u,u)
with Node do
Up
Value
Key
Red
endwith
if NewKey < Parent
then Parent
else Parent
endif
RBSplit(NewKey,Node)
end {RedBlackIn
Problem not immediate, but requiring no major extensions of text
PU.1 Draw the sequence of Red-Black trees that would be created by entering the months in calendar order if they are to be kept in alphabetical order.
Program for trying it yourself
PGU.1 Write a program that will accept strings and place them in a Red-Black tree ordered lexicographically. The program should display the tree after entries. Test it with the months of the year, entered in reverse calendar order.
Program