


In section B, the collision of keys mapped to the the same range index in a hash table was resolved by hunting through the table for an empty cell during the STORE operation and for the key during a RETRIEVE operation. The hash table was a static structure, and the actual location of a hashed key in the table was not always the direct result of the hashing function.
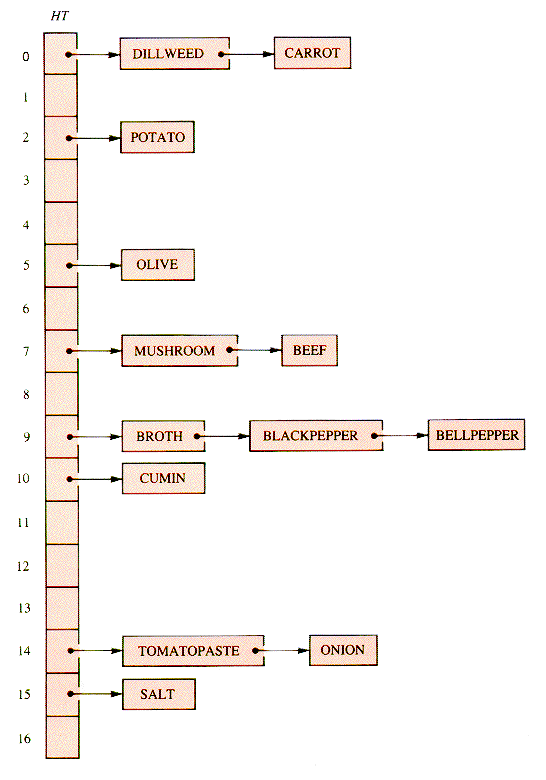
An alternate method is to use a table cell as the header of a linked list that contains all of the keys that hash to the index of that cell. Reaching the head of the list is an immediate result of hashing the key, although the list must be searched for retrieval. (The STORE operation may probe the list to detect duplicate entries.)
With the definitions of section B and the use of q, m = 17, Hash = h, and alphabetical entry order, a list-header hash table for the list of ingredients of section 2.5 is shown in Figure L.1.

The major change introduced by chaining lies in the search for a key in the linear list of a header. The function Probe used by both StoreHT and RetrieveHT is a list-walk:
function Probe(Start,s) {O(m)
pH[Start]
while pNIL do
if p.Key = s then exit endif
pp
.Link
endwhile
return p
end {Probe
procedure StoreHT(Key) {O(Probe)
kHash(Key)
pProbe(k,Key)
if p = NIL
then NEW(q)
q.Value
Key
q.Link
HT[k]
.Link
HT[k].Link
q
else {deal with a duplicate entry
endif
end {StoreHT
function RetrieveHT(Key) {O(Probe)
kHash(Key)
pProbe(k,Key)
if p = NIL
then {report not there
else return p
endif
end {RetrieveHTThis logic retrieves the location or presence of a key in the table, enough for many applications. In other applications it must be expanded somewhat to allow deletion of keys from the table--something difficult to manage with a static hash table. A chained table can be an excellent choice for a hash table from which deletion is to occur.
The chained hash table has a slight advantage over the static table in the easy detection or inclusion of duplicate entries. If the keys are 20-character (20-byte) strings and if pointers require 2 bytes, the static table occupies m X 20 bytes. For n entries, the chained table requires 2 X m + n X (20 + 1) bytes. As n/m  0, this approaches 2 X m. For keys that are themselves pointers, chaining uses more space. A deeper analysis is beyond the scope of this book, but double-hashing of unchained tables is a common professional choice.
0, this approaches 2 X m. For keys that are themselves pointers, chaining uses more space. A deeper analysis is beyond the scope of this book, but double-hashing of unchained tables is a common professional choice.
Problem not immediate, but requiring no major extensions of the text
PL.1 Design the procedures and functions that would allow deletion from a chained hash table.
Program for trying it yourself
PGL.1 Write a program that accepts identifiers of up to 12 characters in length, converts them to an integer with q, and stores them in a chained hash table HT with the use of Hash = h and m = 47. The program should report the number of collisions, the average number of links followed by Probe, and the loading factor.
Program