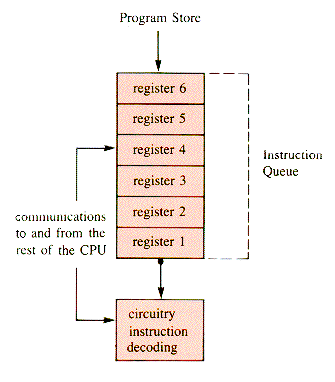



Some microprocessors, such as the Intel 8086, have an instruction queue built into the CPU [INTEL, 1979]. The motivation is that the CPU execution cycle contains essentially four phases: execution, fetch, read, and write. Here read, write, and fetch refer to sending and receiving information from the CPU itself. In particular, write refers to the sending of information to some address that may be associated with a display, but may just be an update of a memory location. The effect of the write depends on the instruction that commands it, and the address. The read phase involves acquiring data from some address, which may be in memory or may be associated with a terminal. Instructions may or may not read and write in this general sense when they are executed, depending upon their function. The term fetch specifically refers to acquiring an instruction from memory. The crucial fact is that the CPU is otherwise idle during the fetch operation, unless it is possible to overlap the phases. With overlap, some of the phases can be done simultaneously by the hardware. The instruction queue that makes this possible is a set of 6 registers, which are storage locations, like memory cells, except that they are in the CPU itself, not in memory. (Register is the more general term; memory cells are registers used in a particular way.) The scheme is a queue, as illustrated in Figure J.1.
The IQ (Instruction Queue) is used to store the next few instructions that are expected to be executed in order. Execution of a branch operation (conditional or not) will cause the next instruction to be taken out of sequence, and so the next instruction may need to be fetched immediately and the instruction queue reloaded from the new point. Without concern for branches, however, fetches into the IQ may take place during execution of the current instruction.
A schematic trace of the overlap can be given using exec, wr, f, and rd as abbreviations for execute, write, fetch, and read, respectively. A simplified example of instructions 1,2,3,4, and 5 during eight units of time might look like Figure J.2.

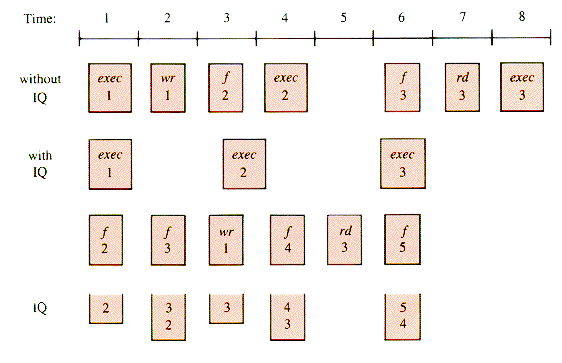
The amount of time saved by the IQ mechanism depends upon a variety of factors:
The speed at which instructions can be moved from the IQ to the decoder, relative to the time required for a fetch from memory. It might be faster by a factor of 1000; and, if so, the IQ-to-decoder move is negligible.
The amount of time spent in the fetch phase, compared to time spent during execute, read, and write phases. A rough estimate is that fetches can use 10 - 40 percent of the CPU time if there is no overlap.
The frequency of branch operations. A rough estimate is that 1 instruction in 16 is a branch.
The actual time saved in execution depends so heavily on the particulars of the instruction stream that it needs to be determined or at least verified experimentally. A speedup of 15 percent or so due to the IQ would be a modest expectation.
Program PGJ.1 is appropriate at this point.
The use of an instruction queue is a simple form of a more extensive overlap of instruction execution called pipelining. Execution of an instruction in a processor is actually the execution of a sequence of more primitive operations, called microcode. Microcode is designed to be neatly done with electronic circuitry. The instruction decoder, in effect, invokes a procedure in which the statements are microcode operations. Such procedures may include subprocedures and calls on standard (microcode) utility subprocedures, and so on, just like any computer coding. (Some people program in microcode for a living. It may be a relief to know that the buck stops there--the substrate that supports microcode is engineering, not programming.) The meaning of an instruction is determined by a microcode program. Some machines are even designed to allow users to redesign the instruction set by re(micro)programming them.
The circuits controlled by microcode instructions do not have to be idle while other circuits are at work. Pipelining allows parts of several instructions to be moving through the execution system at the same time. The ultimate set of divisions of an instruction that permits pipelining is not (execute, read, write, and fetch), but the set of available microcode operations.
The fetch of instructions from the program store is an execution bottleneck, and so is the fetch of data, which can be relieved with the use of a cache memory. (Data, from the viewpoint of the CPU, include instructions--whatever comes from memory.) A cache memory is memory that can be accessed much more rapidly than the main store because of the way it is constructed. It costs more, else it would simply replace the main store, and so it is relatively small.
Effective use of a buffer, such as a cache memory, is made when it is full of precisely those values that will be needed next. This can be done with high success in several ways, some involving queueing.
Typically, a cache memory ranges from 1K (1024 bytes) to 64K and is 5 to 10 times as fast as main memory, having perhaps 100 nsec (nanoseconds, 10-9 seconds) for an access time. Circuitry is designed into the machine to keep track of what is in the cache; it is a "cache directory," such as Figure J.3 shows.
When a memory-reference is made, if the information is in the cache, the cache is used for the read or store. An 85-95 percent "hit rate" is typical, but it depends on some strategy for keeping those data most likely to be used soon in the cache. The hit rate depends upon how local the memory references tend to be.
One way to enhance the hit rate involves dividing the cache into areas that will be called segments here. Data are fetched from the main store in chunks of segment size, and the collection of segments is treated as a queue (or perhaps a priority queue). A directory of segments that are currently in the cache is maintained. Whenever a segment is accessed, whether or not it is already in the cache, it can be moved to the tail of the queue. The head of the queue is then a segment that has been idle longer than any other segment and may be bumped by addition of a new segment.
A generalization of a cache queue is a cache priority queue, which allows the use of a variety of strategies for determining which segments to retain in the cache and which to swap for a currently needed value.
Programs for trying it yourself
PGJ.1 Write a program that explores the effect of an IQ. Instructions are to be chosen at random, with:
100 percent requiring an execute phase and a fetch phase, of 6 and 10 units of time, respectively
25 percent requiring an additional read phase of 8 units of time
50 percent requiring an additional write phase of 8 units of time
20 percent are branch operations that empty an IQ if it is being used
Determine the time required for each of five runs of 40 instructions each, both with and without an IQ of six registers. Run again with the times for execute and fetch switched to 10 and 6, respectively.
PGJ.2 Write a program that explores the effect of a cache memory. A sequence of memory references are chosen to randomly call on segments in the cache memory 85 percent of the time. Two units of time are required for retrieval from the cache and 10 for direct retrieval from memory (which brings a new segment to the cache). The tail segment is twice as likely as the next to be hit; it in turn is twice as likely as the next, and so on. The overhead cost of moving a segment to the tail is one unit of time. There are six segments in the cache. Choose five sequences of 40 memory requests each, and determine the total retrieval time needed for them.
PGJ.3 Combine PGJ.1 and PGJ.2 to determine the effect of an IQ and a cache acting in concert.
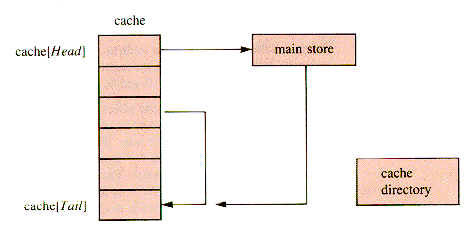
Figure J.3
Programs