SECTION D: INTEGER ARITHMETIC OF UNBOUNDED PRECISION

The phrase "unbounded precision" means that the program providing the calculation itself places no limitation on the number of digits in a value. There are limitations to the storage capacity of any computing system; but they are generally very large relative to values that are likely to be used, and the program simply ignores that bound.

The program Unbound presented in this section is a simulation of a calculator used in infix mode: a value, an operator, and then a value are entered and the result display is prompted by the entry of a character " = '' or one that represents another operator. The functions provided are addition ("+"), subtraction ("-"), multiplication ("*"), division ("/"), display ("="), clear the accumulator ("C''), and quit ("Q"). The inclusion of M + (add to memory), M - (subtract from memory), MRC (recover from memory), and MCL (memory clear) are left as a challenge.

The program Unbound is developed in this section, rather than simply described or listed, in order to document the series of design decisions implemented by the program. The logic of Unbound is clarified by developing it in pseudocode and then translating that logic into Pascal.

D.1 The Entry Sequence

A crucial feature of a calculator is that it is fairly robust: mistaken entries do little harm, and that feature should be retained in a simulating program. The possibilities for ambiguous entries are much increased with the use of a terminal keyboard in place of the more restricted calculator keypad. In that spirit, extraneous characters are ignored. The accepted characters are digits 0 -9 and operators ''+'', "-", ''*'', ''/'', '' = '', ''C'', ''Q''. All others are ignored. For example, A17B3 is accepted as 173. For the sake of robustness, division by 0 simply results in 0.

The basic response of the program is designed to deal with entry sequences such as: 24 + 9 =, which results in a display of 33 and the retention of that value in an accumulator (represented by the variable AC). A string of digits that designates a number is terminated by an operator, and so it is (value,operator)-pairs that are accepted by the program. Although an operator terminates the entry of a number, it is the previous operator that usually determines the action. (Operators such as ''C" and ''Q'' are exceptions.) In more detail, if the entering value is X and the result of arithmetic is held in AC, the action of this sequence can be traced as shown in Table D.1.

Table D.1

Entries   X  NewOp  Op  AC

--------------------------

                     C   0

  24+    24    +     C  24

  9=      9    =     +  33

The operation of most calculators is more complex than this example seems to imply. What, for example, is the result of the following entry sequences?

- 24 + 9 =

- 24 + 9 +

24 + +

24 + + =

24 + + + =

The results generated by the program developed here are -15, -15, 24, 48, and 72, respectively. The last of these is not standard, but it is convenient to have each new operator invoke the response of the previous one. If no new X is entered, the AC value is used as X.

D.2 Utility Routines

A procedure Preface is used to initialize variables and provide instructions to the user; Clear is used to set registers such as AC to zero; and Display writes out the value in the accumulator AC. These utility routines are supplemented by arithmetic procedures that act on AC.

The procedure ValueIn that extracts the tokens X and NextOp also returns a Boolean flag NoX to indicate the presence of a numeric value between operators. The command-shell executes the previous operator, Op, in response to the next operator, NextOp. If no X-value is entered withNextOp, then the current value of AC is copied into X. Operators "Q'' and ''C'' require immediate response. When "Q'' is NextOp, it causes immediate termination of the program. When NextOp is ''C'' both AC and X are cleared, and Op is set to "C'' also. When Op is either "C'' or ''='', and an X-value is entered with NextOp, the X-value becomes the new AC value.

The command-shell program that results is:

program UnBound

Preface

Done  FALSE

Op  'C'

repeat

ValueIn(X,NoX,NextOp)

if NextOp = 'Q'

then Done  TRUE

else if NextOp = 'C'

then Clear(AC)

Clear(X)

Op  'C'

endif

if NoX then X  AC endif

case of Op

'=', 'C': Swap                     {AC with X

'+'     :Add(AC,X)

{'-', '*', '/' are similar to '+'}

endcase

endif

Op  NextOp

Display

until Done

end {UnBound

The next level of detail is dependent on the implementation of values, and that implementation must allow assignments X AC and AC X for unbounded strings of digits. Values need to carry a sign, have leading zeroes suppressed for the sake of efficiency and display, be compared in magnitude (left-to-right for corresponding digits), and be used right-to-left in arithmetic operations. The chosen implementation for AC and X is a pointer to a header of a doubly linked list. Such a list plays the role of a register--a storage location directly associated with computation. For reasons that only become apparent when operations are examined in detail, it is convenient to carry one leading zero and link it to itself. When AC 743, the resulting register structure is shown in Figure D.1.

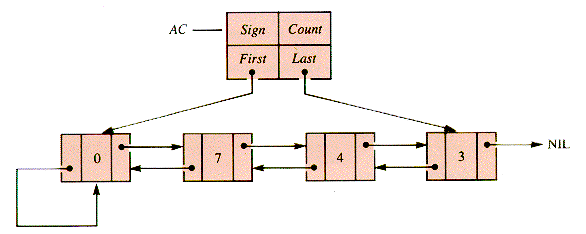
Figure D.1

The Sign field is Boolean, with TRUE corresponding to positive values--making tests involving signs more convenient.

A header such as AC or X can then be initialized by:

procedure NewRegister(R)

NEW(d)

d  .Left  d

d  .Value  0

d  .Right  NIL

NEW(R)

R  .First  d

R  .Last  d

R  .Sign  TRUE

R  .Count  0

end  {NewRegister

Setting an initialized register back to zero can be even simpler:

procedure Clear(R)

R  .Last  R  .First

R  .Count  0

R  .Sign  TRUE

end  {Clear

This procedure, however, does not recover the (possibly many) digit nodes that were in the register R. A more practical version of Clear is:

procedure Clear(R)

p  R  .Last

q  p  .Left

while  p  R  .First do

DISPOSE(p)

p  q

q  p  .Left

endwhile

p  .Right  NIL

R  .Last  p

R  .Count  0

R  .Sign  TRUE

end  {Clear

The speed of arithmetic operations is directly dependent on the number of digits involved, and so removal of duplicate leading zeroes is an essential part of housekeeping:

procedure Compact(R)

p  R  .First

q  p  .Right

while q  NIL do

if q  .Value  0

then exit

else t  q  .Right

DISPOSE(q)

R  .Count  R  .Count - 1

P  .Right  t

q  t

if t  NIL

then t  .Left  p endif

endif

endwhile

if R .Count = 0 then R .Last  R .First endif

end {Compact

Note: The pair of tests at the top of this loop require a fair amount of modification when implemented in Pascal because the condition:

(q  NIL) AND (q  .Value  0)

is risky. A more direct translation results from the use of GOTO to implement exit.

On the principle of "never trust the user," compaction is included as the last action in ValueIn.

The input-token generator ValueIn is:

procedure ValueIn(X,NoX,NextOp)

NoX  TRUE

Clear(X)

Read(ch)

while NOT (ch IN OperatorSet) do

if ch IN [0..9]

then NoX  FALSE

NEW(d)

d  .Right  NIL

d  .Value  ORD(ch) - ORD('0')

d  .Left  X  .Last

X  .Last  .Right  d

X  .Last  d

X  .Count  X  .Count + 1

endif

Read(ch)

endwhile

NextOp  ch

Compact(X)

end {ValueIn

D.3 Arithmetic Operations

The fundamental operation of arithmetic is addition, but it becomes subtraction when the signs of the operands differ. When done by hand, the value of smaller magnitude is subtracted from the other. One simple approach to addition is based on two steps:

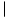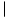
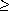
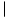1. Compare AC and X and switch them if necessary to insure that AC X.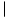

2. If the signs agree, then add magnitudes with procedure Carry; otherwise, subtract the magnitudes with procedure Borrow.

The resulting logic is:

procedure Add(X)

R  LargerOf(AC,X)

if R = X

then X  AC

AC  R

endif

if X  .Count = 0 then return endif

if AC  .Sign = X  .Sign

then Carry(AC,X)

else Borrow(AC,X)

endif

end  {Add

function LargerOf(AC,X)        {O(n) Assumes compacted operands

if AC  .Count > X  .Count  then return AC endif

if X  .Count > AC  .Count  then return X endif

k  AC  .Count

pAC  AC  .First  .Right

pX  X  .First  .Right

while k > 0 do

if pAC  .Value > pX  .Value  then return AC endif

if pAC  .Value < pX  .Value  then return X endif

pAC  pAC  .Right

pX  pX  .Right

k  k - 1

endwhile

return AC                    {X = AC

end  {LargerOf

Note: The returns are replaced by a nest of IF-statements in Pascal. Add, Subtract, Multiply, and Divide all may switch X and AC to avoid copying a long list of digits, and so X is a VAR parameter in the Pascal implementation.

The last carry operation can create a new digit (as in 997 + 18), which is signaled by a carry after the last X-digit has been added to AC. The last borrow can propagate to the left (as in 10003 - 4), but that can be handled by continuing to subtract the leading zero node, X 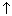.First. With these problems recognized:

procedure Carry(X)

pAC  AC .Last

pX  X  .Last

Over  0

for k = 1 to AC  .Count do

Sum  pAC  .Value + pX  .Value + Over

if Sum > 9

then Over  1

pAC  .Value  Sum - 10

else Over  0

pAC  .Value  Sum

endif

pAC  pAC  .Left

pX  pX  .Left

next k

if Over > 0

then NEW(d)

d  .Right  pAC  .Right

d  .Left  pAC

pAC  .Right  .Left  d

pAC  .Right  d

d  .Value  Over

AC  .Count  AC  .Count + 1

endif

end {Carry

procedure Borrow

pAC  AC  .Last

pX  X  .Last

Loan  0

for k = 1 to AC  .Count do

Difference  pAC .Value - pX  .Value - Loan

if Difference < 0

then Loan  1

pAC  .Value  Difference + 10

else Loan  0

pAC  .Value  Difference

endif

pAC  pAC  .Left

pX  pX  .Left

next k

Compact(AC)

end {Borrow

With Add complete, subtraction becomes very simple:

procedure Subtract(X)

X  .Sign  NOT X  .Sign

Add(X)

end {Subtract

Multiplication can be done by repeated addition in two ways: 47 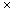31 = (47 + 47 + . . . + 47, 31 times) and 47 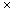31 = (47 + 3 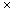470). The latter approach is used here. It will square 2 raised to the 96th power in a few seconds on an inexpensive microcomputer (after compilation by a $30 Pascal compiler). This operation would take years by repeated addition.

Several values are involved in multiplication: the original operands X and AC, the shifting values Y (such as 47, 470, . . . ), the product of a digit of X with a Y, say M, and the running sum of these products. AC supplies the original Y and then may contain the running sum. The product sign must be determined but not affect the use of Add to multiply magnitudes, and a value with a minimal number of digits should be used to control the multiplication loop. This housekeeping is done by:

procedure SetUp

Y  AC

NewRegister(AC)

New Register(M)

R  LargerOf(Y,X)

if R = X

then X  Y

Y  R

endif

NewSign  (Y  .Sign = X  .Sign)

X  .Sign  TRUE

Y  .Sign  TRUE

Clear(AC)

end {SetUp

A routine is needed to shift successive products one digit to the left. One approach is to shift Y:

procedure ShiftLeft(Y)

NEW(d)

d  .Value  O

d  .Right  NIL

d  .Left  Y .Last

Y  .Count  Y  .Count + 1

Y  .Last  .Right  d

Y  .Last  d

end {ShiftLeft

Multiplication then can be done with:

procedure Multiply(X)

SetUp

if X  .Count = 0 then return endif

pX  X  .Last

for j = 1 to X  .Count do

Over  0

MakeCopy(M,Y)

pM  M  .Last

pX  X  .Last

v  pX  .Value

for k = 1 to M  .Count do

Product  pM  .Value * v + Over

pM  .Value  Product MOD 10

Over  Product DIV 10

pM  pM  .Left

next k

if Over > 0

then NEW(d)

d  .Right  pM  .Right

d  .Left  pM

pM  .Right  .Left  d

pM  .Right  d

M  .Count  M  .Count + 1

d  .Value  Over

endif

Add(AC,M)

ShiftLeft(Y)

pX  pX  .Left

next j

AC  .Sign  NewSign

Clear(Y)

Clear(M)

end {Multiply

Division by repeated subtraction is as slow as multiplication by repeated addition, but the alternative algorithm used by fifth graders is much more complex than repeated subtraction. For contrast with multiplication, a version of repeated subtraction is applied here: the divisor is added to itself until it is larger than the dividend. Each such addition is paired with an increment of the result.

Auxiliary registers are used as they are for multiplication and destroyed on exit from Divide. The initialization is:

procedure Prolog

NewSign  (AC  .Sign = X  .Sign)

AC  .Sign  TRUE

X  .Sign  TRUE

D  AC

NewRegister(AC)

NewRegister(R)

NewRegister(S)

end {Prolog

The resulting divide logic is:

procedure Divide(X)

if X  .Count = 0

then Clear(AC)

return

endif

Prolog

MakeCopy(S,X)

MakeCopy(AC,One)

R  LargerOf(D,S)

while R = D do

Carry(AC,One)

Carry(S,X)

R  LargerOf(D,S)

endwhile

Borrow(AC,One)

AC  .Sign  NewSign

Clear(D)

Clear(S)

end {Divide

A listing of a Pascal program that results from this design follows:

PROGRAM UnBound (InPut,OutPut);

TYPE  Digit =  DigitNode;

Register =  RegisterNode;

DigitNode = RECORD

Value : 0 . . 9;

Left : Digit;

Right : Digit

END;

RegisterNode = RECORD

Sign : BOOLEAN;

Count : INTEGER;

First : Digit;

Last : Digit

END;

VAR  Op ,NextOP : CHAR;

NoX,Done  : BOOLEAN;

One,X,AC  : Register;

OperatorSet : SET OF CHAR;

Numeric  : SET OF CHAR;

{  }

PROCEDURE Display (AC : Register);

VAR pAC : Digit;

k : INTEGER;

BEGIN

Write1n;

pAC := AC  .First;

IF  NOT (AC  . Sign)  THEN Write('-');

FOR  k := 1 TO (AC  . Count + 1) DO BEGIN

Write(pAC  .Value);

pAC := pAC  . Right

END;

Write1n

END {Display};

{  }

PROCEDURE NewRegister(VAR R : Register);

VAR d : Digit;

BEGIN

NEW(d);

d  .Left := d;

d  .Value := 0;

d  .Right := NIL;

NEW(R);

R  .First := d;

R  .Last := d;

R  .Sign := TRUE;

R  .Count := 0

END   {NewRegister};

{  }

PROCEDURE Clear (VAR R : Register);

VAR p , q : Digit;

BEGIN

p := R  .Last;

q := P  .Left;

WHILE (p <> R  .First) DO BEGIN

DISPOSE(p);

p := q;

q := p  .Left

END;

R  .Last := p;

R  .Count := 0;

P  .Right := NIL;

R  .Sign := TRUE

END {Clear};

{  }

PROCEDURE MakeOne(VAR One : Register);

VAR d : Digit;

BEGIN

NewRegister(One);

NEW(d);

d  .Value := 1;

d  .Left := One  .First;

d  .Right := NIL;

One  .First  .Right := d;

One  .Last := d;

One  .Count := 1

END {MakeOne};

{  }

PROCEDURE Preface;

BEGIN

Write1n('This program simulates a calculator that');

Write1n('allows unbounded integers. Enter values');

Write1n('followed by operators. The accepted operators');

Write1n('are: +,-,*,/,=,C (for clear),Q (for quit).');

NewRegister(AC);

NewRegister(X);

MakeOne(One);

Numeric := ['0'..'9'];

OperatorSet := ['+','-','*','/','=','C','Q']

END  {Preface};

{  }

PROCEDURE Compact(VAR R : Register);

VAR p, q, t : Digit;

BEGIN

p := R  .First;

q := p  .Right;

IF  (q  <>  NIL) THEN IF (q  .Value <> 0) THEN q:= NIL;

WHILE   (q <> NIL)  DO BEGIN

t := q  .Right;

DISPOSE(q);

R  .Count := R  .Count - 1;

P  .Right := t;

q := t;

IF (t <> NIL)

THEN BEGIN

t  .Left := p;

IF (t  .Value <> 0) THEN q := NIL

END

END;

IF  (R  .Count = 0) THEN R  .Last := R  .First

END  {Compact};

{  }

PROCEDURE ValueIn(VAR X : Register; VAR NoX : BOOLEAN;

VAR NextOP : CHAR);

VAR  ch : CHAR;

d : Digit;

BEGIN

NoX := TRUE;

Clear(X);

Read(ch);

WHILE NOT (ch IN OperatorSet)

DO BEGIN

IF  (ch IN Numeric)

THEN BEGIN

NoX := FALSE;

NEW(d);

d  .Right := NIL;

d  .Value := ORD(ch) - ORD('0');

d  .Left := X  .Last;

X  .Last  .Right := d;

X  .Last := d;

X  .Count := X  .Count + 1

END;

Read(ch)

END;

NextOp := ch;

Compact(X)

END  {ValueIn};

{  }

FUNCTION LargerOf(AC,X : Register) : Register;

VAR  K : INTEGER;

pAC,pX : Digit;

BEGIN

LargerOf := AC;

IF   (AC  .Count <= X  .Count) THEN

IF     (AC  .Count < X  .Count)

THEN LargerOf := X

ELSE BEGIN

k := AC  .Count;

pAC := AC  .First  .Right;

pX := X  .First  .Right;

WHILE (k > 0) DO

IF (pAC  .Value < = pX  .Value)

THEN IF  (pAC  .Value < pX  .Value)

THEN BEGIN

LargerOf := X;

K := O

END

ELSE BEGIN

pAC := pAC  .Right;

pX := pX  .Right;

k := k - 1

END

ELSE k := O

END;

END  {LargerOf};

{  }

PROCEDURE MakeCopy(VAR M : Register; Y : Register);

VAR  d,pY : Digit;

k : INTEGER;

BEGIN

Clear(M);

IF  (Y  .Count > 0) THEN BEGIN

pY := Y  .First  .Right;

FOR k := 1 TO Y  .Count DO BEGIN

NEW(d);

d  .Right := NIL;

d  .Value := PY  .Value;

pY := pY  .Right;

d  .Left := M  .Last;

M  .Last  .Right := d;

M  .Last := d

END;

M  .Count := Y  .Count;

END

END {MakeCopy};

{  }

PROCEDURE Carry(VAR AC : Register; X : Register);

VAR  pAC, pX, d : Digit;

k,Sum, Over : INTEGER;

BEGIN

pAC := AC  .Last;

pX := X  .Last;

Over := 0;

FOR K := 1 TO AC  .Count DO BEGIN

Sum := pAC  .Value + pX  .Value + Over;

IF  (Sum > 9)

THEN BEGIN

Over := 1;

pAC  .Value := Sum - 10

END

ELSE BEGIN

Over := 0;

pAC  .Value := Sum

END;

pAC := pAC  .Left;

pX := pX  .Left

END;

IF  (Over > 0)

THEN BEGIN

NEW(d);

d  .Right := pAC  .Right;

d  .Left := pAC;

pAC  .Right  .Left := d;

pAC  .Right := d;

d  .Value := Over;

AC  .Count := AC  .Count + 1

END

END {Carry};

{  }

PROCEDURE Borrow(VAR AC: Register; X: Register);

VAR  pAC,pX: Digit;

k,Loan,Difference: INTEGER;

BEGIN

pAC := AC .Last;

pX := X .Last;

Loan := 0;

FOR k := 1 TO AC .Count DO BEGIN

Difference := pAC .Value - pX .Value - Loan;

IF  (Difference < 0)

THEN BEGIN

Loan := 1;

pAC .Value := Difference + 10

END

ELSE BEGIN

Loan := 0;

pAC .Value := Difference

END;

pAC := pAC .Left;

pX := pX .Left

END;

Compact(AC)

END {Borrow};

{  }

PROCEDURE Add(VAR AC: Register; VAR X : Register);

VAR R: Register;

BEGIN                   {X is VAR as AC may swap with it.}

R := LargerOf(AC,X);

IF  (R = X)

THEN BEGIN

X := AC;

AC := R

END;

IF  (X .Count <>0)

THEN IF  (AC .Sign = X .Sign)

THEN Carry(AC,X)

ELSE Borrow(AC,X)

END  {Add};

{  }

PROCEDURE Subtract(VAR AC: Register; VAR X: Register);

BEGIN

X .Sign := NOT X .Sign;

Add(AC,X)

END {Subtract};

{  }

PROCEDURE Multiply (VAR AC: Register; VAR X: Register);

VAR  pM,pX,d: Digit;

M,Y : Register;

v,k,j,Over,Product: INTEGER;

NewSign: BOOLEAN;

{  }

PROCEDURE SetUp;

VAR  R: Register;

BEGIN

Y := AC;

NewRegister(AC);

NewRegister(M);

R := LargerOf( Y,X);

IF  (R = X)

THEN BEGIN

X := Y;

Y := R

END;

NewSign := (Y .Sign = X .Sign);

X .Sign := TRUE;

Y .Sign := TRUE;

Clear(AC)

END {SetUp};

{  }

PROCEDURE ShiftLeft(VAR Y: Register);

VAR  d: Digit;

BEGIN

NEW (d); 

d .Value := 0;

d .Right := NIL;

d .Left := Y .Last;

Y .Count := Y .Count + 1;

Y .Last .Right := d;

Y .Last := d

END {ShiftLeft};

{  }

BEGIN {Multiply}

SetUp;

IF  (X .Count <> 0)

THEN BEGIN

pX := X .Last;

FOR  j := 1 TO X .Count DO BEGIN

Over := 0;

MakeCopy(M,Y);

pM := M .Last;

v := pX .Value;

FOR k := 1 TO M .Count DO BEGIN

Product:=pM .Value* v + Over;

pM .Value := Product MOD 10;

Over := Product DIV 10;

pM := pM .Left

END;

IF  (Over > 0)

THEN BEGIN

NEW (d);

d .Right := pM .Right;

d .Left := pM;

pM .Right .Left := d;

pM .Right := d;

M .Count := M .Count + 1;

d .Value := Over

END;

Add(AC,M);

ShiftLeft(Y);

pX := pX .Left

END;

AC .Sign := NewSign;

Clear(Y);

Clear(M)

END

END  {Multiply};

{  }

PROCEDURE Divide(VAR AC: Register; VAR X: Register);

VAR  NewSign: BOOLEAN;

D,R,S : Register;

{  }

PROCEDURE Prolog;

BEGIN

NewSign := (AC .Sign = X .Sign);

AC .Sign := TRUE;

X .Sign := TRUE;

D := AC;

NewRegister(AC);

NewRegister(R);

NewRegister(S)

END {Prolog};

{  }

BEGIN                    {Divide}

IF  (X .Count = 0)

THEN Clear(AC)

ELSE BEGIN

Prolog;

MakeCopy(S,X);

MakeCopy(AC,One);

R := LargerOf(D,S);

WHILE (R = D) DO BEGIN

Carry(AC,One);

Carry(S,X);

R := LargerOf(D,S)

END;

Borrow(AC,One);

AC .Sign := NewSign;

Clear(D); Clear(S)

END

END  {Divide};

{  }

PROCEDURE Swap;

VAR  R: Register;

BEGIN

R := AC;

AC := X;

X := R

END  {Swap};

{**

**}

BEGIN  {UnBound}

Preface;

Done := FALSE;

Op := 'C';

REPEAT

ValueIn(X,NoX,NextOp);

IF  (NextOp = 'Q')

THEN Done = TRUE

ELSE BEGIN

IF  (NextOp = 'C')

THEN BEGIN

Clear(X); Clear(AC);

Op :='C'

END;

IF  NoX  THEN MakeCopy(X,AC);

CASE  Op  OF

'C' : Swap;    {AC with X}

'=' : Swap;

'+' : Add(AC,X);

'-' : Subtract(AC,X);

'*' : Multiply(AC,X);

'/' : Divide(AC,X)

END

END;

Op := NextOp;

Display(AC)

UNTIL Done

END  {UnBound}.